Mathematics - All About Solving Polynomials (part 1)

Introduction
Hey it's a me again @drifter1!
Today's article is another high-school refresher on Mathematics, and more specifically on Solving Polynomials. It's a follow-up to the previous posts about Polynomial Arithmetic, Rational Expressions and Simplifying Expressions. Because the topic came out more complicated than expected, it will be split into various parts.
So, without further ado, let's get straight into it!
Factors = Roots
Solving an equation is always about finding values for the variable (or variables) for which the equation equals zero. These values are called roots or zeroes. In the context of polynomials those roots can be written as factors of the form (x - r), where r is the root. So, solving a polynomial can be thought of as both:
- Solving (finding the roots or zeroes) the polynomial equation p(x) = 0
- Factoring the polynomial p(x)
In other words, every root can be turned into a factor, and vice versa, which is known as the Factor Theorem.
Solution
As the degree of the polynomial increases, solving becomes more and more complicated as well. Finding the solution of linear polynomials requires simple algebra. Finding the roots of quadratic poolynomials is also straight-forward, as the so called Quadratic Formula can be used to solve them quite quickly. There are also formulas for cubic and quartic polynomials, of degree 3 and 4 respectively, which have time-consuming calculations though. As the degree increases even further, the problem becomes harder and harder. And that's where factoring, which reduces the degree by at least 1, comes into play.
In general, the solution will be either exact (also called analytic) or approximate (also called numeric). What was explained in the previous paragraph is basically the analytic method. Approximation is mostly used when finding that exact solution is basically impossible.
Solving Procedure - Steps
Let's get more in-depth into the analytic solving procedure.
The procedure can be split into the following steps:
- Put the polynomial into Standard Form and apply basic Simplification techniques.
- Identify or predict the possible amount and types of roots expected.
- Solve the linear and quadratic polynomial equations (degree 1 or 2) that come up.
- Find a rational factor or root by applying various techniques.
- Divide by the factor in order to reduce the degree of the polynomial, and continue with step 3 on that reduced polynomial.
- If no root can be found apply numeric methods
- After solving, write down the roots or the polynomial in factorized form.
At any stage of the procedure it's possible to use the cubic or quartic formulas, for polynomials of degree 3 or 4 respectively, instead of factoring. But, because the formulas are quite complicated factoring is mostly preferred.
Pre-Processing the Polynomial Equation
Before getting into solving, the polynomial equation should be put into Standard Form and simplified as needed by taking common factors, making sure all coefficients are integers and not fractions etc. It's a quite simple step that tends to be forgotten, but makes the rest of the procedure easier.
Standard Form
Standard Form is about putting the polynomial in decreasing order of exponents, and with all terms in one side and a zero in the other side of the equation, leading into an equation of the form p(x) = 0.
For example:

Common Factors
The simplest type of common factor is -1, which is taken in order to have a positive coefficient for the highest exponent, as shown in the example below.
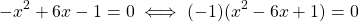
The common factor can also be any constant integer, which is taken for the sake of dividing the coefficient of all terms in the polynomial, in order to make them smaller, like in the example below.
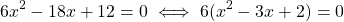
This example also is a best case scenario, where the highest exponent now has an coefficient of 1. In general, the highest exponent (and all terms in general) should end up with the smallest possible coefficient.
When there are fractions as coefficients those should be turned into integer coefficients. In these cases, the common factor may be a fraction as well. To get more specific, such a common factor will be a fraction of the form 1 divided by the lowest common denominator.
For example:

If the problem is about solving an equation, then throwing away any common factor is allowed, as the roots are the same. But when factoring a polynomial, these common factors need to be kept, in order to end up with a factorized polynomial which is identical to the original polynomial.
Amount and Types of Roots
The Fundamental Theorem of Algebra states that a polynomial of degree n will have n roots, some of which can be multiple roots. Combining this with the Factor Theorem, tells us that any polynomial can be factorized in the following way:
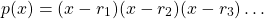
where ri are the roots of the polynomial equation, and some of even all of them can be equal (multiple roots). It's thus possible to have factors of the form (x - ri )2.
Complex and Irrational Roots
Of course, any of these roots can be complex roots, which come in conjugate pairs. I doesn't matter if the polynomial has only real coefficients, either of the roots can be real or complex.
Similarly, even if the polynomial has only rational coefficients, there might be irrational roots, which also come in conjugate pairs.
Descartes' Rule of Signs
When trying to decide the types of roots to pursue, a useful rule to apply is Descartes' Rule of Signs. The rule is based on the concept of variation in sign. The amount of sign variations is calculated in a polynomial that is arranged in standard form. A sign variation occurs if the sign of a coefficient is different from the preceding coefficient. Zero coefficients are ignored.
Knowing the number of variations in the polynomial p(x) and p(-x) allows us to predict the number of positive, negative and complex roots, in the following way:
- The number of positive roots is equal to the number of sign variations in p(x), or less than that by an even number (multiple of 2).
- The number of negative roots is equal to the number of sign variations in p(-x), or less than that by an even number (multiple of 2).
Consider the following polynomial, for example:

There are 2 sign variations in p(x), and thus the number of positive solutions is either 2 or 0.
The polynomial p(-x) is equal to:

and has 2 sign variations as well, which means that the number of negative solutions is either 2 or 0.
Because the degree is 4 the total number of roots is 4, and thus based on that rule the possible roots will be either:
| Positive | Negative | Complex |
|---|---|---|
| 2 | 2 | 0 |
| 2 | 0 | 2 |
| 0 | 2 | 2 |
| 0 | 0 | 4 |
In the case of this polynomial, the roots are -7, -1, 1 and 2, which was the first prediction.
Of course, if either of the positive or negative roots in those predictions where non-zero (even a 1 in the whole column) in all predictions, then these types of roots would be solved for first, as they will occur for sure.
RESOURCES:
References
- https://www.mathsisfun.com/algebra/polynomials-solving.html
- https://www.khanacademy.org/math/algebra-home/alg-polynomials
- https://brownmath.com/alge/polysol.htm
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Final words | Next up
And this is actually it for today's post!
The remaining parts will be posted in the following days...
The next "All About" article will be about:
- Exponentials and Logarithms
Basically more High-School Math Refreshers!
See ya!

Keep on drifting!
Posted with STEMGeeks
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (80% of the curation rewards are returned).
Please consider including @stemsocial as a beneficiary to get a stronger support.