Mathematics - All About Polynomial Arithmetic

Introduction
Hey it's a me again @drifter1!
Today's article is another high-school refresher on Mathematics, and more specifically on Polynomial Arithmetic. All will be covered in this single All About post.
Division will be skipped today, and be explained in a follow-up article, where we will talk about Rational Expressions only!
So, without further ado, let's get straight into it!
Polynomials
The term Polynomial comes from poly- (many) and -nomial (terms), and thus basically means many terms. It can contain constants, variables and exponents (with natural exponent like 0, 1, 2, ...), but no division by variable. Single-variable polynomials yield smooth curves. Having more than one variable leads to more complicated shapes.
For example, the following is a valid polynomial:
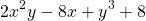
whilst the following examples are not:
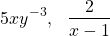
because:
- the first contains a negative exponent (-3)
- the second is a rational expression, and no division by variable is allowed.
Division by constants and irrational constants are allowed though! So, terms such as:
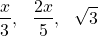
can be parts of a polynomial, or a polynomial themselves.
Special Names
The polynomials with 1, 2 or 3 terms are given special names:
- Monomial : 1 term
- Binomial : 2 terms
- Trinomial : 3 terms
Degree
For a polynomial with only one variable, the degree it the largest exponent of that variable.
For example:

has a degree of 4.
Standard Form
Its common to write a polynomial putting the terms of highest degree (exponent) first. This form is known as the Standard Form.
A single-variable n-degree polynomial can thus be generalized as follows:
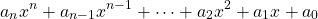
where some of the ai constant coefficients are allowed to be zero, eliminating the term completely. The absence of any degree can thus be thought of as having a coefficient of zero.
The previous example can therefore be expressed as follows:
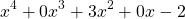
Polynomial Addition and Subtraction
When adding (or subtracting) polynomials, like terms are summmed together, which basically means that the constant coefficients are summed. Of course, the result is again a valid polynomial!
Like Terms
Like terms are terms with the same variables and exponents on those variables.
For example, the following are like terms:
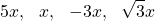
because all have the variable x and exponent 1.
Similarly, the following are like terms as well:
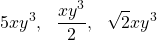
because they all have xy3.
The following are not like terms:
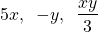
Adding Polynomials
So, adding a polynomial is basically a two step procedure:
- Identify the like terms
- Add the like terms together
For example:
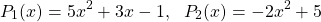
are added as follows:
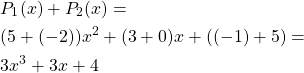
Subtracting Polynomials
Subtraction is basically addition with inverted signs. Thus, we can invert the signs of each term of the polynomial with the minus sign in front, and then add as usual.
For example, the polynomials of the previous can be subtracted as follows:
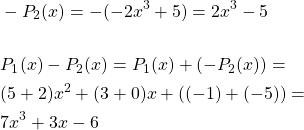
Polynomial Multiplication
Similar to addition, the result of multiplying two or more polynomials together is again a polynomial. But, this procedure is a little more time-consuming.
More specifically, when multiplying two polynomials:
- we multiply each term in one polynomial by each term in the other polynomial
- sum the like terms together, and simplify as needed
Let's slowly increase the difficulty, starting off with the multiplication of two monomials...
Monomial times Monomial
When multplying two monomials (one term by one term), we just have two multiply the constants and each variable together. For example, x with x to yield x2, or x and y together to yield xy, as shown in the following example:

Monomial times Binomial (or the opposite)
When multiplying a monomial by a binomial, we have to multiply the single term of the monomial by each of the two terms of the binomial.
For example:
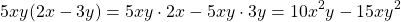
Binomial times Binomial
When multiplying two binomials, we multiply each of the two terms in the first binomial by each of the other two terms in the second binomial. In total 4 multiplications, followed by simplifying.
It's easy to think of it as simple Algebra:
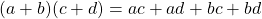
but with the result of that multiplication to be a little more special.
For example:
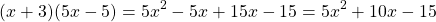
In this example the like terms -5x and 15x where added together in order to yield 10x, which simplifies the polynomial, and puts it into standard form.
Special Products
Getting into more complicated cases is uncessary I think...But, let's cover some special products, which can be used as formulas.
Difference of Squares
The following equality is known as the difference of squares:
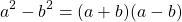
Identifying it may allow faster simplifications!
Square Formulas
Similarly, the following two equalities, are also used as formulas quite a lot in mathematics:
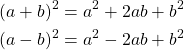
RESOURCES:
References
- https://www.mathsisfun.com/algebra/polynomials.html
- https://www.khanacademy.org/math/algebra2/x2ec2f6f830c9fb89:poly-arithmetic
- http://mathcenter.oxford.emory.edu/site/math100/polynomialArithmetic/
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Final words | Next up
And this is actually it for today's post!
The next "All About" articles will be about:
- Rational Expressions
- Simplifying and Factoring Expressions
- Exponentials and Logarithms
Basically more High-School Math Refreshers!
See ya!

Keep on drifting!