Mathematics - All About Geometry (Part 6)
[Image1]
Introduction
Hey it's a me again @drifter1!
This is the sixth and final part of my high-school refresher series on Geometry. I highly suggest checking out part1, part2, part3, part4 and part5 before this part.
So, without further ado, let's get straight into it!
Analytic Geometry Basics
A point in the Cartesian Coordinate System, the so called x-y plane, is denoted as (x1, y1). This doesn't represent an open interval of numbers of the form (a, b), which is commonly used in mathematics, but a point in this x-y plane. We covered the system more thoroughly in part 3. This is the basis of Analytical Geometry, where mathematical equations are used in order to represent shapes and their relation.
Delta notion
Let's start simple. Considering two points A and B in this x-y plane, moving from point A to B there will be a change in the x and/or y coordinates. This change is called a delta, Δ (capital Greek alphabet delta). Δx is the change in x, whilst Δy the change in y.
For example, if A = (3, 1) and B = (2, 3) then moving from A to B yields:
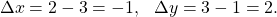
The general formulas for points (x1, y1) and (x2, y2) are:
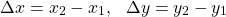
Slope
Having two distinct points A and B, only one straight line can be drawn that passes through both points. This line has a slope equal to the ratio of Δy and Δx or:
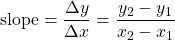
For the previous example, we have:

Straight Line
The simplest straight line equation (the slope-intersept equation) is:
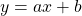
where a is the slope.
This equation is basically the result of refactoring the slope equation and entering any point that's on the line, such as:
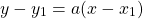
This is the so called point-slope equation of a straight line.
For example, in the previous example, entering either of the two points results in the same line, which is:
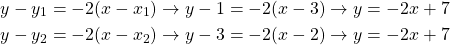
The more general formula of a straight line is:
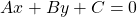
where A, B and C are constants, and A, B are not both 0.
Any y = b line is a horizontal line, whilst any x = a line is a vertical line.
Axes Intersection Points
To find the y value for a specific x value we simply input x into the equation and solve for y (the opposite for finding x). Thus, in order to find where the line intersects the x-axis we set y = 0 and to find where the line intersects the y-axis we set x = 0. Simple stuff.
For example, for the previous line x = 0 and y = 0 yield the following intersection points:

Parallel Lines
Two lines are parallel to each other if the slopes are equal.
For example:
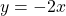
is a line parallel to the previous example's line.
Perpendicular Lines
Two lines are parallel if their slopes are negative reciprocales:
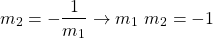
For example:
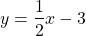
is a line perpendicular to the previous example's line as:

Line Intersection Point
In order to find where two or more lines meet (if they meet) their linear system needs to be solved which is a topic covered by Linear Algebra.
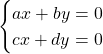
For example:
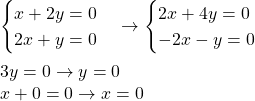
Distance Between 2 Points
The distance between two points (x1, y1) and (x2, y2) is a direct consequence of Pythagoras's Theorem and equal to:
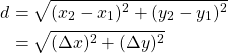
For example, the distance between the points A and B from before is:
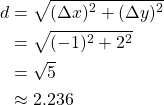
Midpoints
Considering the line segment which joins two points (x1, y1) and (x2, y2), the midpoint of this segment is at:
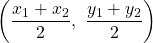
Conics
The simplest non-straight lines are the conics covered by the end of part 4.
Their general equation is of the form:
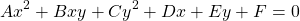
The Bxy term is about conic rotation. The Dx, Ey and F terms affect the vertex and center points. And lastly, for A, C we have the following shapes:
- A = C : Circle
- AC > 0 (A ≠ C) : Ellipse
- AC = 0 : Parabola
- AC < 0 : Hyperbola
For example, a circle with center at (2, -2) and radius of 2, has the following equation:
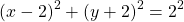
which can also be expanded into the general equation format:
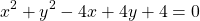
These are all topics of the branch of mathematics known as Mathematical Analysis, which also deals with topics such as limits, differentiation, integration, sequences, series etc.
RESOURCES:
References
- https://www.khanacademy.org/math/geometry-home
- https://www.sfu.ca/math-coursenotes/Math%20157%20Course%20Notes/sec_AnalyticGeometry.html
Images
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Final words | Next up
And this is actually it for today's post and this small refresher series!
The next "All About" articles will be about:
- Polynomial Arithmetic
- Exponentials and Logarithms
- Rational Expressions
Basically more High-School Math Refreshers!
See ya!

Keep on drifting!