Mathematics - All About Geometry (Part 4)
[Image1]
Introduction
Hey it's a me again @drifter1!
This is the fourth part of my high-school refresher series on Geometry.
I suggest checking out part1, part2 and part3 before this.
So, without further ado, let's get straight into it!
Circle Theorems
The properties of the circle lead to some interesting, mainly angle-related theorems.
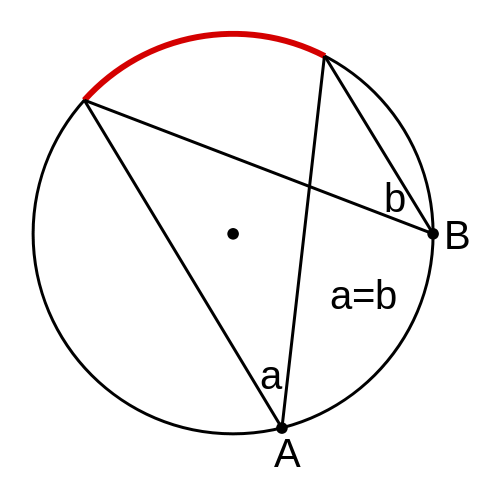
Inscribed Angles subtended by same Arc
The angle that is made from points sitting on the circle's circumference is called an Inscribed Angle. Keeping the same end points and moving the middle (apex) point, doesn't affect the angle, if those points are within the remaining circumference of the circle.
Consider the figure below. In this figure the apex points A and B form the angles a and b, which are equal because they are subtended by the same arc (the red one).
[Image 2]
Angles at the Center and at the Circumference
In addition to the previous theorem, the inscribed angle and the angle made from the center towards the end points are also related, in the following way:
The center angle is twice the inscribed angle if both have the same end points and are within the same arc.
For example, this applies for the ABC - AOC pair shown below:
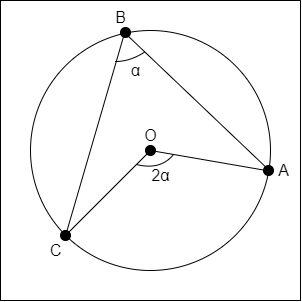
Moving point B along the upper AC arc doesn't affect the angle, as well as the relation between the angles.
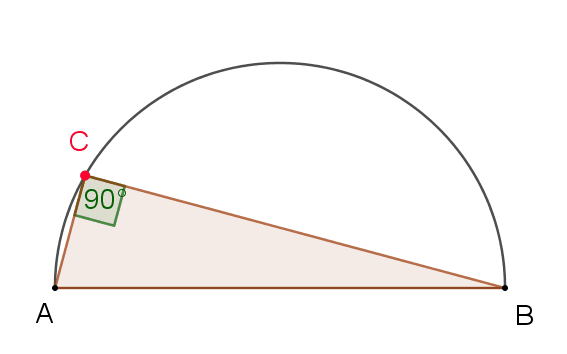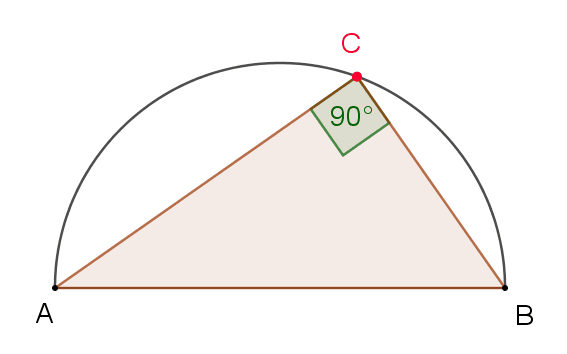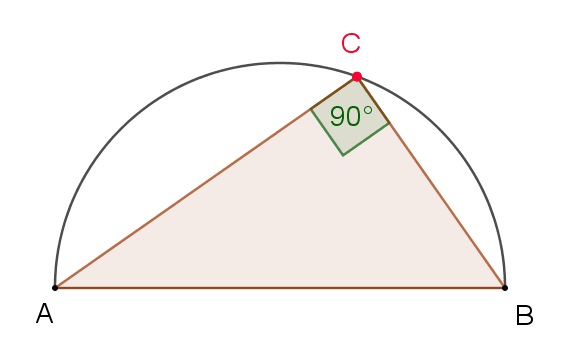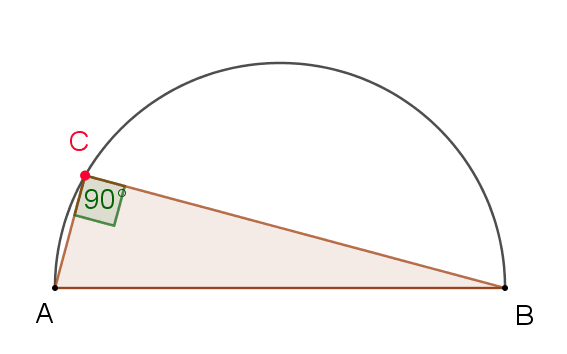
Angle in a Semicircle (Thales' Theorem)
A special case of the previous theorem is Thales' Theorem, which tells us that an inscribed angle across a circle's diameter is always a right angle. In other words, the inscribed angle formed by the endpoints of a circle's diameter is always the same, anywhere on the circumference, and always equal to 90°, because the center angle will be 180° (line) for both sides of the semicircle.
[Image 3]
Opposite Angles in a Cyclic Quadrilateral
A Cyclic Quadrilateral is a quadrilateral with all it's vertices on a circle's circumference. The opposite angles in such a quadrilateral have the special property of always adding up to 180°.
For example, in the figure below, α + γ = 180°, and β + δ = 180°:
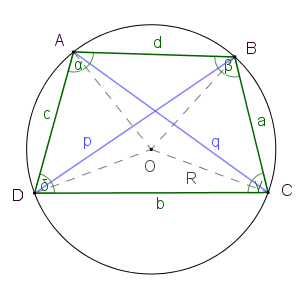
[Image 4]
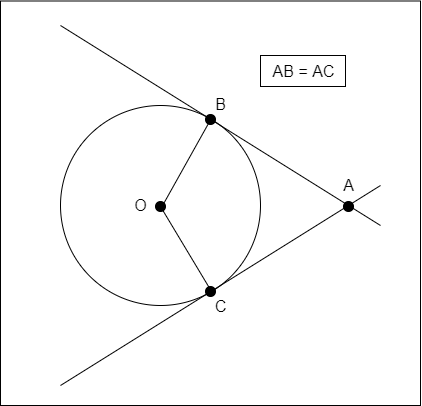
Lengths of Tangents from a Point to a Circle are Equal
From a point outside a circle two tangent lines (or tangents) can be drawn. The distance from that point towards the points of contact is the same in both cases.
For example, if A is a point outside a circle, and B and C are the points of contact of the two tangents, then the line segments AB and AC will have equal length, as shown below.
Angle between a Tangent and a Circle's Radius
As a continuation of the previous theorem, what are the angles ABO and ACO, if OB and OC are both equal to the radius? Well, the angle between a tangent and a radius of a circle is always exactly 90°. In other words, a tangent line and the radius which can be drawn from the center towards the point of contact of the tangent line are perpendicular to each other.
Alternate Segment Theorem
The Alternate Segment Theorem states:
For any circle, the angle between a tangent and a chord through the point of contact of the tangent is equal to the angle made by the chord in the alternate segment.
Visually, it's easier to understand it. So, explain the figure below.
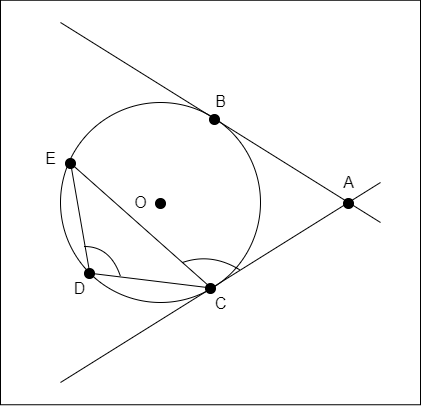
In this figure, the angles ACE and CDE are equal. The angles will also be equal if Point E is moved along the circumference, but stays in the segment opposite to the tangent.
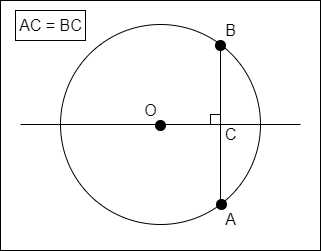
Perpendicular from Center Bisects Chord
A line which passes through the center, and is perpendicular to a chord, bisects that coord (splits it into two equal parts), as shown below.
Conic Sections
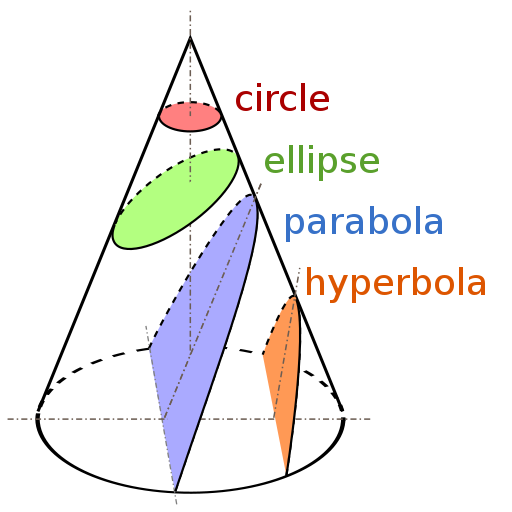
Taking different slices through a cone, one can create circles, ellipses, parabolas and hyperbolas. All these shapes are thus related and called conic sections.
[Image 5]
- Circle : created by cutting straight through a cone
- Ellipse : created by cutting a cone in a slight angle
- Parabola : created by cutting parallel to an edge of a cone
- Hyperbola : created by cutting a cone in a steep angle
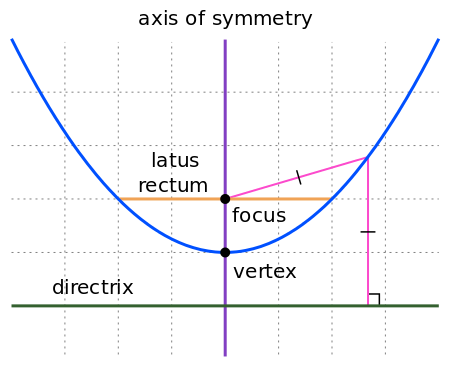
Focus and Directrix
Conic sections can be defined using a straight line and a point, which are called directrix and focus. In the special case of an ellipse there are two focus points, called foci and two directrix lines, one on each side. When measuring the distance from the focus to a point on the curve, and perpendicular from the directrix to that point, the two distances always have the same ratio:
- For a circle the ratio is 0, because the directrix is a tangent of the circle, thus having a distance of 0 towards any point on the circumference of the circle
- For an ellipse the ratio is less than 1
- For a parabola the ratio is exactly equal to 1
- For a hyperbola the ratio is greater than 1
The figure below shows the definition of a parabola.
[Image 6]
Eccentricity
The ratio mentioned previously is a property called Eccentricity. For any conic section the points on the curve have a distance to the focus which is equal to the eccentricity times the distance to the directrix. Therefore:
- Circle : eccentricity = 0
- Ellipse : 0 < eccentricity < 1
- Parabola : eccentricity = 1
- Hyperbola : eccentricity > 1
So, eccentricity basically shows us how "un-circular" a curve is. The higher the number the less the curvature. Of course, a straight line has an eccentricity of infinity.
Vertex and Focal Length
A line from the focus point towards the directrix, which is perpendicular to the directrix, cuts the curve at a specific point, which is called a vertex. The distance from the focus point to the vertex is the focal length of the conic section.
Latus Rectum
The latus rectum (latin for "side" and "straight") is a line parallel to the directrix which passes through the focus. Depending on the shape its length is:
- Parabola : four times the focal length
- Circle : equal to the circle's diameter (or twice the radius)
- Ellipse : equal to 2b²/a, where a and b are half the major (or transverse) and minor (or conjugate) diameter
- Hyperbola : equal to 2b²/4a, where a and b are half the diameter of the transverse and conjugate axis respectively.
To understand this better, the axes of an ellipse, as well as the distances a and b are shown below. F1 and F2 are the foci of the eclipse, and C its center.

[Image 7]
Equations
When placing these shapes on the Cartesian Coordinate System with the center at O (0,0), the equations that define all but the parabola are as follows:

The circle is basically a "special" case of the ellipse where a = b = r.
There also exists a General Equation, which covers all of these plane curves, which is:
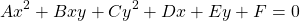
Using only x and y, even with factors, will only yield straight lines. Thus, at least one square of them (x², y²) or the combined xy needs to have a non-zero factor.
A simple example of a parabola is the quadratic function y = x², with the following plot:
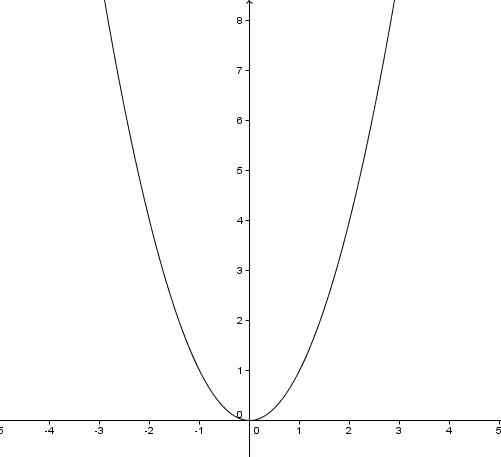
[Image 8]
RESOURCES:
References
- https://www.khanacademy.org/math/geometry-home
- https://www.mathsisfun.com/geometry/
- https://www.splashlearn.com/math-vocabulary/topics/geometry--4
- http://www.timdevereux.co.uk/maths/geompages/8theorem.php
- https://www.cuemath.com/geometry/alternate-segment-theorem/
- https://www.vedantu.com/maths/latus-rectum
Images
- https://pixabay.com/vectors/geometry-compasses-dividers-155184/
- https://commons.wikimedia.org/wiki/File:Subtended_-Arc_of_circle_subtended_by_two_angles.svg
- https://commons.wikimedia.org/wiki/File:Thales_kreis_animation.gif
- https://commons.wikimedia.org/wiki/File:ABCD_-_cyclic_quadrilateral.png
- https://commons.wikimedia.org/wiki/File:Conic_Sections.svg
- https://commons.wikimedia.org/wiki/File:Parts_of_Parabola.svg
- https://commons.wikimedia.org/wiki/File:Ellipse_semi-major_and_minor_axes.svg
- https://commons.wikimedia.org/wiki/File:Y%3Dx%5E2.png
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Final words | Next up
And this is actually it for today's post!
Next time we will get into Solid Geometry...
Also, currently, other ideas for "All About" articles that I have in mind include:
- Polynomial Arithmetic
- Exponentials and Logarithms
- Rational Expressions
Basically more High-School Math Refreshers!
See ya!

Keep on drifting!
Electronic-terrorism, voice to skull and neuro monitoring on Hive and Steem. You can ignore this, but your going to wish you didnt soon. This is happening whether you believe it or not. https://ecency.com/fyrstikken/@fairandbalanced/i-am-the-only-motherfucker-on-the-internet-pointing-to-a-direct-source-for-voice-to-skull-electronic-terrorism
This is definitely what you call a good refresher! Kudos! Are you a teacher by profession or you just love math?
Hey @indayclara ,
I'm a Computer Science student, currently going for a master's degree. But, I enjoy teaching, which is why I upload these programming, physics and mathematics related posts. I'm not yet sure about which direction to take as a career! Teaching at universities or serious courses on websites like Udemy is a high possibility though. I don't know, I just keep going...and see where it takes me! 😄
Glad you enjoyed this post!
Best Regards,
@drifter1
Wow! That is dope! I do hope you get to finish your master's degree. Based on your "favorite" subjects, it tells me you are a logical and analytical guy. 😁.
Yes! When in doubt, just let things flow. In the end, life will lead you to your purpose!