Mathematics - All About Geometry (Part 2)
[Image1]
Introduction
Hey it's a me again @drifter1!
This is the second part of my high-school refresher series on Geometry.
I highly suggest reading part1 before this.
So, without further ado, let's get straight into it!
Lines
We already covered a lot about lines in the first part. But, let's get even more specific into how they are named and related to each other, as shown in the figure below.

First of all, what is a line? In geometry, when talking about a line we always mean a straight line, a line with no curvature.
This line can be extended indefinitely in both directions and has negligible width and depth. In addition to the main line definition, we also give parts of the line specific names. For example. a segment is a part of the line enclosed in two points, and a ray start from one point and extends to infinity.
If two lines never intersect with each other they are called parallel, otherwise they are non-parallel. In the special case where the intersection of the lines forms a right angle (90°) the lines are called perpendicular.
Golden Ratio
In mathematics, whenever the ratio of two quantities is the same as the ratio of their sum to the larger of the two quantities, then these two quantities are in a golden ratio, which is always equal to the irrational number φ = 1.618... .
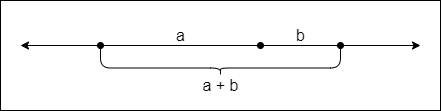
For example, using line segments, if segment a is bigger than segment b then:
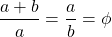
Of course this is not true for all values.
Angles
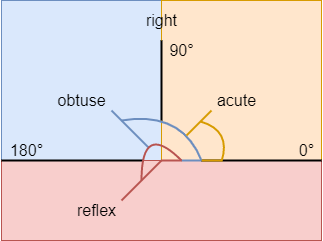
As an angle increases (in degrees or radians) its name changes as well, leading to the following naming conventions:
- Acute angle : Less than 90°
- Right angle : Exactly 90°
- Obtuse angle : Greater than 90° but less than 180°
- Straight angle : Exactly 180°
- Reflex angle : Greater than 180°
- Full rotation : Exactly 360°
Depending on the direction towards the angle is measured the angle is named:
- Positive angle : counterclockwise direction
- Negative angle : clockwise direction
Naming
Angles are mostly given lower-case letters, which sometimes are Greek letters such as a or θ. It's also possible to define the angle by three letters. Where the order of the letters specifies the parts of the angle: the two arms and the vertex in the middle.
For example, in the following figure:
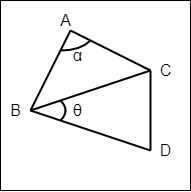
- angle a can be named BAC or CAB (depending on the direction), and
- angle θ can be named CBD or DBC
Angle Pairs
A pair of angles is also given a special name in the following cases:
- Adjacent : the angles are next to each other (share a side)
- Complementary : the sum of the angles adds up to 90°
- Supplementary : the sum of the angles adds up to 180°
- Vertical : the angles are across from each other (made by two intersecting lines)
For example:
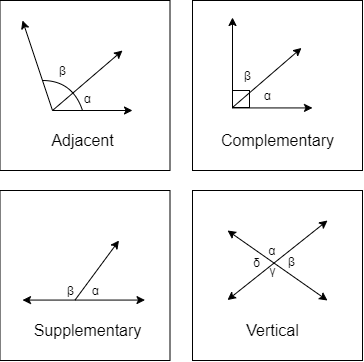
In the last box, the corresponding pairs α, γ, and β, δ are vertical.
Transformations
Transformations are specific actions that can be applied on an shape that don't change it's size, area, angles and line lengths (they lead to so called congruent shapes). Those are:
- Rotation : Turn a shape about a central axis
- Reflection : Flip a shape in respect to a symmetry axis
- Translation : Move a shape around
For example:
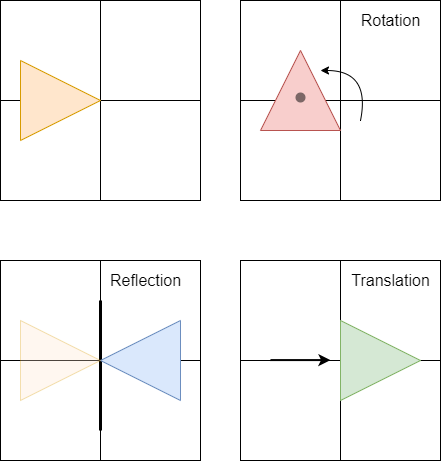
Symmetry
Symmetry is derived from Greek: σύν- (together) and μέτρον (measure), and in the context of Geometry it can be thought of as an agreement in dimensions, an arrangement.
There are three main types of symmetry:
- Reflection (or Line, or Mirror) Symmetry : One half of a shape is the reflection of the other half for a specific line of symmetry.
- Rotational (or Radial) Symmetry : A shape which looks the same after some rotation is applied. The number of possible orientations is called an order.
- Point Symmetry : A shape where for each part there is a matching part with the same distance towards a central point, but in the opposite direction.
Let's get into some examples of each...
Reflection Symmetry
It's easy to find Lines of Symmetry in most of the common shapes, such as:
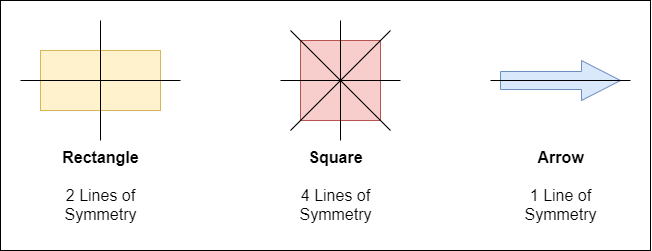
Rotational Symmetry
The Rectangle and Square are also good examples of Rotational Symmetry, with order 2 and 4 correspondingly.
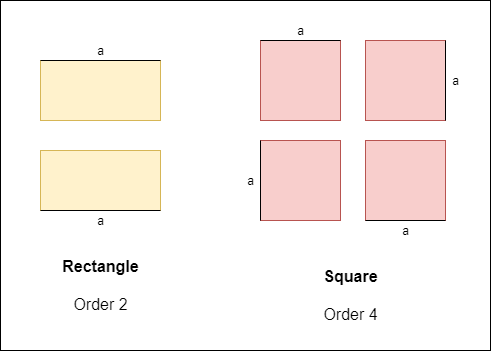
Notice how side a changes places, but leads to the shape overall shape. As such the rotation by 180° in the first case, and by 90° in the second case leads to congruent shapes.
Point Symmetry
Playing Cards often have Point Symmetry, which makes them look the same from the top or bottom. And, let's also not forget to mention latin alphabet letters such as X, H, I, S, N and Z, which have Point symmetry in the center as well.
Congruence vs Similarity
In the previous sections we saw how transformations such as rotation, reflection and/or translation lead to congruent shapes. Congruence basically means equal or agreement. After turning, fliping and sliding around a shape it should be "placable" on top of another shape for them to be congruent.
If in addition to such actions, there's also the need to resize the shape, then the shapes are known as similar. In the case of similar shapes the corresponding angles are equal and the lines are proportional.
For example consider the following triangles:

A and B are congruent, because they can be placed on top of each other after a rotation by 90° and a "slide" towards the other shape.
On the other hand, A, B and C are similar shapes, as a resize is needed before actions such as rotation, reflection and/or translation can be taken.
RESOURCES:
References
- https://www.khanacademy.org/math/geometry-home
- https://www.mathsisfun.com/geometry/
- https://www.splashlearn.com/math-vocabulary/topics/geometry--4
Images
Mathematical equations used in this article, where made using quicklatex.
Block diagrams and other visualizations were made using draw.io
Final words | Next up
And this is actually it for today's post!
Next time we will continue with part 3.
Also, currently, other ideas for "All About" articles that I have in mind include:
- Polynomial Arithmetic
- Exponentials and Logarithms
- Rational Expressions
Basically more High-School Math Refreshers!
See ya!

Keep on drifting!