Triangular Numbers
Hi there. In this mathematics post, I talk about triangular numbers. This topic belongs to patterning section in mathematics. This is one of my more technical math posts as there is a bit of algebra and math notation.

Quicklatex.com is used for the Latex math rendering.
Topics
- Defining Number Sequences
- The Pattern For Triangular Numbers
- Finding The k-th Triangular Number
- Sum Of Triangular Numbers
- Examples
Defining Number Sequences
A sequence of numbers refers to a list of numbers that follow in a pattern. The sequence of numbers can be increasing where the numbers are increasing from one number to the next. Sequences can also be decreasing where the number gets smaller or more negative. Some sequences can be flat where there is no change in the number. Some sequences may not follow a noticeable pattern.
Example One - Increasing Sequence
An increasing sequence of numbers is where the sequence of numbers increases from left to right.
10, 15, 20, 25, 30, 35, 40
Example Two - Decreasing Sequence
A sequences can contain numbers that are decreasing in value such as:
100, 0, -100, -200, -300, -400
Example Three - Flat Sequence
There are sequences that are just flat. No increase nor decrease occurs. This sequence is also called a constant sequence.
1, 1, 1, 1, 1, ...
Example Four - Alternating Sequence
Some funky looking sequences can alternate their signs such as -1 , +1, -1, +1, -1, +1, ....
There are other sequences as well. An arithmetic sequence such as 1, 5, 9, 13, ... has a common difference of 4 as we add up by 4. A geometric sequence such as 1, 2, 4, 8, 16, 32, ... has a common ratio of 2 where we multiply by 2 to obtain the next number.
A finite sequence contains a starting number and an ending number. Infinite sequences contain a starting a number but not ending number as it never ends as indicated by the 3 dots.
The Pattern For Triangular Numbers
The number sequence for triangular numbers is as follows:
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, ...
In diagram form, you can have dots arranged in a triangular fashion. Only the first triangular number of 1 is not shaped like a triangle. Refer to the screenshot (used Autodraw) below.
Finding The k-th Triangular Number
There are a couple of ways of finding the k-th triangular number (where k is a positive whole number above 1). The first way uses dots in diagrams and uses the area formula as found in the MathIsFun website.
The second way is more of an algebraic way of doing it which uses a table of values and finding a quadratic equation. It is technical with the algebra. I present that here.
| Term Number | Triangular Number |
|---|---|
| 1 | 1 |
| 2 | 3 |
| 3 | 6 |
| 4 | 10 |
| 5 | 15 |
| 6 | 21 |
| 7 | 28 |
| 8 | 36 |
| 9 | 45 |
From the table of values, we can find the first differences and the second differences.
| Term Number | Triangular Number | First Difference | Second Difference |
|---|---|---|---|
| 1 | 1 | N/A | N/A |
| 2 | 3 | +2 | N/A |
| 3 | 6 | +3 | +1 |
| 4 | 10 | +4 | +1 |
| 5 | 15 | +5 | +1 |
| 6 | 21 | +6 | +1 |
| 7 | 28 | +7 | +1 |
| 8 | 36 | +8 | +1 |
| 9 | 45 | +9 | +1 |
The first differences is not the same but it is increasing. From the second differences, we have a constant +1. Half of the second difference gives the coefficient of a from the quadratic equation  . This value for
. This value for a is one half.
For finding the values of b and c, a system of two equations needs to be set up. I use x = 1 with f(1) = 1 in the first equation and x = 2 with f(2) = 3 for the second equation.
First Equation

Second Equation
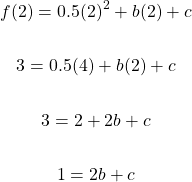
Solving The System Of Equations
From equation one, the variable b can be isolated to obtain b = 0.5 - c. This can be substituted into equation two.
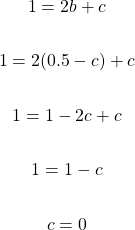
The value of c is 0. Using this value of c in 0.5 = b + c will help in obtaining b = 0.5.
Given a term number we have a quadratic equation for the n-th triangular number:
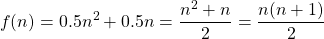
Sum Of Triangular Numbers
This section requires knowledge of series for adding numbers from a sequence.
Everything so far dealt with the sequence of triangular numbers. What if we wanted a (partial) sum of triangular numbers? We would need to utilize series for sums.
Preliminary Concepts
Sum notation is a compact way of representing a sequence of numbers being added together. The ones that are being used are:
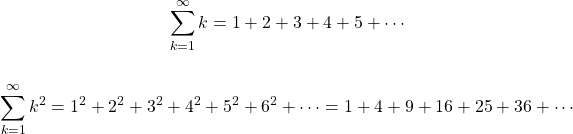
If the sum is multiplied by a number such as 2, each number in the can be multiplied by the multiple. In this example below, I have 2 times the infinite sum. This is the same as multiplying each number in the infinite sum by 2.
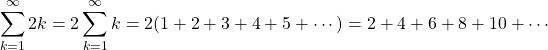
For this section, we focus on finite sums where the sequence does end at the n-th number. The formulas of interest are:

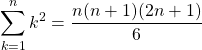
Note that k = 1 index at the bottom means to substitute k with 1 for the first number term and n for the last number term. Not all sums start with a starting index of 1. A different index such as i or j may be used.
Determining The Sum Of k Triangular Numbers
The k-th triangular number is given by:
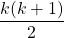
We can represent the sum of triangular numbers such as 1 + 3 + 6 + 10 + 15 + 21 + 28 + 36 + 45 + 55 + 66 + 78 where 78 is the last (or n-th) triangular number. The representation in mathematical notation would be:
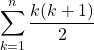
This is equal to:

The formulas from the previous section is applied for the sums.
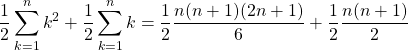
Common factor out one quarter, n and (n + 1).

Some more simplifying with factoring and reducing fractions.

Let's do a quick recap:
The k-th triangular number is given by:
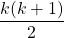
The sum of the first n triangular numbers (1, 3, 6, 10, 15, 21, 28, 36, 45, 55, ..., n) is given by this formula:


Examples
Here are some examples for the n-th triangular number and for the sum of triangular numbers.
Example One
What is the 50th triangular number?
Using n = 50, the 50th triangular number can be found with the formula:
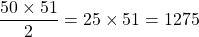
Example Two
Determine the total of the first 100 triangular numbers.
Use the formula with n = 100 for the sum of the first 100 triangular numbers
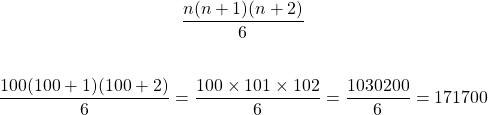
Example Three
What is the total of the fifth triangular number to the tenth triangular number?
The strategy here is is to find the total of the first ten triangular numbers. Afterwards, determine the total of the first four triangular numbers. To obtain the desired sum, do total from first to tenth minus the total from first to fourth.

As a reference, the fifth to tenth triangular numbers are 15, 21, 28, 36, 45 and 55. They do add up to 200.
References:
- https://www.mathsisfun.com/algebra/partial-sums.html
- https://math.stackexchange.com/questions/2435816/a-formula-for-the-sum-of-the-triangular-numbers
Posted with STEMGeeks
