Statistics - Skewness
Statistics - Skewness
Hi there. In this post, I want to talk about the concept of skewness from probability and statistics. The concepts of mean, variance and standard deviation are known but I find that skewness gets overlooked a little bit. Maybe people don't remember/know skewness or find it difficult or something.
Topics
- What Is Skewness?
- Left-Skew Vs Right-Skew
- Calculating Skewness
- The Normal Distribution Is Symmetric
- Skewness In Finance
- Using Software/Programming To Compute Skewness
What Is Skewness?
Skewness refers to the lack of symmetry in numeric data values. As much as we would like symmetric numeric data, a lot of data contains skewness. Skewness is best seen and communicated with the use of histograms and probability distributions.
Left-Skew Vs Right-Skew
Before getting into how skewness is interpreted, it is important to understand the difference between left skew and right skew.
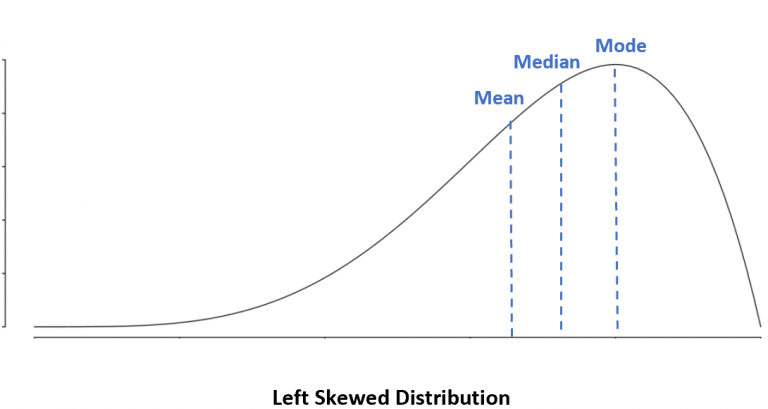
Left-skewness or negative skew refers to a sampling distribution, histogram or probability distribution that has its tail on the left side and the hump on the right. In the left-skewed case, the mean (average) is less than the median and the median value is less than the mode (most common value). Most of the values are on the right where the hump is.
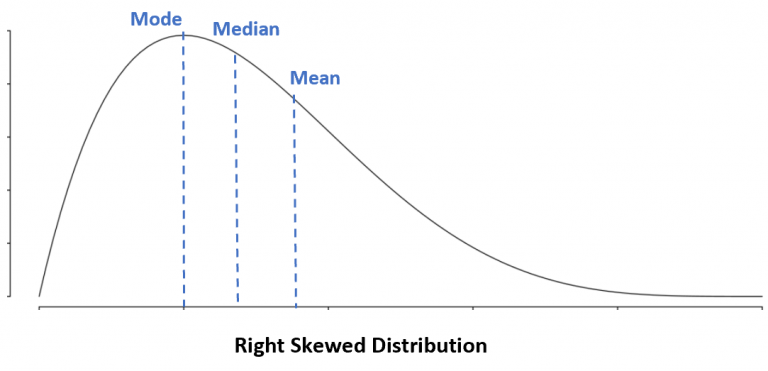
Right-skewness or positive skew occurs when the mode is less than the median value and the median is less than the mean. The tail is on the right side and the hump is on the left side where most of the values are.
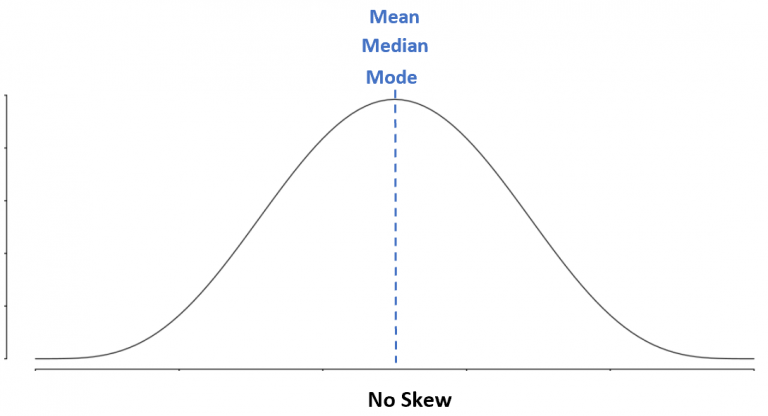
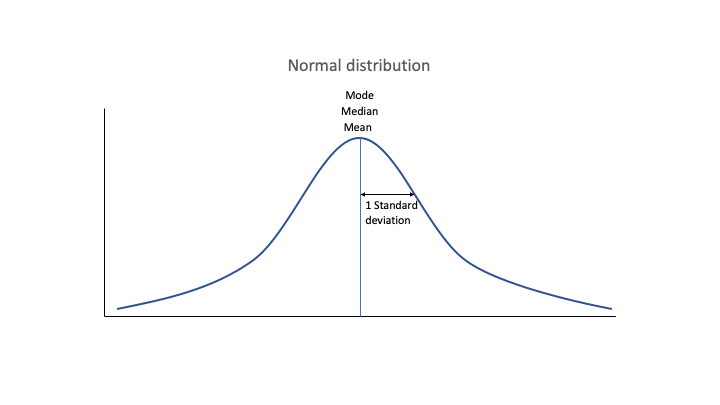
If there is no left skew or right skew then there is zero skewness. The sampling distribution, histogram or probability distribution is symmetric about the mean. The values for the mean, median and mode are all equal to each other.
Pictures from https://www.statology.org/left-skewed-vs-right-skewed/.
Calculating Skewness
This section is about calculating skewness. In a statistics course, you may be asked to compute skewness with paper and pencil to have an idea of what is going on behind the scenes. It is way more practical and faster to use software compute skewness.
Given the data values of 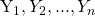 , the formula for skewness is:
, the formula for skewness is:
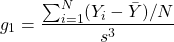
Note that 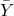 is the mean of the Y-values, N is the number of data points and
is the mean of the Y-values, N is the number of data points and 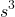 is the sample standard deviation to the power of 3. The above formula is the Fisher-Pearson coefficient for skewness.
is the sample standard deviation to the power of 3. The above formula is the Fisher-Pearson coefficient for skewness.
What is used in many software programs is the adjusted Fisher-Pearson coefficient for sample skewness.
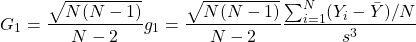
Reference: https://www.itl.nist.gov/div898/handbook/eda/section3/eda35b.htm
The Normal Distribution Is Symmetric
The normal or Gaussian probability distribution is quite famous. It has a nice symmetric bell-shape curve with neat statistical, probabilistic and mathematical properties. As the normal distribution is symmetric, the mean, median and the mode of a normally distributed random variable is the same. As the median is equal to the mean, half of the values are above the mean and the other half of values are below the mean.
Exponential Distribution & Skewness
The Normal distribution is well known for many as it is taught in introductory probability and statistics courses. Do keep in mind that not every histogram nor sampling distributing will be symmetric. This is why skewness exists.
With an exponential distribution many of the lower values are common and the higher values are less common. This is associated with a right (positive) skew in the values as shown in a sample histogram below.
A continuous random variable that has an exponential distribution has the following probability distribution.
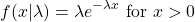
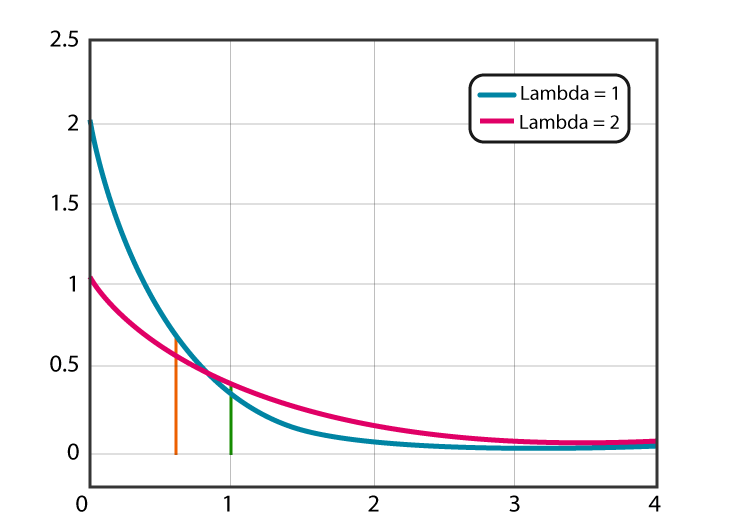
The exponential distribution is right skewed regardless of the choice of the lambda (λ) parameter.
Using Software/Programming To Compute Skewness
Excel
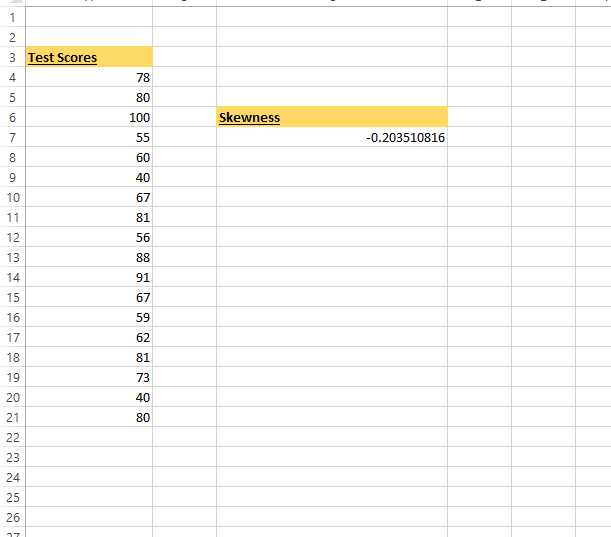
Although Excel is not a programming language, it does have a lot of utility while being fairly user friendly. The key command for computing skewness is =SKEW(). Inside the brackets for the skewness function, do input the cell or range of cells that include numeric values.
In the screenshot I use the command =SKEW(A4:A21).
R Statistical Software
The statistical software R can be used to compute skewness for a given list of values. You do need to install the e1071 package in R to be able to access the skewness() function.
install.packages("e1071")
library(e1071)
test_scores <- c(78, 80, 100, 55, 60, 40, 67, 81, 56, 88, 91, 67, 59, 62, 81, 73, 40, 80)
# Gives -0.1708486, different than Excel's -0.203510816
skewness(test_scores)
With the same test score values, R's skewness function gives a slightly different measure. It could be that a different skewness formula is used.
Python
With Python, you can use the skew function from scipy.stats.
from scipy.stats import skew
test_scores = [78, 80, 100, 55, 60, 40, 67, 81, 56, 88, 91, 67, 59, 62, 81, 73, 40, 80]
# Python gives -0.186143
print(skew(test_scores))
Resources On Skewness
You can find a lot of information on the concept of skew. Skewness applied to the normal distribution, financial returns and to sampling distributions that are not normally distributed.
- https://www.investopedia.com/terms/s/skewness.asp
- https://corporatefinanceinstitute.com/resources/knowledge/other/skewness/
- https://brownmath.com/stat/shape.htm
- https://www.spcforexcel.com/knowledge/basic-statistics/are-skewness-and-kurtosis-useful-statistics
- https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.skew.html
- http://www.r-tutor.com/elementary-statistics/numerical-measures/skewness

Posted with STEMGeeks
HTTP is in use instead of HTTPS and no protocol redirection is in place. Be careful and do not enter sensitive information in that website as your data won't be encrypted.
It's also a good habit to always hover links before clicking them in order to see the actual link in the bottom-left corner of your browser.
This auto-reply is throttled 1/20 to reduce spam but if it still bothers you reply "OFF HTTP". Or reply REVIEW for manual review and whitelisting.