Solving Proportions - A Guide
Hi there. In this math guide, I cover the topic of solve proportions. The goal is to solve for the unknown variable while two fractions are equal to each other. I start with the basic cases and build up into tougher cases.
Screenshot images are from Windows Snipping tool with witeboard.com & my Wacom Tablet.

Topics
- Reasoning In Groups
- Examples Of Solving Proportions
- Extension - Using Distributive Law
Reasoning In Groups
To explain the concept of reasoning in groups I start with an example. If 5 apples cost $2 then how much would 10 apples cost? Ten apples is two groups of five apples. One group of five apples costs $2 so two groups of 5 apples would cost six dollars.
Here is another example. Three pair of socks are for $10. How many pair of socks can you buy for $40? As every $10 buys 3 socks, $40 would be 4 times $10. This is 4 groups of $10 which is also 4 groups of 3 socks. Fourty dollars would buy 12 pair of socks.
The representation of the above two examples in fractions form would be the following.
Example One - Five Apples Cost $2
Example Two - Three Pairs Of Socks Cost $10
Examples Of Solving Proportions
The examples here are shown with screenshots. Cross multiplication is shown with the use of arrows.
Example One
Two out of eight is equal to what number out of 100?
Set up the two fractions with two eighths on the left side and x out of 100 on the right side. Cross multiplication is indicated with the green arrows. For the left side it is two multiplied by one hundred to obtain 200. The right side would be eight times x. A linear equation is formed as 200 = 8x. Eight times something is equal to two hundred. The value of x here is 25.
Example Two
Five ninths is equal to 7 out of x. Solve for the value of x.
Example Three
Three sevenths is equal to x out of 100. Solve for the value of x.
Extension - Using Distributive Law
There are a few cases where the algebra topic of the distributive law is applied when it comes to solving proportions & cross multiplication. Let's look at a few examples.
Example One
Solve for x in 2/(x + 2) = 7/4.
As you have two fractions equal to each other you can do cross multiplication. The left side would be eight. The right side would be the product of 7 and (x + 2). With the right side you have a number multiplied by a binomial expression. In this case the distributive law would applied to obtain 7x + 14. Solve the linear equation to obtain the answer of x = -6/7.
Example Two
In 1/7 = (2x - 5)/3 solve for x.
Posted with STEMGeeks
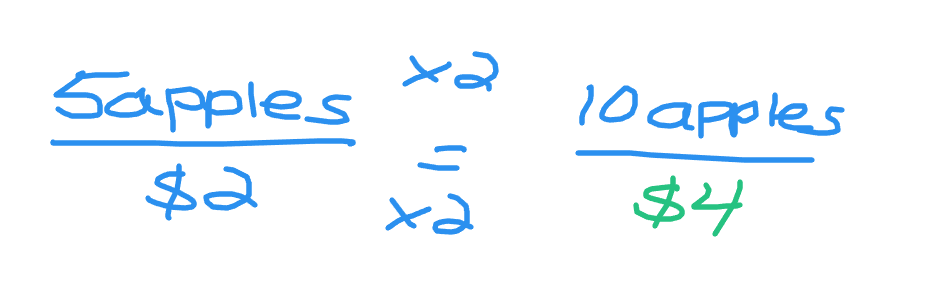
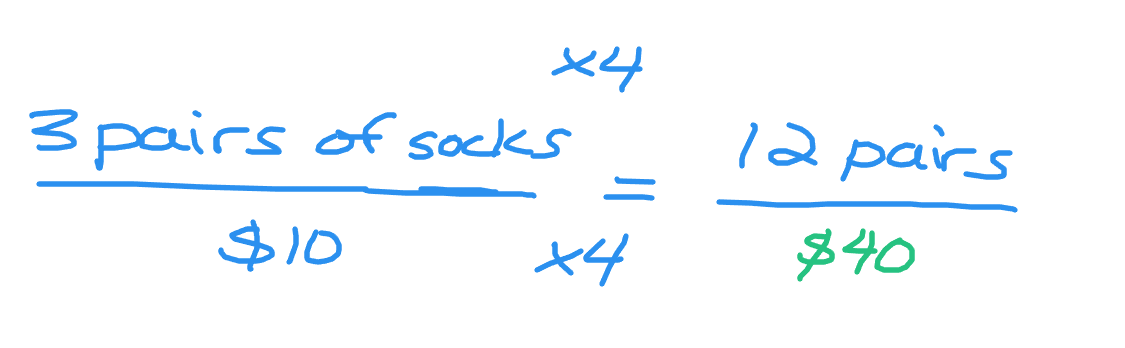
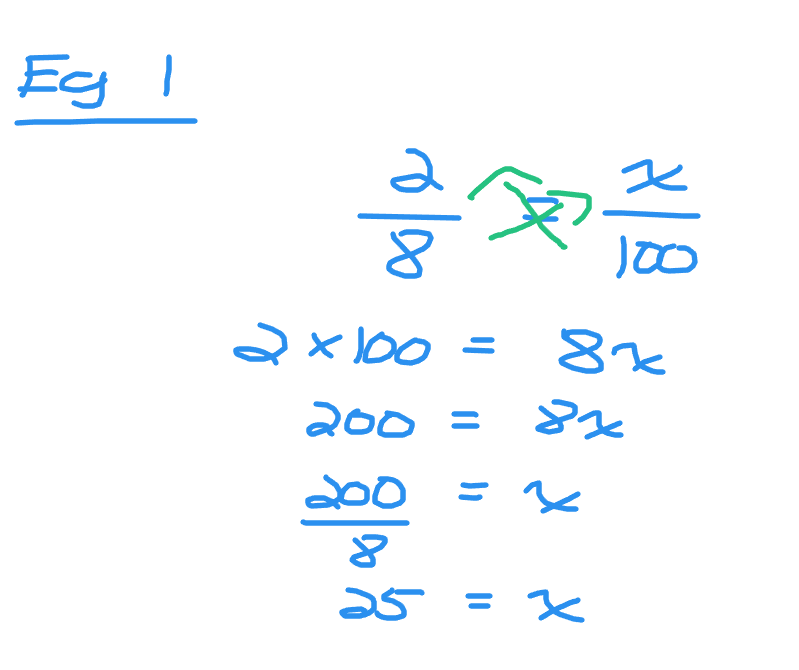
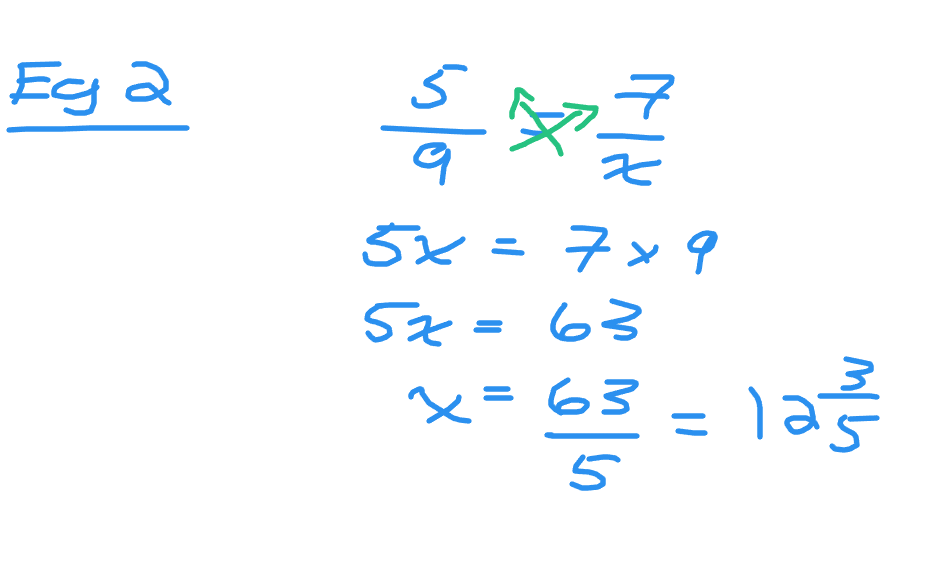
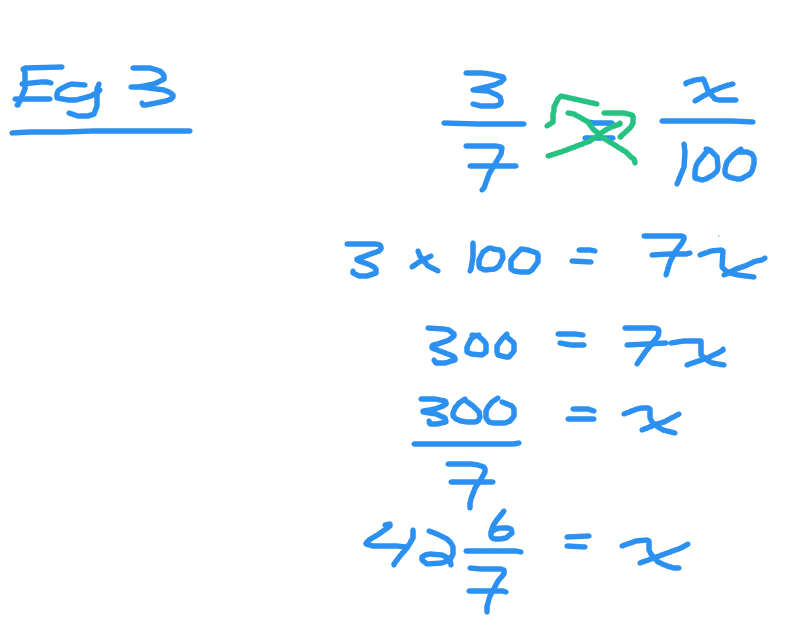
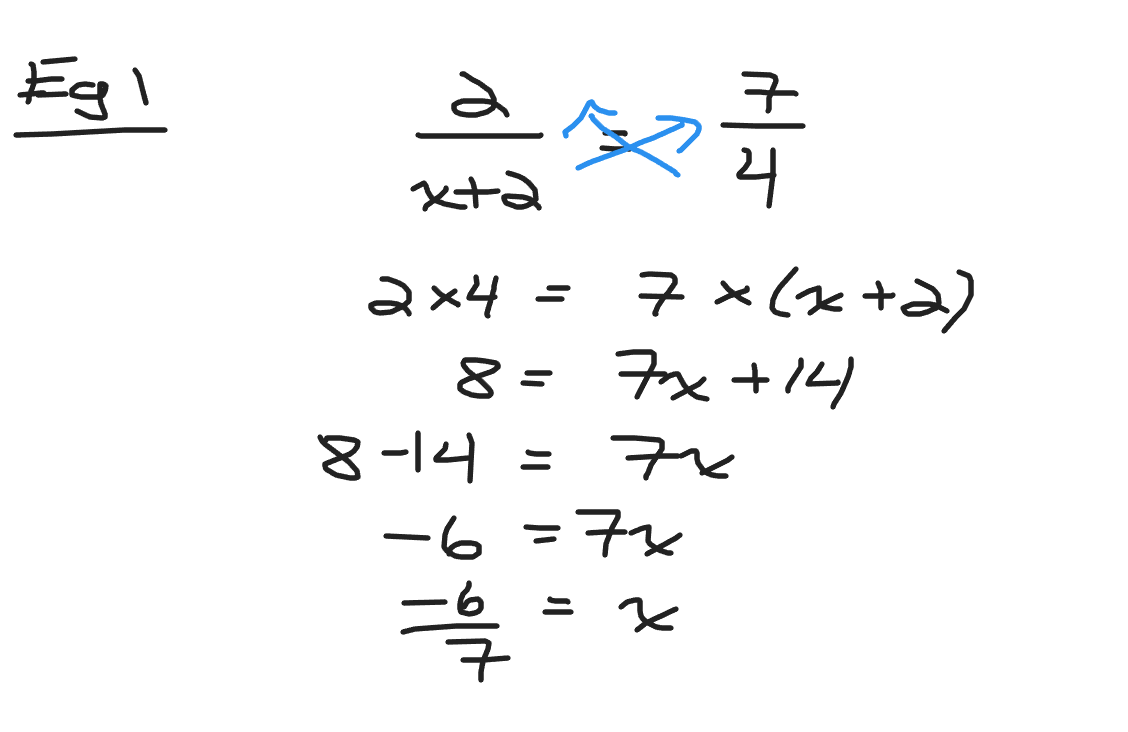
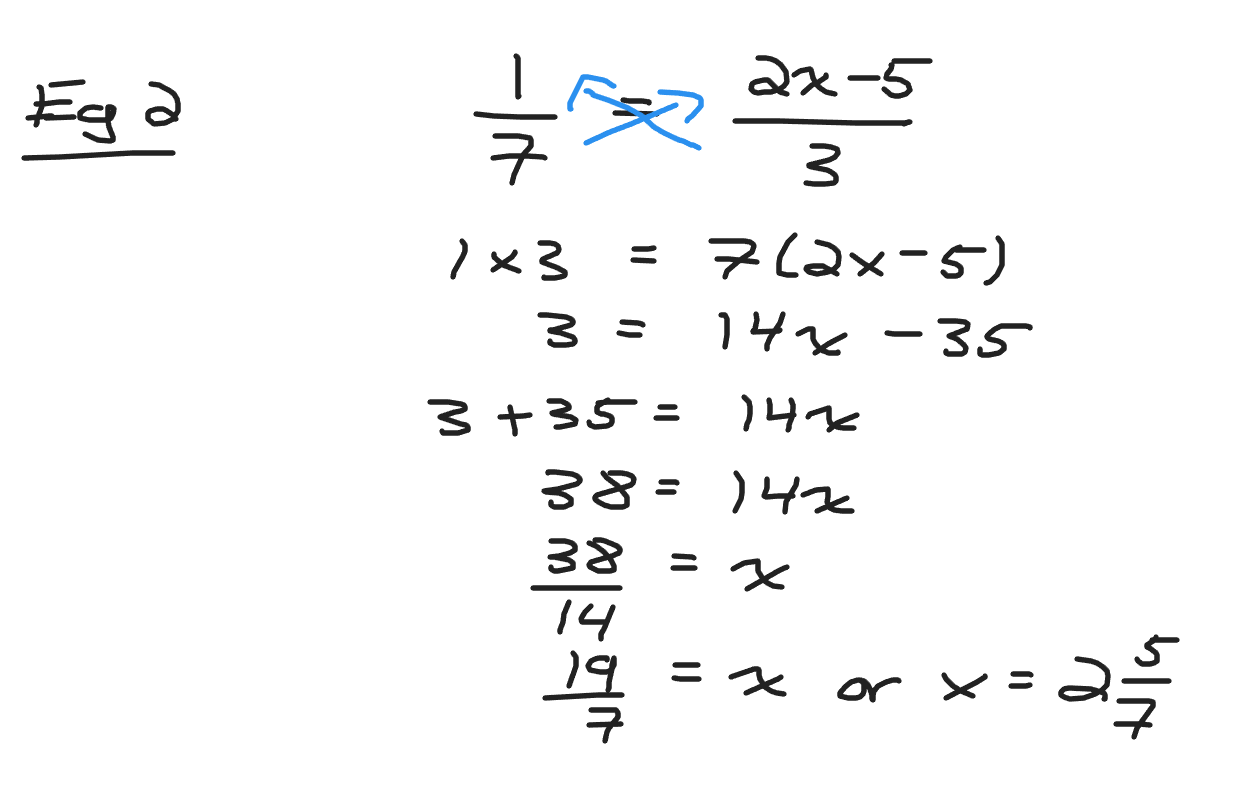
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
thanks for explaining it
!1UP
You have received a 1UP from @gwajnberg!
@stem-curator
And they will bring !PIZZA 🍕.
Learn more about our delegation service to earn daily rewards. Join the Cartel on Discord.
I gifted $PIZZA slices here:
@curation-cartel(10/20) tipped @dkmathstats (x1)
Join us in Discord!