Solving Math Inequalities With Quadratic Equations
Hi there. In this math post, I cover the topic of solving math inequalities with quadratic equations. This topic is algebraic in nature. It is assumed that the reader is comfortable with quadratic equations, the algebra topic of factoring, inequality signs (<, >, ≤, ≥) and working with inequalities.
Math text done with LaTeX rendering through Quicklatex.com.

Topics
- Solving Quadratic Inequalities With Factoring Techniques
- Quadratic Inequalities & The Quadratic Formula
Solving Quadratic Inequalities With Factoring Techniques
Example One
Solve for x in 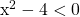 .
.
The objective is to find x-values such that the quadratic function  is less than 0. First, we factor the quadratic to obtain the x-intercepts for the quadratic.
is less than 0. First, we factor the quadratic to obtain the x-intercepts for the quadratic.
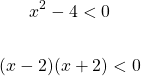
The x-intercepts for the quadratic function are -2 and 2. These x-intercept values make the quadratic function zero. Use the values of -2 and 2 to help find valid values for x that make the inequality true with the use of a table.
| x | y |
|---|---|
| -2 | 0 |
| -1 | -3 |
| 0 | -4 |
| 1 | -3 |
| 2 | 0 |
I use a number line type of diagram to determine intervals where the quadratic is positive or negative. I use the test values of -3, 0 and + 3 for determining the sign of the quadratic function.
If a graphing tool is allowed you can use Desmos to visualize the solution set.
The quadratic function for this question is negative when x is greater than -2 or when x is less than 2. In math notation this is 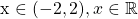
Example Two
Solve for x in 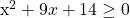 .
.
The two factors of 14 that add up together to 9 are 7 and 2. Factoring the left side of the inequality yields:
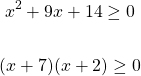
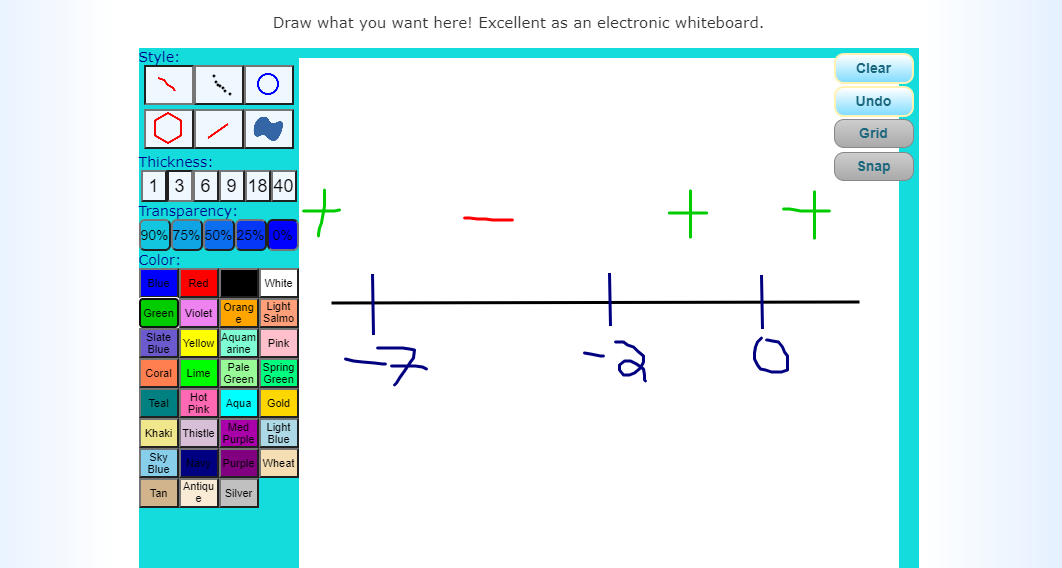
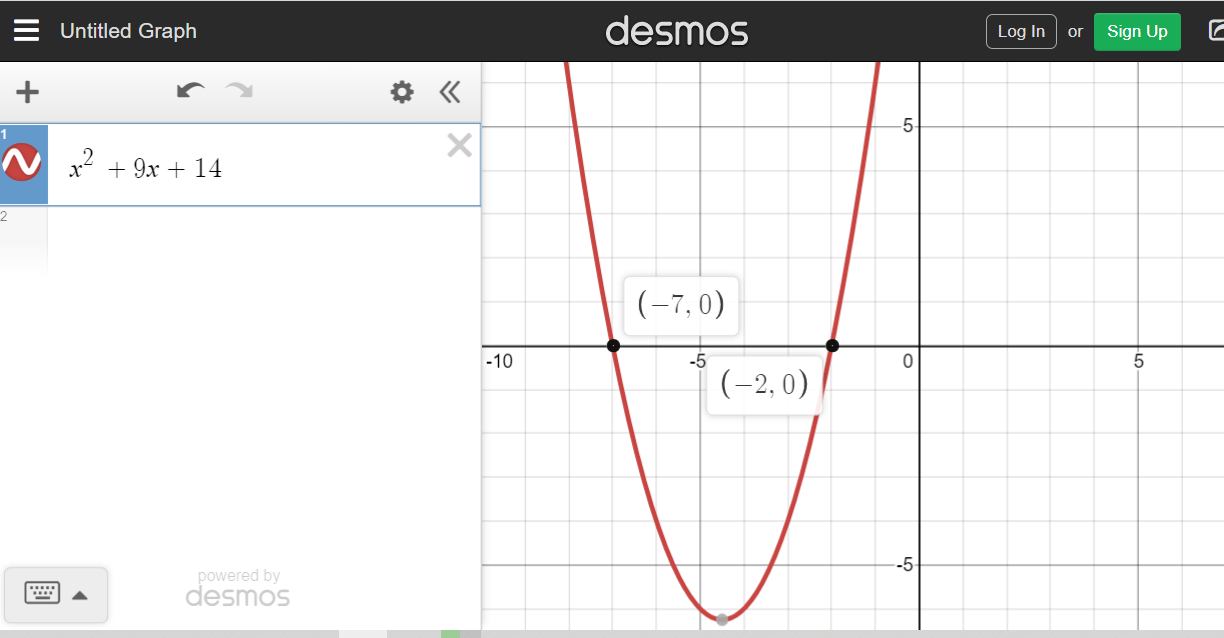
From the left side, the x-intercepts are -7 and -2. Create a table with the values of -7 and -2 as key values.
The solution set is when x is less than or equal to -7 or when x is greater than or equal to -2.
Example Three
Solve for x in  .
.
Start with adding both sides by 2. Afterwards factor a negative one as a common factor.
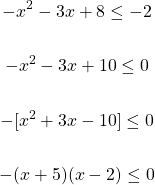
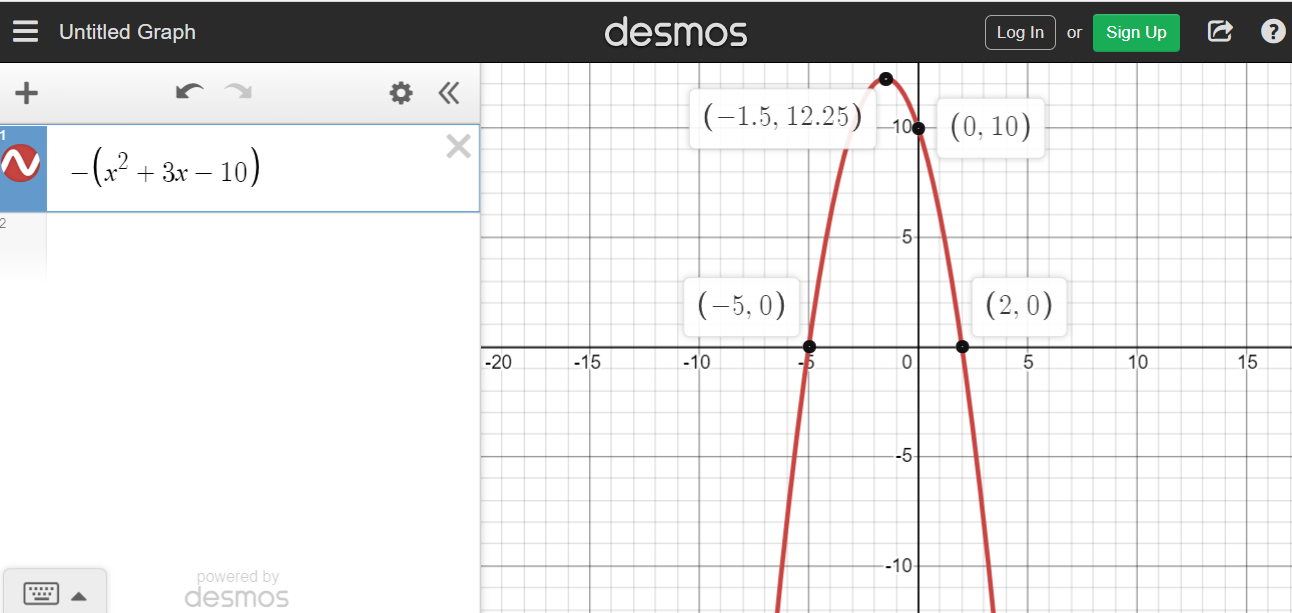
The x-intercepts for the quadratic on the left side are -5 and +2. A table can be created to help identify the intervals where the quadratic is negative or positive. Be careful of the negative sign. The negative sign would change the signs.
The solution set for x in  is when
is when x is less than or equal to -5 or when x is greater than or equal to 2. In math notation this is 
Quadratic Inequalities & The Quadratic Formula
Not every quadratic can be factored. With non-factorable quadratics, the quadratic formula is needed. As a reference here is the quadratic formula given 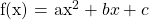 .
.
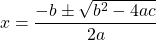
Example
Solve for x in  .
.
fix this
Using the quadratic formula for  gives:
gives:
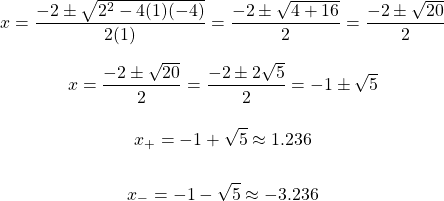
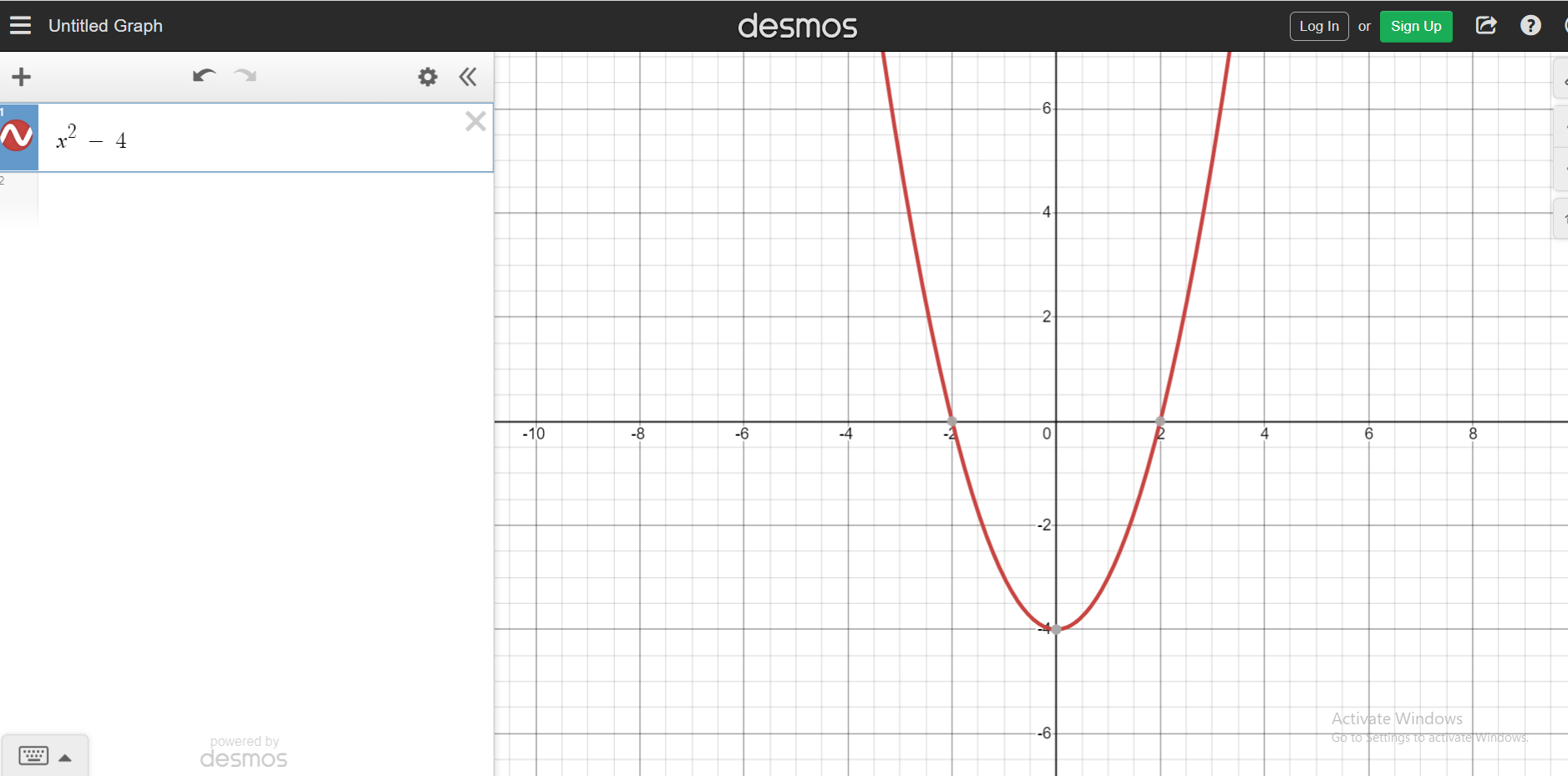
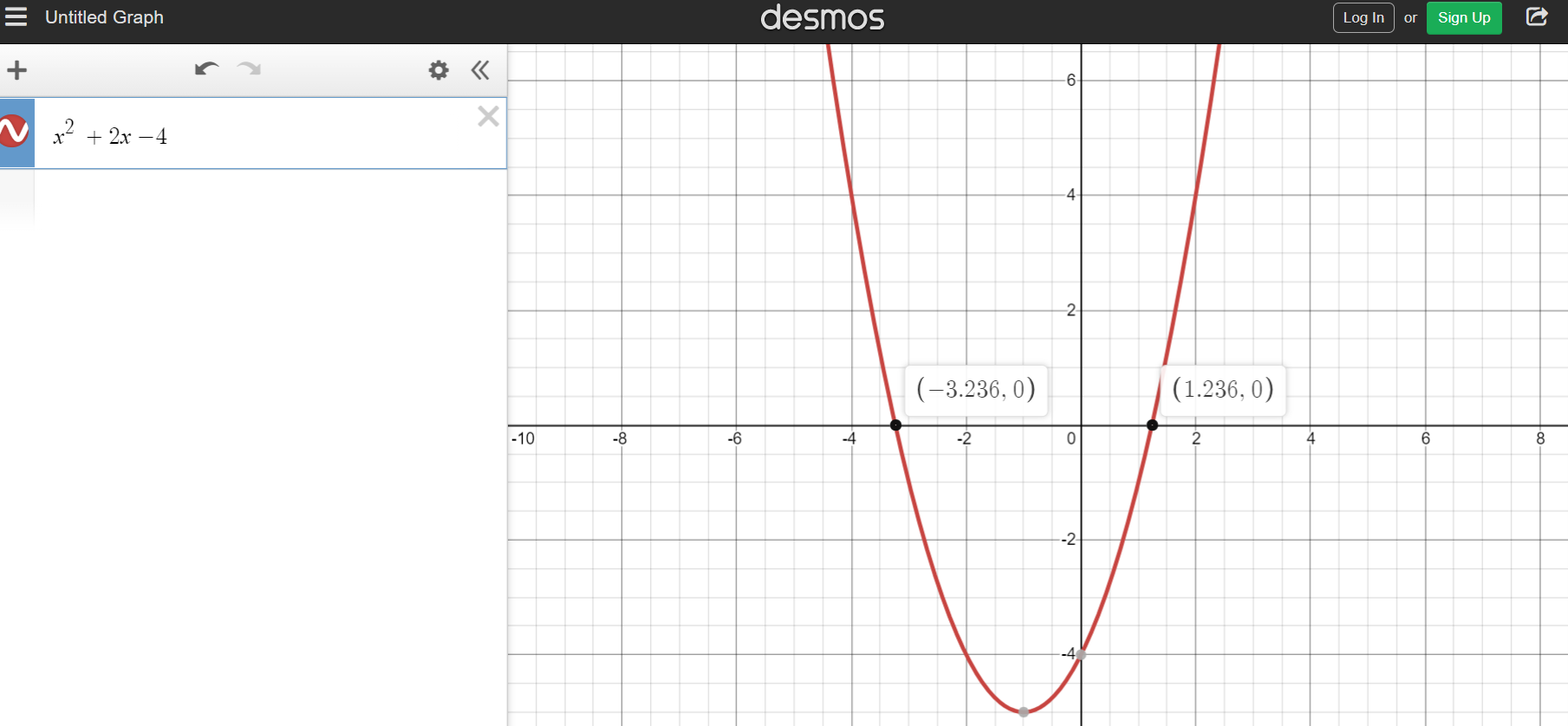
I have decided not to show a table here but have included a Desmos screenshot.
The quadratic  is less than 0 when
is less than 0 when 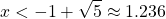 or
or 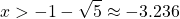 .
.

Posted with STEMGeeks


Congratulations @dkmathstats! You received a personal badge!
Wait until the end of Power Up Day to find out the size of your Power-Bee.
May the Hive Power be with you!
You can view your badges on your board and compare yourself to others in the Ranking
Check out the last post from @hivebuzz: