Solving Linear Inequalities
Hi there. In this math post, I go over finding solutions when it comes to dealing with linear inequalities. Learning linear inequalities just gives an extra tool for the algebra toolbox. There are no real applications for this.

Topics
- Dealing With No Equal Signs
- Watch Out For Negatives
- Practice Problems
- Solutions to Practice Problems
Dealing With No Equal Signs
A lot of algebra solving problems involve solving for x when there is an equal sign. However, when the equal sign is replaced with these signs ≤, ≥, <, >, things are slightly different. Different as in when it comes to solving, stating the solutions, graphing and dealing with those pesky negative signs.
The focus in this post is on the algebra for solving linear equations. Graphing linear equations is another topic and solving polynomial inequalities is another topic as well.
Example One
When it comes to solving for x in x - 3 = 7 the answer of 10 can be found by adding both sides by 3 or by pure intuition. For something like x - 3 > 7, we still add both sides by 3 and obtain the answer of x > 10. With x - 3 < 7, we have the answer of x < 10.
Example Two
Solve for x in 3x + 1 > 10.
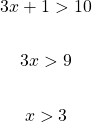
The final line above has the answer expressed as in inequality. You can use more math notation and express the inequality in interval notation as 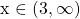 .
.
Example Three
Solve for x in  .
.
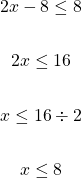
In interval notation, the answer can be expressed as 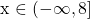 . The square bracket is used after the 8 to indicate that
. The square bracket is used after the 8 to indicate that x can be equal to 8 as well.
Watch Out For Negatives
Negative numbers can be annoying at times. There are times when answers are wrong because of forgetting to multiply by negative one or adding negative numbers incorrectly. Be careful.
Example One
If you have -x > 7 you multiply both sides by negative one. In addition you have to reverse the inequality. After multiplying negative one on both sides in -x > 7 you obtain x < -7.
Example Two
Solve for x in 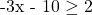 .
.
Practice Problems
Solve for x for the following inequalities.
x - 5 > 1-x < 7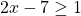
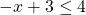
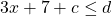
Solutions To Practice Problems
x > 6x > -7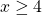

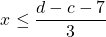

Posted with STEMGeeks