Solving Exponential Equations
Hi there. In this mathematics post, I cover solving exponential equations. This post will cover various cases through examples (without logarithms).

Topics
- Exponential Equations & Exponent Laws Basics Review
- Examples Of Solving Exponential Equations
- Practice Problems With Solutions
Exponential Equations
An exponential equation is an equation that contains an unknown value that is an exponent. Algebra and exponent laws are used as math tools to solve such exponential equations.
Do be careful with a variable to an exponent such as 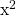 and a number base to an unknown exponent such as
and a number base to an unknown exponent such as 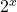 . This post will cover solving unknown exponents.
. This post will cover solving unknown exponents.
Exponent Laws Basics Review
Given a common base a and different exponents we have:
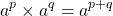
Given a base a and negative exponent we have the reciprocal. Keep in mind there is no negative sign in this.

For the power to a power case, take the product of the exponents.
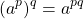
Examples Of Solving Exponential Equations
Example One
In 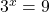 , the value of
, the value of x would be 2. Three squared is equal to 9.
Example Two
Solve for x in 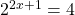 . Rewrite the 4 from the right side as two-squared. Once the number bases are the same on both sides, compare the exponents and solve for
. Rewrite the 4 from the right side as two-squared. Once the number bases are the same on both sides, compare the exponents and solve for x.
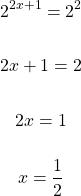
Example Three
Solve for x in the equation 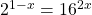 .
.
Rewrite the 16 as 2 to the power of 4.

Apply the power to a power exponent law on the right side. The new exponent with the number base of 2 would be the product of 4 and 2x which is 8x.

As the number bases are the same, the variable x can be solved in the exponents.

Example Four
Solve for x in the equation  .
.
Rewrite the number 49 as 7 squared on the denominator of the right side fraction.
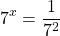
The fraction on the right side can be rewritten as a number base to a negative exponent. This would be 7 to the power of negative 2. Comparing the exponents would give an answer of negative 2 for x.
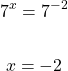
Example Five
Solve for the value of x in 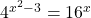 .
.
Rewrite the 16 on the right side as four to the power of two with the exponent x on the outside.
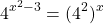
Multiply the 2 and the x on the right side in the exponent.

As the bases are the same at 4, equate the exponents to each other and solve for x.
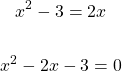
This quadratic can be factored. Two numbers that multiply to negative 3 and add to negative 2 are -3 and 1.

The solutions here are 3 and -1.
Example Six
What is the value of x in 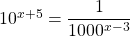
Rewrite the number 1000 as 10 to the power of 3.
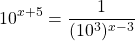
The right side is a fraction that can be written as a base with a negative exponent.
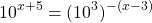
Apply the power of a power exponent law on the right side. The distributive law is applied as well.
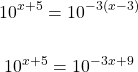
There is now a common base of 10. The exponents from both sides can be equated to each other. After equating both sides to each other, the value of x can be solved for.
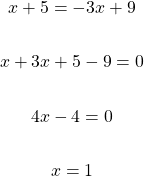
Practice Problems With Solutions
For the following exponential equations, solve for the value of x.
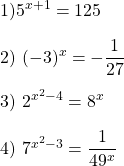
Solutions
x = 2x = -3x = -1 or x = 4x = 1, x = -3

Posted with STEMGeeks
Hi, great post, very simply laid out and for once, I can actually solve these equations but my question is this, please could you give us some practical real-life use cases for the equations? Theory is great, that's for passion exams but practical and situational usage examples would be brilliant!
Thanks in advance and best wishes :-)
Hi. The contents in this post does not involve the use of a calculator nor logarithms.
Examples of solving exponential equations include population growth, exponential decay and compound interest from finance. One Website Example This could be a future post topic amongst many I have planned.
I do agree with applications being supplemented with theory. I just forgot the practical examples here as I wanted to cover the basic cases in solving exponential equations.