Solving Equations That Have Square Roots
Hello there and Happy New Year.
In this mathematics post, I cover solving equations that have square roots in them through examples. An equation that contains square roots are called radical equations.
A lot of these equations are just a variation of solving quadratic equations. Just remember that whatever is inside the square root is greater than zero. No negative values are allowed inside the square root unless you are dealing with complex numbers. It is assumed that the reader is able to do algebra involving quadratic equations, factoring and the quadratic formula.
Example One
Solve for x in the following equation.
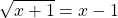
In this case there is a single square root. This square root part is already isolated so we can take the square of both sides. After taking the square of both sides expand the right side and solve the quadratic equation.
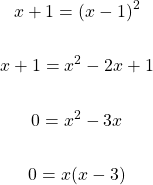
The solutions for x are 0 and 3. Three and zero are valid solutions considering the square root of x + 1.
Example Two - Square Roots On Both Sides
This second example features square roots on both sides. Solving for x here involves squaring both sides.
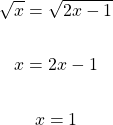
To be sure it is a good idea to check this value of one to see if it makes sense. On the left side we would have the square root of 1 which is 1. The right side would have 2 minus one in the square root which would equal to one. The answer of x = 1 is valid.
Example Three
Solve for x in 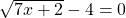 .
.
Move the four to the right side and square both sides to start off. Afterwards, the linear equation can be solved.

The solution here is x = 2 which is valid. Substituting the value of 2 for x in the square root gives the square root of 16.
Example Four - Harder Case
This example does feature a bit of algebra. Solve for x in  .
.
The first step is to isolate for one of the square roots and square both sides.
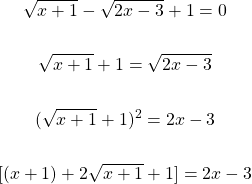
After squaring both sides, combine like terms and isolate the square root part.
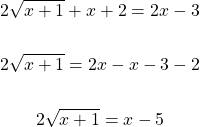
Take the square of both sides again.
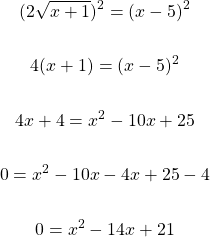
This quadratic equation cannot be factored. The quadratic formula is used to solve for x.
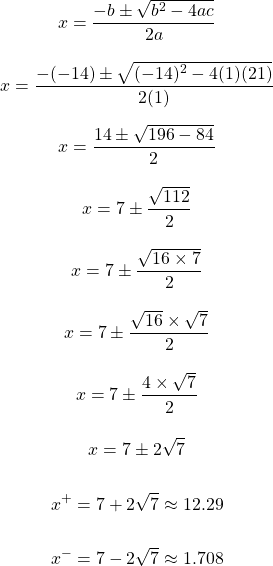
Both these answers have to be checked to see if the equality holds.
Checking the answer of x = 1.708.
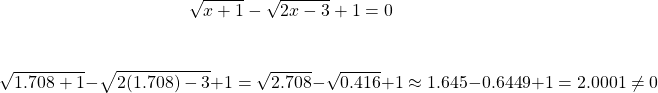
The answer of x = 1.708 does not work. Let's check the approximate valued answer of x = 12.29. (Using the exact value would take a whole ton of work.)
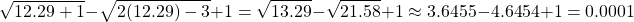
The answer of 7 + 2sqrt(7) or 12.29 works.
Reference: https://www.mathsisfun.com/algebra/radical-equations-solving.html
Posted with STEMGeeks