Simplifying Square Roots
Hi there. In this math guide post, I cover the topic of simplifying square roots. Although this topic does not really have direct applications to real life, this topic is just a part of the algebra toolbox.
Screenshot images are from witeboard.com with the use of my Wacom tablet & stylus pen.

Topics
- Review Of Square Roots
- Simplify Square Roots
- Examples
- Extension - Adding Terms With Square Roots
Review Of Square Roots
The square of a number is when a whole number (integer) is multiplied by itself. One example of a square is 9 which is from 3 multiplied by 3 to equal 9. There is also negative three times negative three to get 9. For this post, I deal with positive whole numbers. Another square would be 25 which is 5 times 5.
Another way to think of a square number is the area of the square. If the side length of a square is seven the area of the square is 49 from seven times seven. Screenshot picture below.
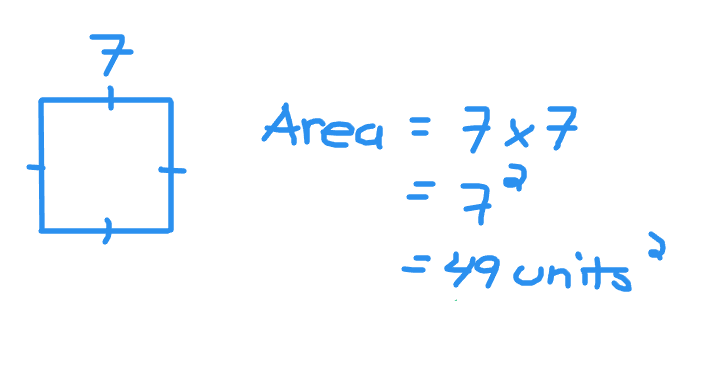
With the square root think of it as what number times itself gets that number. The square root of 100 is 10 as ten times ten is equal to 100. The square root of 64 is 8 as eight times eight is 64.
I feature a table of the positive whole numbers and their squares.
| Whole Number | Square |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
| 11 | 121 |
| 12 | 144 |
Simplify Square Roots
The table above shows the whole numbers and their squares. Going from right to left on the table gives the square roots. What if you wanted to take a square root of a number that is not a perfect square? There is a way to simplify square roots as long as conditions apply.
Given two positive whole numbers a and b the square root of ab is the square root of a times the square root of b. Picture below.

The general strategy when applying this idea is to split the number ab into a and b where one of the two numbers is a perfect square. This will more sense in the examples in the next section.
Examples
Example One
Reduce the square root of 50.
To start think of two numbers that multiply to 50 where at least one of the two numbers is a perfect square. It would be 2 times 25 = 50. Twenty-five happens to be a perfect square as the square root fo 25 is 5.
The square root of 50 would be also equal to the square root of 25 times the square root of 2. Five would be from the square root of 25 and the square root of 2 is left alone. You cannot simplify further from the square root of 2.

Example Two
Reduce the square root of 300.
Three hundred is the product of 100 and 3. Split the square root of 300 into the square root of 100 times the square root of 3. The square root of 100 is known which is 10 and the square root of 3 is left alone.

Example Three
What is the simplified version of the square root of 40?
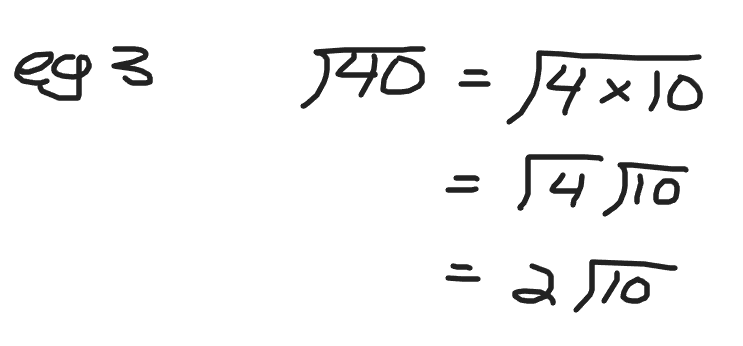
Extension - Adding Terms With Square Roots
This section is more for upper year high school students and first year university students. There are times when you need to reduce fractions that contain square roots. People generally prefer smaller and simpler numbers for final answers.
Example One
Simplify sqrt(200) minus 3sqrt(2).
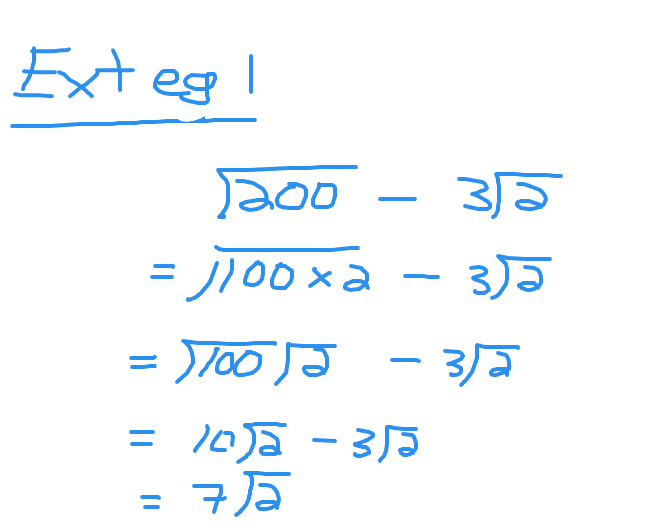
Example Two
Simplify sqrt(250) + 2 + 3sqrt(10).

Posted with STEMGeeks
Haha, I remember this is the topic that started tripping people out back in school.
!discovery 37
This post was shared and voted inside the discord by the curators team of discovery-it
Join our community! hive-193212
Discovery-it is also a Witness, vote for us here
Delegate to us for passive income. Check our 80% fee-back Program
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.