Simple Math Proofs With Even & Odd Numbers
Hi there. In this math post, I cover simple math proofs that involve even and odd numbers. I do not really do much proofs nowadays and it is not my main specialty but I do know some things here and there.
Although I do say simple math proofs, this topic is more upper high school math schools and first year university math students.
Math rendering done with LaTeX and Quicklatex.com.
Technical Definition of Even & Odd Numbers
An even number is a whole number in which you can make pairs with no one left out. The no one left out refers to a remainder of zero after dividing an even number by 2.
Given an integer (whole number that is positive or negative) k, an even number can be expressed as:
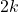
An odd number is a whole number is an even number plus one. There is one left out after making pairs. Some prefer to define an odd number as an even number minus one.
Note that
Given an integer k, an odd number can be expressed as 2k + 1 or 2k - 1.
Addition Case For Even & Odds
When it comes to math proofs, you have to make sure the proof covers for all cases and not for a simple example. Doing a proof that is trying to prove an even number plus an even number is even should not involve an example such as 4 + 4 = 8. What about the 2 + 2 case and the other cases?
Even + Even = Even
To show that two even numbers added together are even, start with defining the two even numbers. The first even number is defined as 2k and the second even number is defined as 2j. Note that the integers k and j could be equal. We have the following:
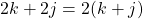
What I did was common factor out a 2. The sum of k and j in the brackets is an integer. Two times any integer or sum of integers is an even number.
You could extend this to more than two even numbers added together. Let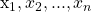 
be integers.
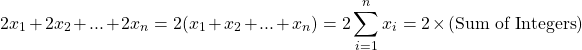
Even + Odd = Odd Case
For this proof, start with defining an even number and an odd number. Let 2k be the even number and let 2j + 1 be the odd number where the integers k and j could be equal. Adding the even number and odd number together gives:
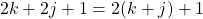
Like in the previous proof, I common factored out the 2 from 2k and 2j. The one is not factored. Adding the integers k and j gives an integer.
The product of 2 and (k + j) is an even number. Adding the one to an even number makes the sum odd.
As a self-exercise, you can show that regardless of how many even numbers there are in a sum, it takes just odd number in the sum to make the entire total odd.
Odd + Odd = Even Case
Dealing with this case is not too bad. Start with two odd numbers where one is of the form 2k + 1 with k as an integer and the second odd number is of the form 2j + 1. Add the two odd numbers together to obtain an even number as follows:
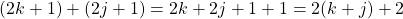
The sum of k and j is an integer. This integer sum is multiplied by 2 making it even. In addition is also two. The sum of two odd numbers is even.
You could also do this where you have two times an integer to obtain the even number.
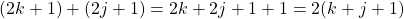
Multiplication Case For Even & Odds
We have dealt with the addition cases so far. Let's look into the multiplication cases with even and odd numbers. Assume that j and k are integers that could be the same.
Even x Even
The product jk is an integer as it is a product of integers j and k. This product is multiplied by two which makes it even. 2jk is multiplied by 2 which makes the product of even numbers even.
Even x Odd
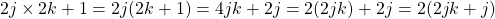
One option is working with 2(2jk + j) which is two times an integer which makes it even. Another option is working with 2(2jk) + 2j which is the sum of two even numbers which is even.
Odd x Odd
With this case, apply the FOIL (First, Outer, Inner, Last) method for multiplying binomials.
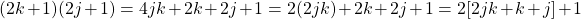
There is some common factoring near the end here. In the end, I wanted to obtain the form of an even number plus one for an odd number. The sum of 2jk + k + j is an integer that is multiplied by two. The plus one at the end makes this and odd number. An odd number multiplied by an odd number is odd.
A Brief Note About Exponent Cases
When it comes to exponent cases with even and odd numbers, you have to look at the base number. If the base number is an even number, you would the even number times even number being even as long as the exponent is a positive integer.
Assuming that the exponent is a positive integer and the base is an odd number, the answer would be odd as there would an odd number multiplied by an odd number.
Posted with STEMGeeks