Proof By Mathematical Induction Examples
Hi there. In this math post, I cover the concept of proof by mathematical induction with a short guide along with examples.
Math proofs are important to show that a math theorem (claim) is true. It is like providing support for an argument.
This math proof technique is not a hard concept but some of the proofs can be difficult to prove. Some math induction proofs involve algebra, problem solving and even understanding of math concepts in the math domain.

Proof By Induction Steps
Let n be a natural whole number. That is n = 1, 2, 3, 4, 5, .... Integer k is another natural number.
Step One (Base Case)
Show that the n = 1 case holds.
Step Two (Induction Hypothesis)
Assume that the n = k case holds.
Step Three
Show that the n = k + 1 case holds. (One step ahead)
This step is the most important one and is not easy to do in some cases. Some proofs that involve proof by induction require heavy algebra or some algebra tricks.

Examples
Example One
Prove that 1 + 2 + 3 + ... + n is equal to n(n+1) / 2 for all n being positive whole numbers (natural numbers).
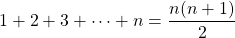
Start with the base case with n = 1. One is equal to 1 x 2 then divided by 2 gives 1. The equality holds for the base case.
With the second step (Induction Hypothesis) assume that for an integer k being whole numbers (k = 1, 2, 3, 4, ...), this holds true.
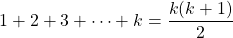
The next & final step is to prove that the equation holds for the k + 1 case. Is the below equation true?
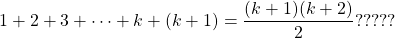
Start with the left side. The sum from 1 to k is associated with the induction hypothesis
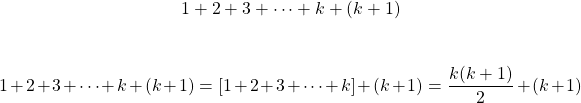
Find a common denominator and common factor out a (k + 1). Once the steps are done the k + 1 case will show to hold true.
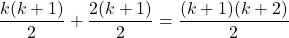
Example Two
Claim: 5 to the power of n then minus 1 is divisible by 4.
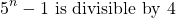
Base Case (n = 1): 5 to the power of 1 is 5 and then subtract 1 gives 4 which is divisible by 4. Check.
For the next step assume the following as the induction hypothesis. (n = k true)
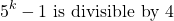
Now the n = k + 1 case has to be proven. Start with 5 to the power of (k + 1) minus 1.
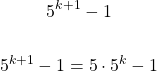
This next step is important. After 5 to the power of k, I subtract 1 and add 1 which is essentially adding by zero. Notice the use of brackets.
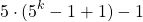
Apply the distributive law only on the plus one. It would be 5 times the plus 1 here.
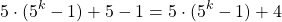
This is a desired form. From the induction hypothesis, 5 to the power of k minus 1 is divisible by four. Five times the quantity of 5^k - 1 is divisible by four as well. The plus 4 is also divisible by 4. This quantity above is all divisible by 4 as the n = k + 1 case is proven which concludes this math induction proof.
Example Three
I feature an inequality in this example. A factorial n! is equal to 1 x 2 x 3 x ... x n for whole numbers n = 1, 2, 3, ....
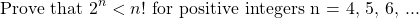
The base case here is not n = 1. It is n = 4 here. Two to the power of 4 is 16 and 4! = 4 x 3 x 2 x 1 = 24. Four factorial is larger than 2 to the power of 4. The base case holds.
For the induction hypothesis, assume that 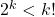 .
.
Now prove the following:
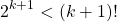
Start with the right side which is the factorial part.
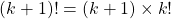
From the induction hypothesis we have k factorial greater than two to the power of k. Apply this induction hypothesis with (k + 1) multiplied on both sides.
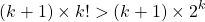
The quantity k + 1 is at least 5 as k is at least 4. This k + 1 part is greater than 2.
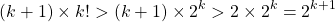
This means that 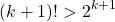 and the induction proof is complete.
and the induction proof is complete.

References
- http://comet.lehman.cuny.edu/sormani/teaching/induction.html
- https://people.uwec.edu/mbirika/M314_Notes/Ch.5_Math_Induction_Examples_Worksheet.pdf
- http://home.cc.umanitoba.ca/~thomas/Courses/InductionExamples-Solutions.pdf
Posted with STEMGeeks
Very well articulated. I've finally grasped the concept of mathematical induction. Thank you for providing this information.