Permutations Without Repetition & Combinations
Hi there. In this mathematics post, I cover the topic of combinations and permutations. These two topics are from the math field of combinatorics and in probability.
Topics
- Permutations Without Repetition
- Combinations For Arranges Without Considering Order
Permutations Without Repetition
For permutations I will start with an example. A selection committee wants to choose between Brian, Harry, Robin, Hugo and Jack for the roles of President, Vice President and Chief Technology Officer (CTO). How many ways can we assign three roles from five candidates?
The committee wants to choose a president first. There are 5 choices for president. It could be either Brian, Harry, Robin, Hugo or Jack. After a president is chosen, there are 4 people left for a Vice-President position. Once the Vice President spot is chosen there are 3 people left for the CTO spot.
The number of ways of selecting 3 out of 5 people into 3 roles is five pick three. In math notation this is denoted as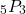 
. The calculations would be 5 x 4 x 3 = 20 x 3 = 60. There are 60 ways to choose three people in 3 different roles from 5 candidates.
Here is a partial table of what the permutations/arrangements looks like.
| Permutation # | President | Vice-President | CTO |
|---|---|---|---|
| 1 | Brian | Harry | Robin |
| 2 | Brian | Harry | Hugo |
| 3 | Brian | Harry | Jack |
| 4 | Brian | Robin | Hugo |
| 5 | Brian | Robin | Jack |
| 6 | Harry | Brian | Robin |
| 7 | Harry | Brian | Hugo |
| 8 | Harry | Brian | Jack |
| 9 | Robin | Brian | Harry |
| and | so on | ... | ... |
Factorials - Quick Definition
A factorial is a compact mathematical expression which represents the product of positive whole numbers. Instead of writing 5 x 4 x 3 x 2 x 1 we just write 5!. Factorials are never negative and it is defined that 0! = 1.
The general formula for a factorials is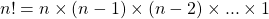 
.
General Formula For Permutations
The example above dealt with selecting 3 people from 5 candidates which gave 60 ways. The calculation was 5 x 4 x 3 = 60. In math notation for permutations this is:
If we want to know how many ways we can choose k items/people from n options where order matters, we have the general formula for permutations.
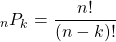
Example Two
Tom is voting for his favourite music artists at the end of the year. Tom votes for his 3 favourite music artists out of 78 choices. In this vote, a number one vote has 3 points, a number two has 2 points and a number three vote has 1 point. A list of the most popular music artists is published near the end of the year with the most popular artist having the most points.
How many ways can Tom have in his top 3 vote?
There are 78 choices to pick from and Tom can only pick 3. This is 78 pick 3.
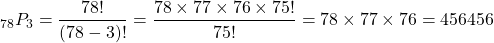
You can use a calculator to compute 78 pick 3 to get 456456.
Example Three
What if Tom had less choices to choose from? Tom reduces his list from 78 choices to 20 artists to choose from for his top 3 vote. How many ways can Tom pick 3 from 20 music artists?
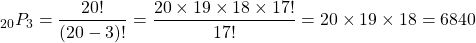
In this case, picking 3 from 20 music artists yields 6840 ways. This is way less than picking 3 from 78 music artists which was 456456 ways.
Combinations For Arrangements Without Considering Order
With permutations, order does matter. When it comes to combinations order does not matter. In the first example, 3 people from 5 candidates are chosen for three different positions. If this was a combination we would have 3 people from 5 candidates being chosen for a business trip (as an example).
The general formula for determining the number of combinations is:
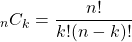
Example One Revisited But With Combinations
Let's revisit the selection committee example. The selection committee wants to choose between Brian, Harry, Robin, Hugo and Jack for 3 big roles in a company. How many ways can we choose 3 people from the five candidates?
With permutations it did matter if a candidate was chosen and for which role he is assigned to. Under combinations, being picked first is the same as being picked second or last as all three chosen people land a big role in the company.
For the math calculations it is:
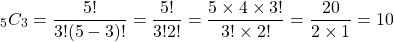
Example Two
Jenny is leaving for a weekend trip to the beach. She has 2 hats to choose from 8 hats in her closet. How many ways can Jenny choose 2 hats?
This one is straight forward as it is 8 choose 2 or 8C2 = 28.
Example Three
A group of 5 men and 7 women want to create a committee of 3 men and 3 women. How many ways can this committee be formed?
From the men it is choosing 3 men from 5. This is 5 choose 3 or 5C3 = 10.
With the women it is choosing 3 women from 7. This is 7 choose 3 or 7C3 = 35.
Multiply the two results to obtain 350 ways to form a committee of 3 men and 3 women from 5 men & 7 women.
Posted with STEMGeeks