Math Word Problems Dealing With Averages
Hi there. In this post, I will cover word problems dealing with averages (mean).

Topics
- A Review Of Averages & The Arithmetic Mean
- Word Problems Dealing With Averages
- Practice Problems
- Solutions to Practice Problems
A Review Of Averages & The Arithmetic Mean
An average refers to a central value for a set of numbers. You could view as a summary type of numbers which contains information from the numbers in its corresponding set.
In everyday speak the average refers to the arithmetic mean. This is where we add up all the numbers together to obtain a total and then divide by how many numbers there are. There are other averages and other values of central tendency out there with its own calculations, meanings and uses.
If you have sample data from a larger population, the average for a sample is represented by the symbol 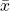 (lowercase xbar).
(lowercase xbar).
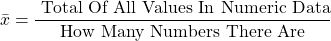
For a more technical and mathematical representation you would have this formula. This is for a sample of values represented as 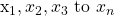 .
.
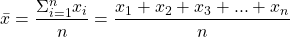
The variable n refers to how many numbers there are in the numeric data set of values. It is also referred to the sample size. A larger sample size or value of n is more informative in the sense that the sample captures a larger portion of the population. Averages from a larger sample size are more closer to the average of the population of interest. (The Law Of Large Numbers concept could be a different post. )
This image is from https://sites.google.com/a/whps.org/mrs-murray-s-math-site/unit-1---intro-to-statistics

Example One
Every Saturday evening, John likes to eat pizza. The number set below represents the number of slices of pizza he eats from ten Saturdays.
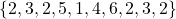
The average amount of pizza slices that John eats involves adding up all the numbers from the ten Saturdays. This total is 30. From this total divide by 10 from the ten Saturdays. John' average amount of pizza slices that he eats on a Saturday is 3.
Example Two - Same Average Score But Different Test Scores
Janine has these Grade 10 math test scores from seven tests.

Janine's average from these test scores is 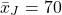 .
.
Tracy who is a classmate of Janine has these math test scores.
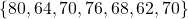
From these test scores Tracy's average is a 70 as well (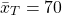 ).
).
Even though their average math test scores are the same, the scores from the tests for Janine and Tracey are different.
If you are given the average only, you do not know the values that are used to compute the average. In addition, the sample size is unknown.
Word Problems Dealing With Averages
This section will deal with word problems involving the average. Averages can be used as one measure of performance or for comparisons. Ideally, it would be better to use additional statistical measures such as range, variance, standard deviation, skewness, etc. for obtaining more information for analysis and comparisons.
Some examples will be shown here.
Example One - Basic Word Problem
Tom is trying to get faster at typing on the keyboard with the TypeRacer website. His words per minute (WPM) in the last eight races are as follows.

What is Tom's average words per minute from these eight races?
To obtain the average words per minute here involves adding up all of Tom's WPM scores from the eight races. The total is then divided by 8.
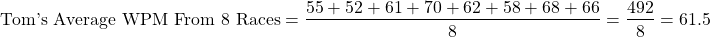
Example Two - Who Did Better?
Tom has a Typeracer rival named Tim. Tim's words per minutes from eight races are as follows.
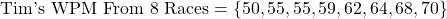
What is Tim's average WPM? Is Tim faster than Tom on average from eight races?
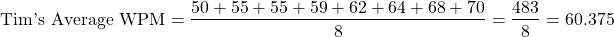
Tim is slightly slower than Tom from the eight Typeracer races.
Example Three - Adding In Another Typeracer Race
Tom adds in another Typeracer Race. In this ninth race, Tom scores 75 WPM. What is Tom's updated average WPM?
From example one, Tom's average WPM from eight races was 61.5 WPM. Recall the calculation that was done to obtain this average.
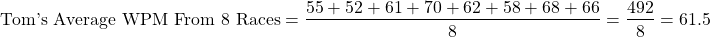
To update the average, add 70 in the numerator and change the denominator from 8 to 9. You would have a new total WPM from nine races divided by 9.

Tom's average WPM increased from 61.5 to 63.
Example Four - What Do I Need To Get A Certain Average?
Marisa has these four math test scores as shown below. She has one more math test to go.
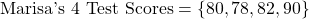
Assume that all of math tests are weighted equally. What math test score would Marisa need if she wanted a 84 average from five math test scores?
Recall that the formula for computing the average takes the total divided by how many numbers there are.
In this case, we have:

The total of 5 test scores would be the product of 84 and 5 which is 420. So far, we have the scores 80, 78, 82 and 90. To find the 5th test score we have determine a number added to the four test scores that equals to 420.
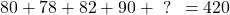
Four hundred twenty minus the four test scores leads to a score of 90. Marisa would need a 90 on the fifth math test to score an average of 84 from the five math tests.
Practice Problems
Question One
The temperatures from city LMN for the last five days are 21, 22, 18, 20 and 25. These temperatures in are in degrees. What is the average temperature from these last five days?
Question Two
The average from four numbers is 70. One of the numbers is twice another number. In addition one of the numbers is ten less than another. What could these four numbers be? (There are other answers too that satisfy these conditions.)
Question Three
With this question we have a table of earnings from Ben and Bob. The earnings covers the last four weeks from their work.
| Ben | Bob | |
|---|---|---|
| Week 1 | 1020 | 900 |
| Week 2 | 1100 | 1000 |
| Week 3 | 970 | 1050 |
| Week 4 | 1200 | 1400 |
Who earned more money on average per week?
Question Four
Robert's scores from nine tests are as follows. All the tests are weighted equally.
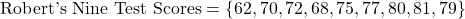
Robert would like a 78 average after the ten tenth test. What test score does Robert need to obtain a 75 average after his ten tests?
Solutions To Practice Problems
An average of 21.2 degrees Celsius from the last five days.
One set of numbers would be 60, 120, 55, 45.
Ben's average earnings per week is $1072.50. Bob's average earnings per week is $1087.50. Bob earns more than Ben on average.
Robert would need a score of 86 to obtain a 75 average after his ten tests.

Posted with STEMGeeks
The average is the one mathematical model that keeps me up at night. Much of the world that we live in is based around this imperfect model, which refuses to adequately incorporate the jagged edges (outliers) of the universe.
The average is actually a statistical measure. It is sometimes used as a estimation measure (guess) for the true average of a larger population.
Yes the average is not perfect but it does capture some/partial information from a sample. The median does a better job dealing with outliers/extreme values. 50% of values are above the median and 50% of values are below the median.
Many people understand averages better than medians, variance, standard deviations, etc. so that is why it is used often.
I think of it as a statistical measure with an underlying mathematical model. It lies at the root of many of our experiments and studies across a large number of fields, as you know. What amazes me is just how well it works, but what astonishes me is that it works at all.
Oh. I think you are referring to sampling distributions.
nicely explained dear.. simple and easy to understand. the way you have broken up the word problem and explained is easy to follow. thanks for sharing. cheers