Math & Finance - Compound Interest & Equivalent Interest Rates
Hi there. In this math & finance post, I talk about equivalent interest rates. This post is very technical and mathematics heavy.
For those not interested in the math details, you can skip to the last section with the Calculator Soup Equivalent Interest Rate Calculator.
Math text rendered in Latex with QuickLaTeX.com

Topics
- Compound Interest Review
- Annual Interest Rates Vs Semi-Annual Vs Monthly
- Extension - Continuous Interest Rates
- Math Examples
- Calculator Soup Equivalent Interest Rate Calculator
Compound Interest Review
Before getting into equivalent interest rates, I would like to cover the concept of compound interest. I use an example to illustrate the concept.
Consider an investment of Bob's $1000 USD into a savings account. The interest rate is 2% annually. Bob is the lender of the $1000 and the financial institution who stores the $1000 is a borrower. Two percent annually means that Bob earns 2% on his $1000 USD while the financial institution pays Bob this 2%.
Bob's investment is $1000 USD plus this 2% of $1000 after the end of the first year. The math turns out to be:
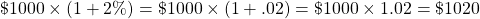
If Bob continues to leave this $1020 into the savings account until the end of the year 2, Bob earns 2% on this $1020 amount. It is 2% on the recent amount. That is the 2% is applied on the original $1000 and the $20 gained as interest. You earn interest on interest.
At the end of year 2, Bob would have $1020 plus 2% of $1020.
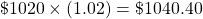
This can also be written as:
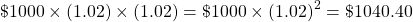
In general, the formula for a future investment with annual compound interest after n years is:
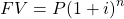
where
- FV is the future value of the principal (P) investment
iis the interest rate for the period (In this case, it is annual interest rate)nis the number of periods

Annual Interest Rates Vs Semi-Annual Vs Monthly
An annual interest rate is an interest rate that is compounded once in a year.
An interest rate that is compounded semi-annually means that there are two compound interest periods in one year. As an example, an interest rate of 10% that is compounded semi-annually would be 5% for each of the two 6 month periods.
With an interest rate compounded monthly, there would be 12 periods in a year. Each compound interest period is one month. If an interest of 12% is compounded monthly, each period would be 1% as in 12% divided by 12.
Example
Consider an interest rate of 12%. Here are the future amounts of a principal of $2000 over 24 months or 2 years.
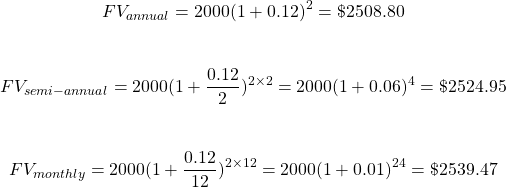
General Formula
A general formula for the future value of a principal under compound interest can be given. We have the principal P, t number of years with n number of periods in a year.
There is also the annual interest rate j_n being compounded n times in one year. Having n = 2 means that the interest rate is being compounded twice or semi-annually. An annual interest rate compounded annually corresponds to n = 1. For a monthly interest rate
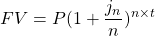
Note that I have not covered the quarterly compounding case. As there are 4 quarters in a year, you would divided the annual interest rate by 4 and multiply the number of years by 4.

Extension - Continuous Interest Rates
This extension is a bit technical and mathematical in nature. You can skip this if you'd like.
What if the interest rate is compounded infinite times? That is the interest rate being compounded all the time.
Compounding the interest rate infinitely many times would result in a continuously compounded interest rate. This would result with using Euler's constant in the form of e ≈ 2.71828. One source on Euler's constant.
The continuously compounded case for the future value of an invested principal would be:

where r is the annual continuously compounded rate and t is the number of years for the investment.
I believe that continuously compounded interest rates are used by actuaries in the insurance industry but don't quote me on this.

Equivalent Interest Rates Math Examples
The concept of equivalent interest rates can be confusing. An interest rate would be quoted at something like 10% which would likely be interpreted as an annual rate. However if there mention of monthly compounding at the 10% rate then the interest rate in the calculations is not actually 10%. The main idea is that 10% annual interest rate is not the same as 10% being compounded monthly.
Annual Interest 10% Vs. Compounded Monthly 10%
Consider two cases. Case one has $1000 invested into a savings account that gives 10% annually. Case two would be $1000 invested into a savings account with a 10% interest rate compounded monthly. Both $1000 investments are invested for 5 years.
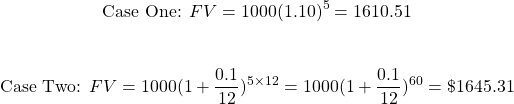
Because of the increased number of compounding periods, case two ends up with a higher future value. Given the same interest rate quoted annually, the future value is highest with the interest rate that is compounded the most frequently.
The order would be Compounded Continuously > Compounded Daily (365 Days a Year) > Compounded Weekly > Compounded Monthly > Compounded Quarterly > Compounded Semi-Annually (Every 6 months) > Compounded Annually
Example One
Given an interest rate of 8% a year, would be the equivalent interest rate if this was compounded monthly?
When it comes to setup there are two sides to the equations. The one side is one dollar compounded at an interest rate of 8% a year. The other side is one dollar compounded at an unknown interest rate that is compounded monthly. You can assume one year. In this case, solve for j12 which is the interest rate being compounded monthly.

Example Two
What is the equivalent interest rate that is compounded semi-annually if the annual interest rate for a savings account is 10%?
Setup the equation and solve for the semi-annual interest rate. You can assume one year here again.
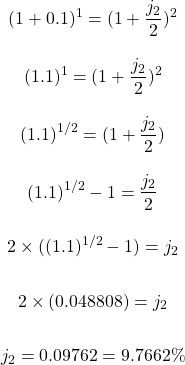
Example Three
A daily interest rate is 2%. What is the equivalent interest rate if this was on an annual basis?
The setup is similar to the ones before. A daily interest rate would be
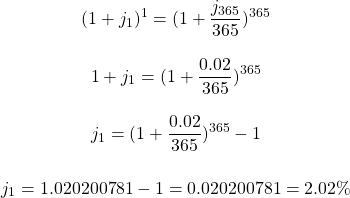

Calculator Soup - Equivalent Interest Rate Calculator
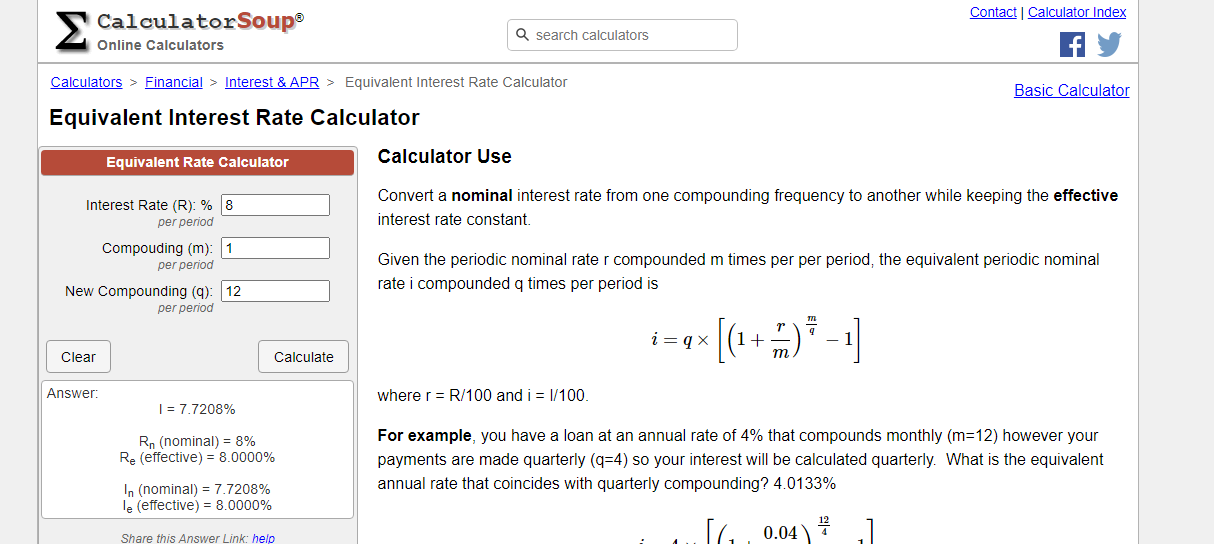
Some of these calculations are technical. With this mind people make online calculators for this. There is an equivalent rates calculator for determining equivalent interest rates based on different compounding types.
Equivalent Rates Calculator: https://www.calculatorsoup.com/calculators/financial/equivalent-interest-rate-calculator.php
Let's revisit example one. The annual interest rate compounded annually is 8%. The corresponding interest rate being compounded monthly is 7.7298%. In Calculator Soup, enter in 8% per period with 1 for the compounding per period. To go from annual interest rate to a monthly interest rate set the new compounding box to 12. There are 12 months for monthly compounding. If you want quarterly compounding set the new compounding to 4 and so on.
Posted with STEMGeeks
https://twitter.com/metodologiaecs/status/1495636498540122113
The rewards earned on this comment will go directly to the person sharing the post on Twitter as long as they are registered with @poshtoken. Sign up at https://hiveposh.com.
well it will help me in understanding where I invest