Logarithmic Functions
Hi there. In this post, I cover the math topic of logarithmic functions. It is assumed that the reader is familiar with exponents , logarithms and logarithm properties.
Math text rendered in LaTeX with Quicklatex.com. I use a few Desmos screenshots too.

Sections
- Review Of Evaluating Logarithms
- The Logarithmic Function
- Log Function As Inverse Of Exponential Function
- Domain & Range Of Logarithmic Functions
- Some Transformations of Logarithmic Functions
- Log Scales
Review Of Evaluating Logarithms
A logarithm is an exponent which solves for x in something like:
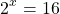
The answer here is x = 4 but can be expressed as 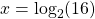 . This is the logarithm of 16 with base 2 is 4. Two to the power of 4 gives 16.
. This is the logarithm of 16 with base 2 is 4. Two to the power of 4 gives 16.
Here is another example.
Solve for x in 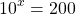 . In other words, ten to what exponent would make this equality true?
. In other words, ten to what exponent would make this equality true?
Take the logarithm with base 10 in both sides to start.

The Logarithmic Function
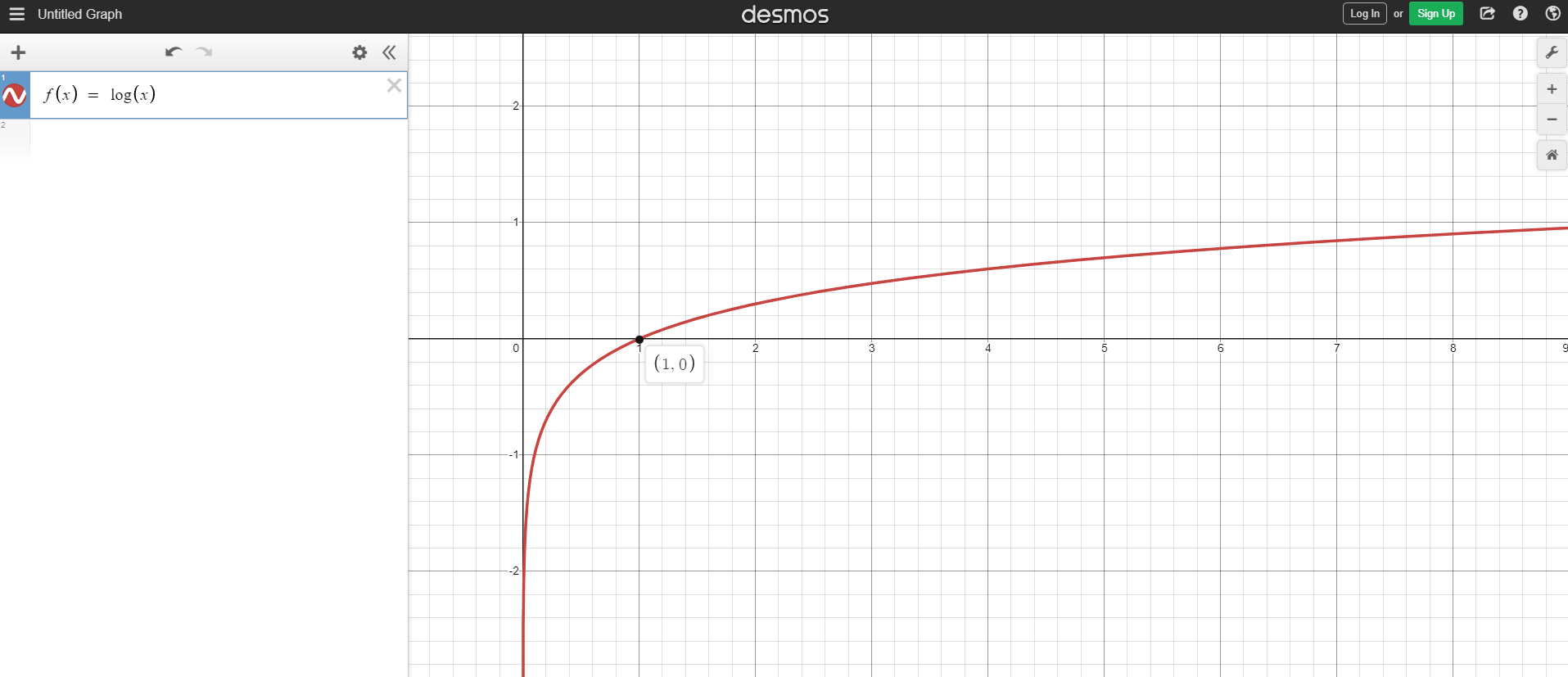
The logarithmic function takes a number input that is more than 0 and gives the logarithm of that number with an associated base. One of the most common bases for logarithms is base 10.
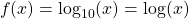
The output is a number y that solves:

or in general with a base:
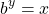
Here are some examples with inputs for the logarithmic function.

Log Function As Inverse Of Exponential Function
A logarithmic function is an inverse function of the exponential function. Think of an inverse function like a reverse or opposite function.
Consider a person flying from Toronto to Shanghai. This is the regular function. An inverse like function here would be the return flight where it is from Shanghai to Toronto.
Here is a math example. g(x) is the main function and we have the inverse function for g.
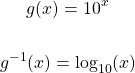
Having two for x in the exponential function gives an output of 100.
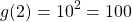
If you put this value of 100 as the input for the inverse function you get back the value of 2. You went from the 2 to 100 with the g(x) function and from 100 to 2 in the g inverse function.
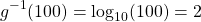
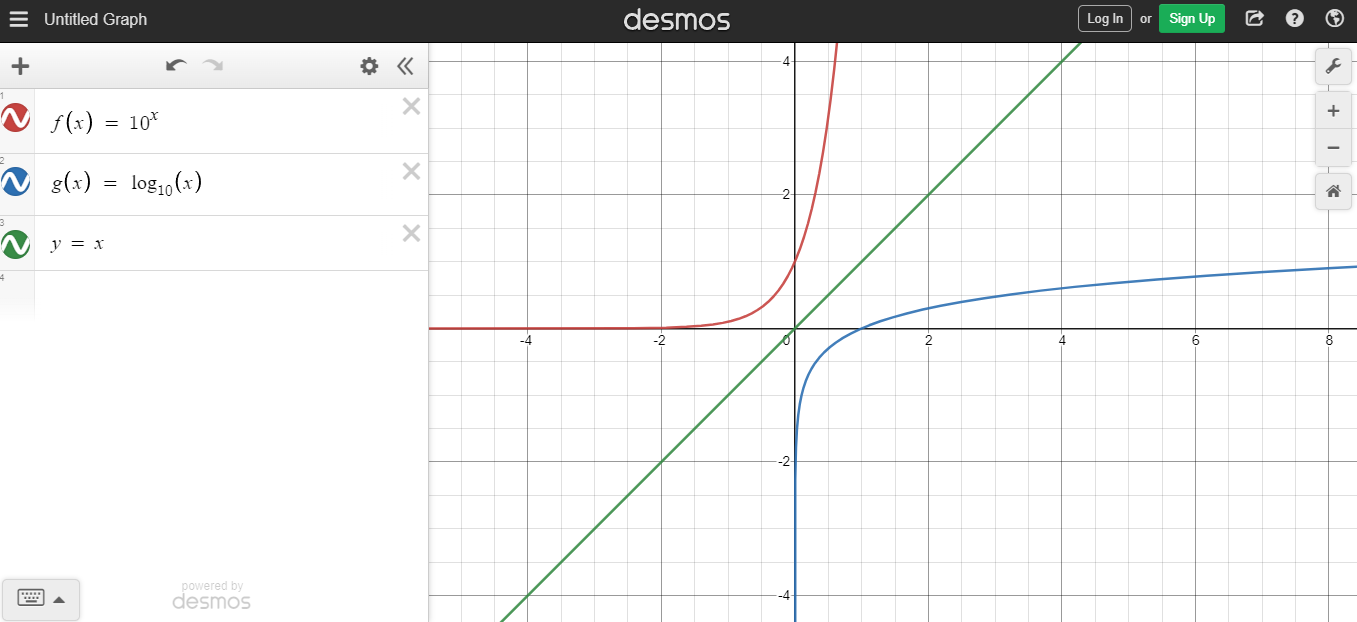
When it comes to graphing and inverses, the original function is symmetric to the inverse function on the y = x line or the 45 degree diagonal line that crosses quadrant 1 and quadrant 3.
Here is a Desmos screenshot.
The green diagonal line is the y = x line. At the top left, that is the exponential function of ten to the power of x. On the bottom right quadrant, that is the logarithmic function of base 10 for an input x.
From a graphing perspective, the inverse of a function on the graph can be obtained with switching the x and y parts of the coordinates with each other. That is (x, y) from the exponential function becomes (y, x) in the log function.
Domain & Range Of Logarithmic Functions
The domain for the logarithmic function is the set of all valid x-values as input for the log function. For the logarithmic function, the domain is all real positive numbers for x. No negative numbers allowed as the input for the logarithmic function as the output would be undefined.
For the range, it is the set of all valid y-values as output for the log function. The range for the logarithmic function is all real numbers.
If you look at the graph for the logarithmic function closely, you will see that the rate of increase is not really big as x gets larger. The math topic of calculus looks at rate of increases more closely which is beyond the scope of this post.
Posted with STEMGeeks