Linear Equations Math Application - Comparing Cellphone Plans
Hi there. In this mathematics based post, I would like to cover an application of using linear equations. Linear equations through algebra and graphing can be used to compare prices on cellphone plans.
Math text is rendered in LaTeX along with the use of QuickLatex.com.

Topics
- Review Of Linear Equations
- An Example Of A Linear Equation
- Comparing Cell Phone Plans - An Example
- What About Paying For The Phone?
Review Of Linear Equations
A linear equation consists of an independent variable x as an input with a dependent variable y as an output. The value m represents the slope of the line. This slope value also represents the increase in y for every 1 unit increase for x.
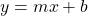
The value of b represents the y-intercept of the line when x = 0.
An Example Of A Linear Equation
Although the main theme in this post is comparing cell phone plans, you can also look at gym membership prices with linear equations.
A local gym charges $30 per month (no tax) on its membership fee with a $20 sign-up fee. What would the graph look like for modeling the price of gym fees from this gym? In addition, what would be the total fees paid to this gym after 12 months?

Table Of Values Approach
| Number Of Months | Fees Paid To Gym At Month # |
|---|---|
| 0 | 20 |
| 1 | 50 |
| 2 | 80 |
| 3 | 110 |
| 4 | 140 |
| 5 | 170 |
| 6 | 200 |
| 7 | 230 |
| 8 | 260 |
| 9 | 290 |
| 10 | 320 |
| 11 | 350 |
| 12 | 380 |
Linear Equation Approach
The amount the gym charges for the membership is thirty dollars per month. This 30 would be the slope and the 20 dollar sign up fee would represent the y-intercept. Let x be the number of months into the gym membership and let y be the total fees paid to the gym after x months.
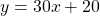
If you wanted to know the amount of total fees paid to the gym after 20 months, replace x with 20 and apply order of operations to compute 620.
Instead of using y, you can adopt the function notation as follows:
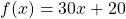
If the number of months in the membership is 5, substitute 5 for x and compute the total fees paid to the gym after 5 months.
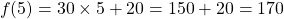
Comparing Cell Phone Plans - An Example
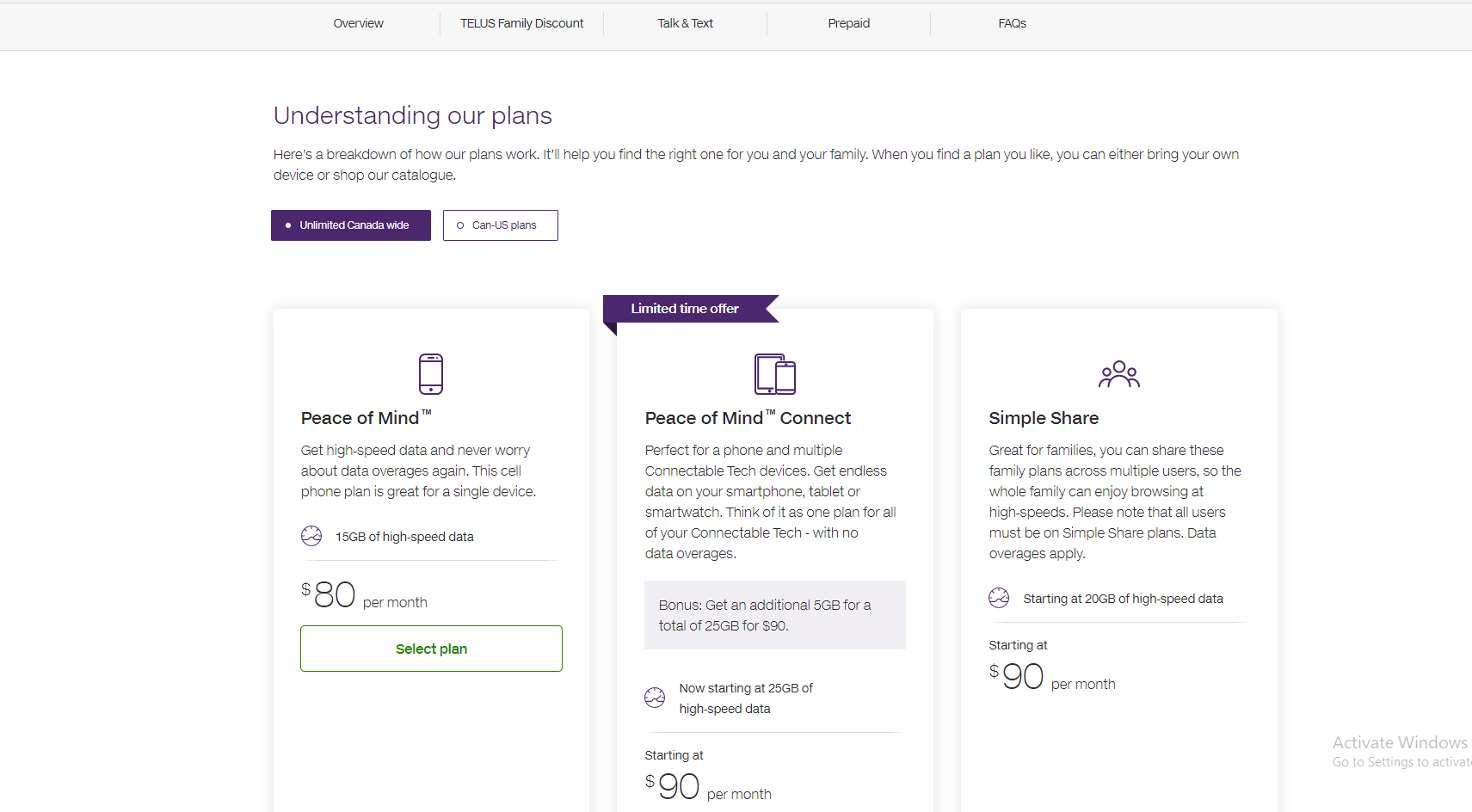
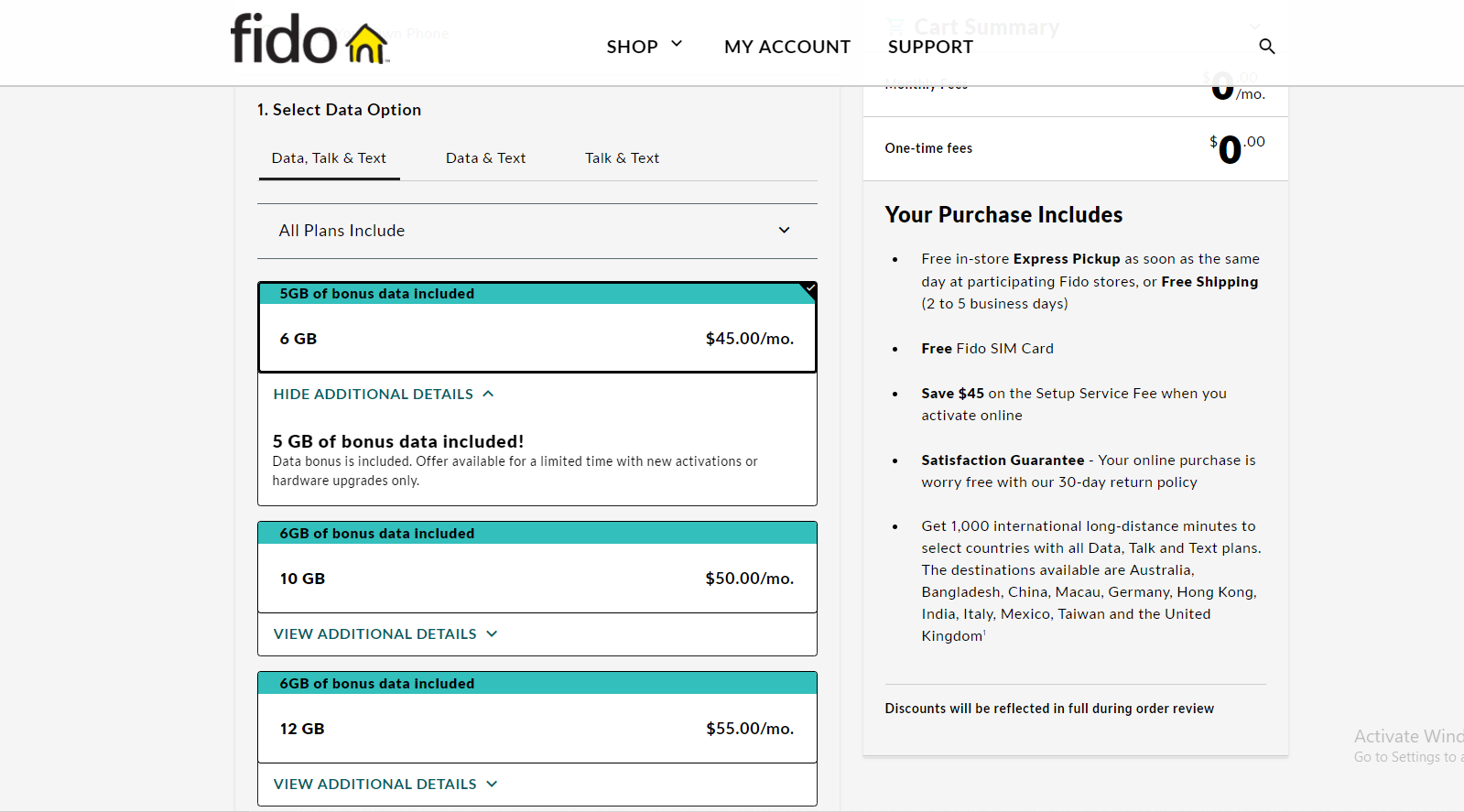
For this example I am comparing cell phone plans between two Canadian telecom providers Telus Mobility and Fido. Cellphone plans in Canada are mostly on two year contracts. I do have screenshots below from their websites.
Telus Screenshot
Fido Screenshot
Telus Peace Of Mind
This Peace Of Mind phone plan from Telus is 80 dollars CAD per month. They advertise getting 15GB high speed data and not worrying about paying overage data fees. Although it is not listed in the screenshot picture, the plan unlimited nationwide calling and texting, unlimited picture and video messaging, call display, call waiting and voicemail.
To model the price as a linear function it would be:
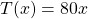
where T is the total fees paid to Telus after x months. There is no y-intercept unless there is a sign-up fee or you pay for the phone.
Fido Build Your Plan - 6GB for $45/mo
There is a cheaper plan from Fido which is owned by parent company Rogers Communications Canada. This plan is $45 a month with 6GB of Data and a 5GB data bonus. There are also other included items that are shown on the right side of the Fido picture screenshot.
The linear function for this Fido phone plan can be modelled by:

with F being the total fees paid to Fido after x months.
Comparing Phone Plans
These phone plans can be compared in terms of price. If comparing by price only, Fido is the winner between the two. There are also factors such as what is included in the phone plans, service coverage, phone device offerings, signal strength, company reputation, taxes, customer service, etc. You could also look at other phone providers and their plans if these two phone plans don't seem convincing. (Costs are in CAD)
| Month Number | Total Fees Paid For Telus Plan At Month # | Total Fees Paid For Fido Plan At Month # |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 80 | 45 |
| 2 | 160 | 90 |
| 3 | 240 | 135 |
| 4 | 320 | 180 |
| 5 | 400 | 225 |
| 6 | 480 | 270 |
| 7 | 560 | 315 |
| 8 | 640 | 360 |
| 9 | 720 | 405 |
| 10 | 800 | 450 |
| 11 | 880 | 495 |
| 12 | 960 | 540 |
After 12 months, the Fido plan is $420 CAD cheaper.
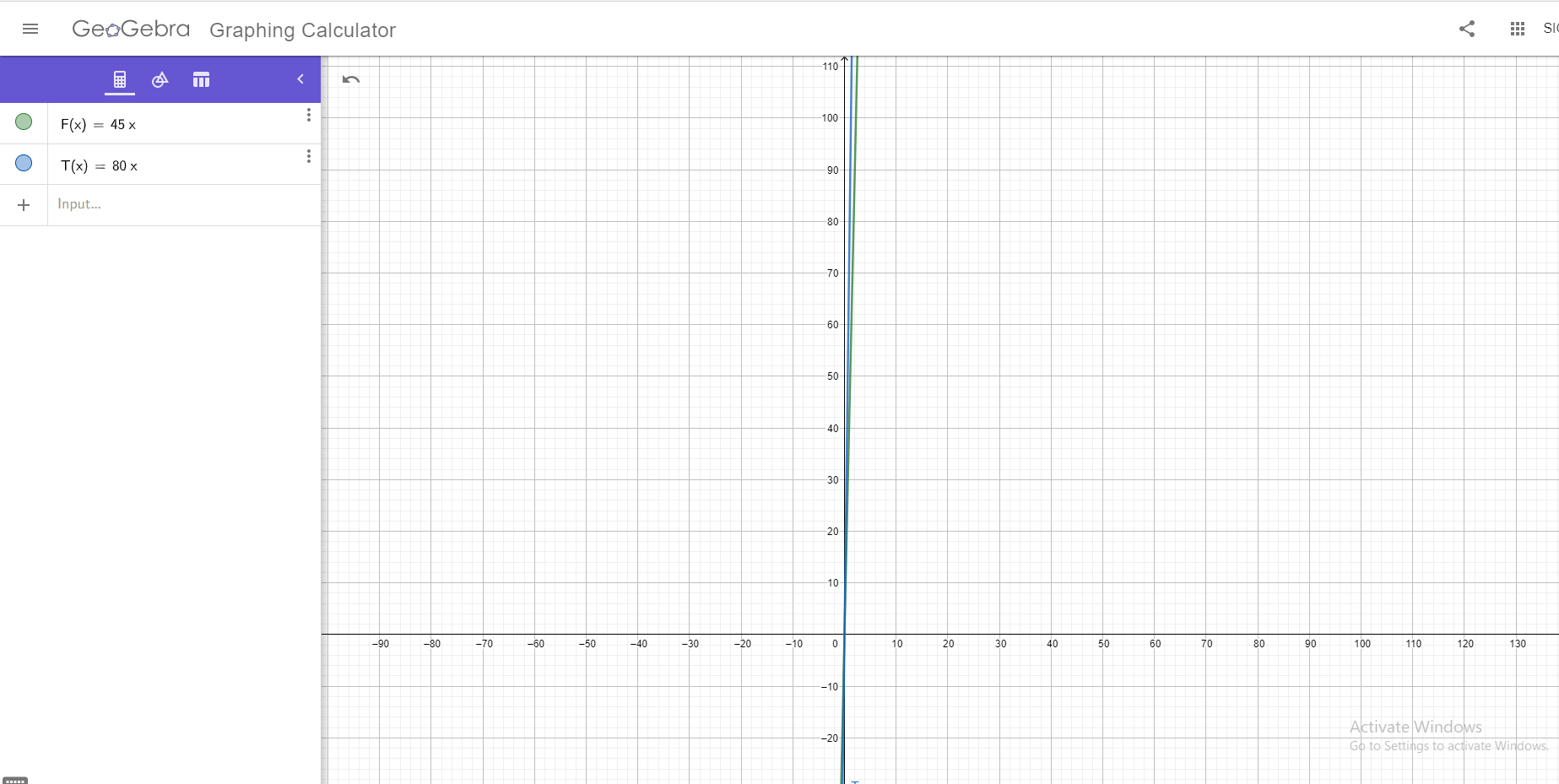
Graphing The Two Phone Plans Linear Functions
You could graph the two linear functions for the two phone plans. It turns out the graph look bad. Here is a screenshot with the use of Geogebra's online graphing calculator. For comparison, use a table of values or evaluate the costs with their linear functions.
What About Paying For The Phone?
The example that is covered here assumes no fees from the phone as you bring your own device (BYOD). If you have to pay for a phone and enter a plan, you would now have a y-intercept equal to the cost of the phone or fees you pay up front.
For example, entering into the Telus plan at $80 CAD per month and paying for one of the latest phones for something like $2200 CAD would be represented by the equation:
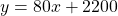
where x is the number of months since starting the plan, y is the total fees paid to the phone company and 2200 is the upfront cost from the phone. The graph for this equation would look like this.
In Canada, there is a common option of not paying for the full phone cost upfront. There is a loan type deal for the phone where you do not pay the full upfront cost but pay more per month on top of the phone plan. That way, you pay off the full cost of the phone in monthly installment payments.

Posted with STEMGeeks