Inverse Relations & Inverse Functions
Hi there. This math education post is on inverse functions.
The math images were found through using the search engine DuckDuckGo. Math text rendered with QuickLaTeX.com.
Topics
- Review Of Functions
- What Is An Inverse?
- Finding Inverses
- Domain & Range Of Inverse Functions
Review Of Functions
A mathematical function requires an input in order to produce a corresponding output. The function applies mathematical algebra with the supplied input to produce an output. Think of it like a vending machine where the input is a certain amount of money in coins. The function would be the pressed button from the user. Once a certain button is pressed, the output being the item from the vending machine dispenses. The vending machine user can now retrieve the outputted item.
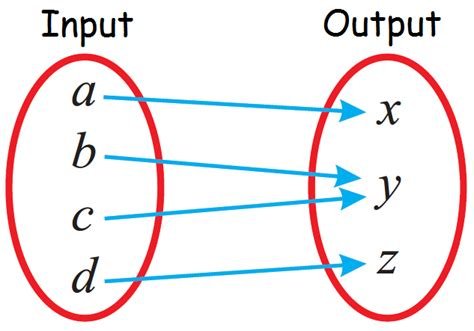
Function Maps
To illustrate how inputs, outputs and functions work a function map is a useful visual. The arrows show which inputs correspond to outputs. Note that different inputs can lead to the same output.
A function must have each input correspond to one output. If there is something where there is at least one input that has two or more outputs, then that is called a relation not a function. A function must have one output for each input.
What Is An Inverse?
When it comes to inverse functions it is now in reverse. The outputs are now the inputs and the inputs become the outputs. Think of it like with flights. The regular function is going from Toronto to New York. Going from New York back to Toronto in the return trip can be compared to the inverse function.
An inverse of a function is a relation. This inverse relation is considered an inverse function if this relation passes the graphical vertical line test. There must be only one output value for each and every input value in the inverse relation.
Finding Inverses
There are two main ways for finding inverses of a function. One is a graphical approach and the second one is an algebraic approach.
Graphical Approach For Determining An Inverse
With a simple linear function such as f(x) = 2x + 1, start with a table of values. For values of x use simple values near 0.
| x | f(x) = 2x + 1 |
|---|---|
| -2 | -3 |
| -1 | -1 |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
These points can be plotted on a grid.
To set up a table of values for the inverse, we switch the x and y values around. The notation for the inverse has a negative 1 which is not to be confused with the exponent of negative 1.
| x |  |
|---|---|
| -3 | -2 |
| -1 | -1 |
| 1 | 0 |
| 3 | 1 |
| 5 | 2 |
| 7 | 3 |
The inverse co-ordinates can be plotted along with the original points on the grid. It is a good idea to good one step further and determine the relation/function that these points are from. This can be done with the algebraic approach from the next section.
In this case the inverse function here is a line. The point-slope form can be determined here.
Using the points (1, 0) and (3, 1) the slope is calculated as follows.
Using the point of (1, 0) and the calculated slope of a half, the point slope form of the inverse function line is:
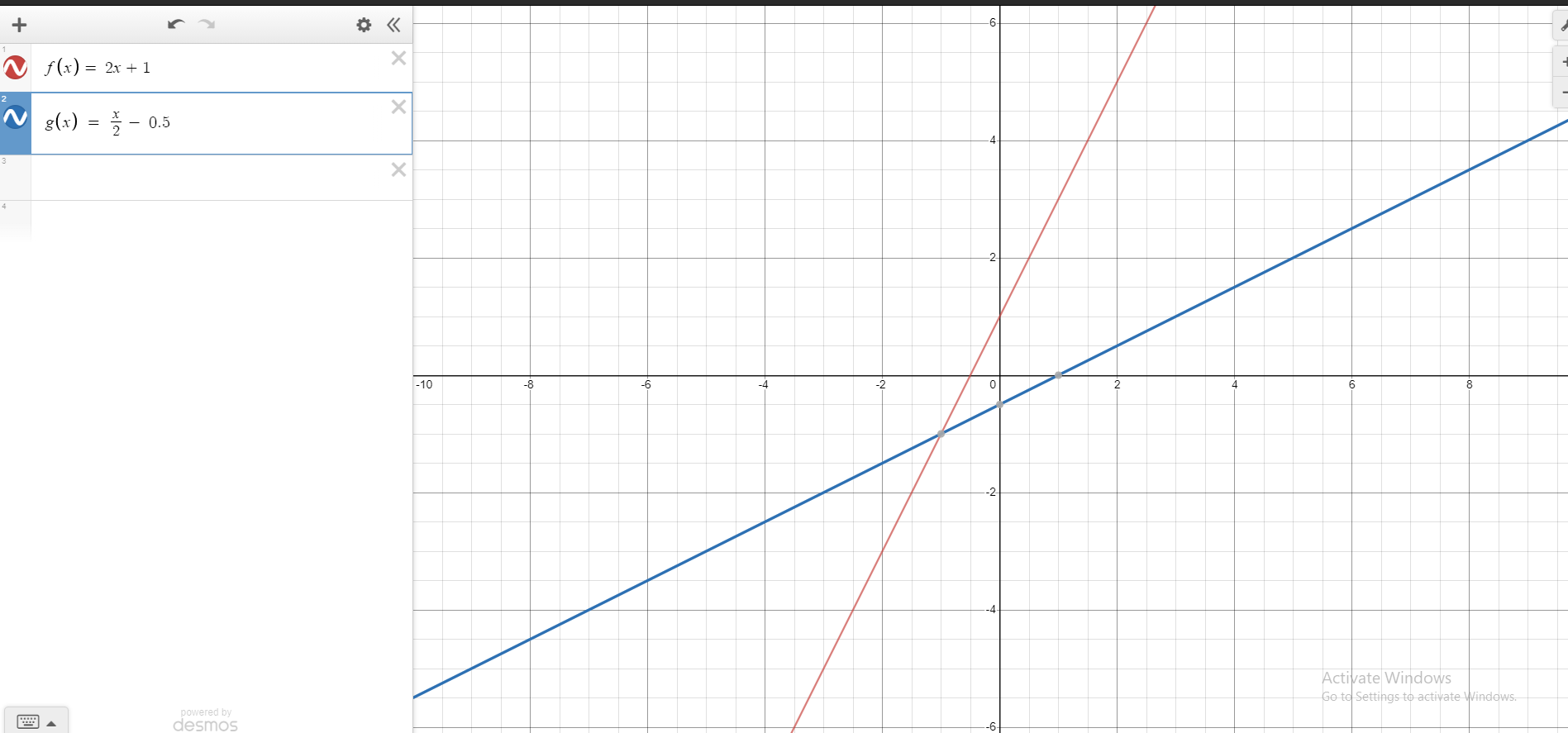
We have the original function of f(x) = 2x +1 and the inverse function of 
. You can graph them together on one grid. You will notice that these two lines are symmetrical of one another. The line of symmetry here is the 45 degree y = x line. The screenshot below is the two lines in Desmos.
Algebraic Approach To Finding An Inverse
The graphical approach is a simple approach for finding the inverse but it does a bit of time. With the graphical approach, you can find the corresponding inverse without spending too much time on graphing. The downside here is working with the algebra.
This example is on finding the inverse of f(x) = 2x + 1. Finding inverses of more complicated functions is possible but I won't include that here.
Given the function f(x) = 2x + 1, I like to replace the f(x) with y. Then I switch the x and y around. This is what you should have.
Solve for this new y and this new y becomes $f^{-1}(x)$. This represents the inverse function given an input of x.
Domain & Range Of Inverse Functions
In a function you have the domain and range of a function. The domain of a function is the set of all valid input (x) values. Function domains do also contain non-valid values or restrictions for a function. The range of a function is the set of all possible or valid (y) output values. As an example the function 
has a domain where any real-valued x-value is valid. The range for the upward facing parabola is y being at least 0.
Remember from the inverse map that the inputs from the original functions are outputs for the inverse function. In addition, outputs from the original function are inputs for the inverse function.
In the context of domain and range this means that:
- Domain of the function is the same as the range of the inverse function.
- Range of the function is the same as the domain of the inverse function.
Simple Example
Consider the function . What is the domain and range for f(x) and its inverse relation.
From earlier it was stated that this parabola has a domain of any x-value or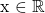 
. The range for the parabola is y being at least 0 or 
with 
.
To find the inverse, first replace f(x) with y. It is now . Switch the x and y variables and solve for y.
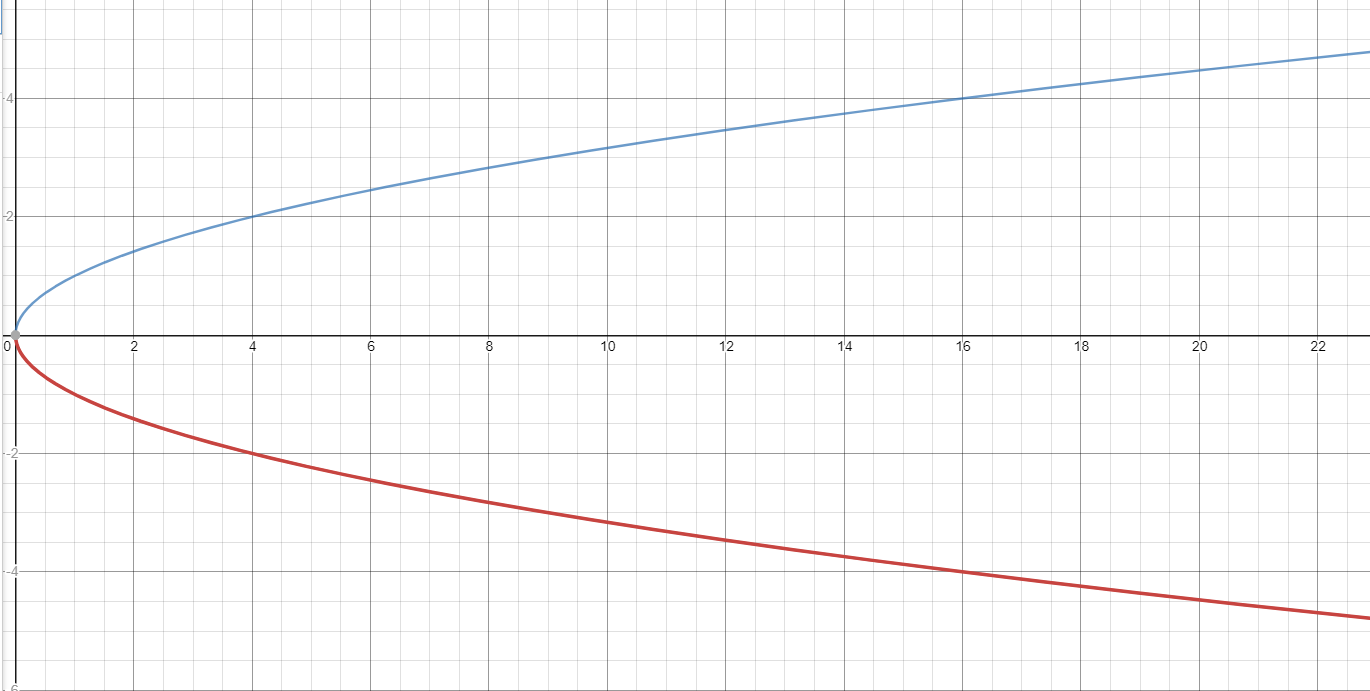
Note that in order for this inverse relation to be a function you could take either one of the minus version or the plus version. If you take both, this inverse is not a function as it fails the vertical line test and there would be two outputs for any x-input.
The screenshot below shows the positive square root function of x in blue and the negative square root part in red. Having both of them at the same fails the vertical line test.
