Introduction To Exponential Functions

Hi there. In this math guide, I introduce the topic of exponential functions. It is assumed that the reader is familiar with exponents.

For math images I use a combination of Quicklatex.com, witeboard.com and my Wacom tablet & stylus.

Pixabay Image Source

 

Topics

---

• The Exponential Function
• Determining Exponential Function From Table Of Values

 

The Exponential Function

---

The exponential function takes an exponent input and produces an output. How the input is used to produce an output is based on the following function.

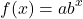
where b is the base number, x is the exponent and a is the y-intercept. The output is f(x) which depends on the value of the exponent x.

If the function is 2 to the power of x you would have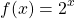

 

From the function f(x) if the exponent was 1 the output would be 2 to the power of 1 which is 2. An exponent of 5 would give two to the power of 5 which is 32.

 

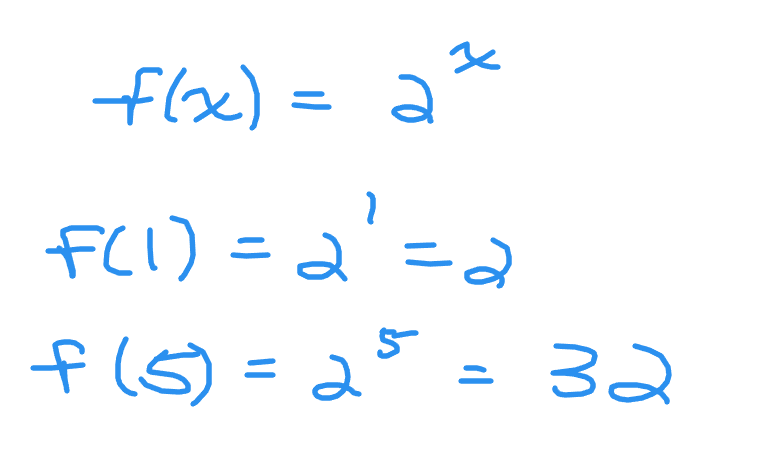
If the exponent is x = -2 you would have two to the power of negative two. This would be one divided by two to the power of two which gives 1/4.

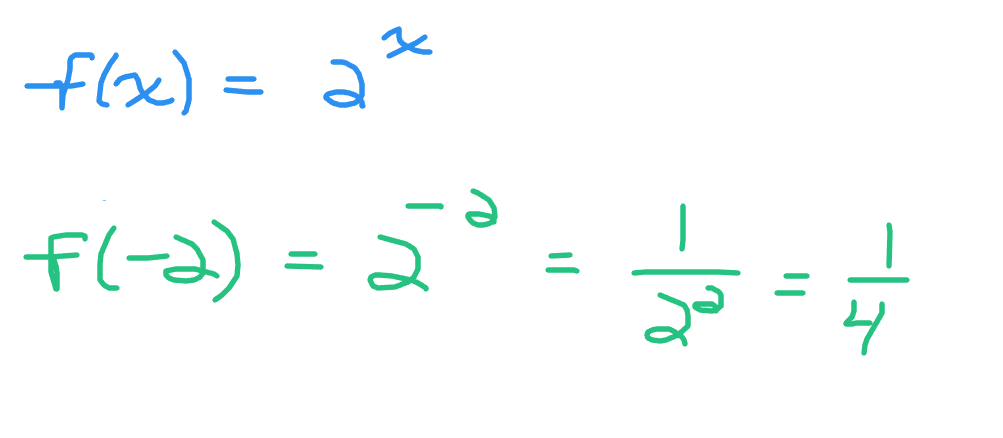
We can develop a small table of values.

x	f(x) = 2^x
-2	1/4
-1	1/2
0	1
1	2
2	4
3	8

 

Determining Exponential Function From Table Of Values

---

The previous section dealt with obtain values once the exponential function is known. What if you have the opposite case? That would be using some inputs and outputs from an exponential function and finding the exact equation for it.

Example One

x	y
-2	1/9
-1	1/3
0	1
1	3
2	9
3	27

 

The y-intercept here is 1, so a = 1.

For every time that x increases by 1, y increases by a multiple of 3 (or multiply by 3 each time x increases by 1). This multiple of 3 represents the base (b). The exponential equation for this example would be y = 3^x. Screenshot below.

 

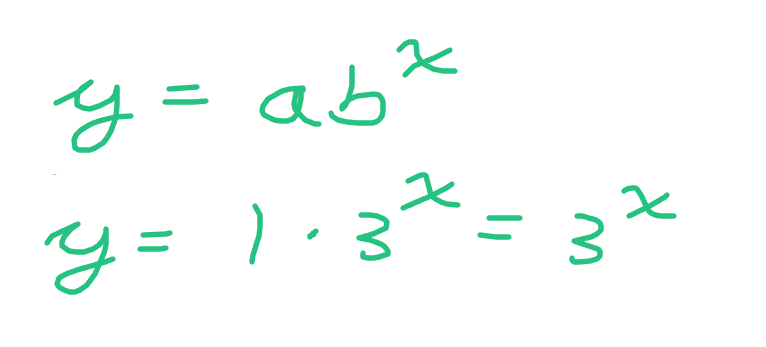
Example Two

x	y
-2	-
-1	1
0	2
1	4
2	8
3	16

 

From the table above, the y-intercept is 2. This is the y-value when x is equal to 0. The a-value from the exponential equation here is 2.

Whenever x increases by 1, y increases by a multiple of 2. The base value b in the exponential equation is 2.

 

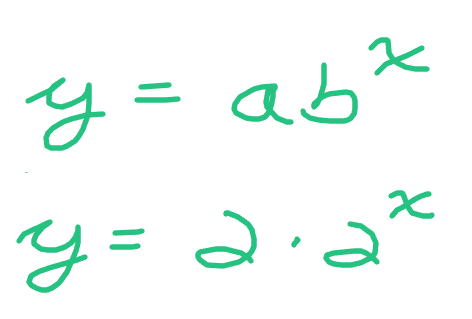
Example Three

x	y
-2	16
-1	4
0	1
1	1/4
2	1/16
3	1/64

In this table the y-intercept is 1. As x increases by 1, the y-value decreases by dividing by 4. Dividing by four is the same as multiplying by one-quarter. The base value here is one-quarter in the exponential equation.

 

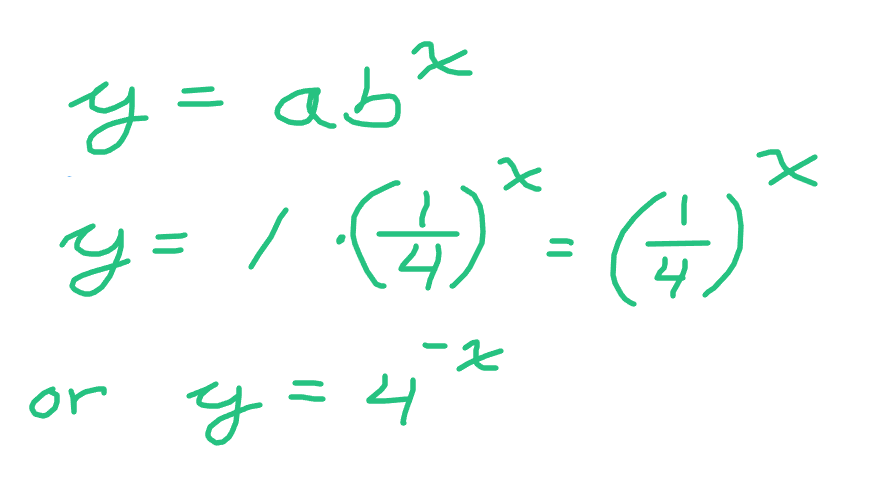
Example Four - Only One Point Known

This fourth example is slightly different. Other than the y-intercept there is only one known point from the exponential equation. Algebra is used to find the pieces of the exponential function.

x	y
-2	-
-1	-
0	1
1	-
2	4
3	-

 

From the exponential equation y = ab^x, substitute the known point (2, 4) along with a = 1. The value of a is 1 as this number one is the y-intercept. After substituting x = 2 and y = 4 solve for the value of b.

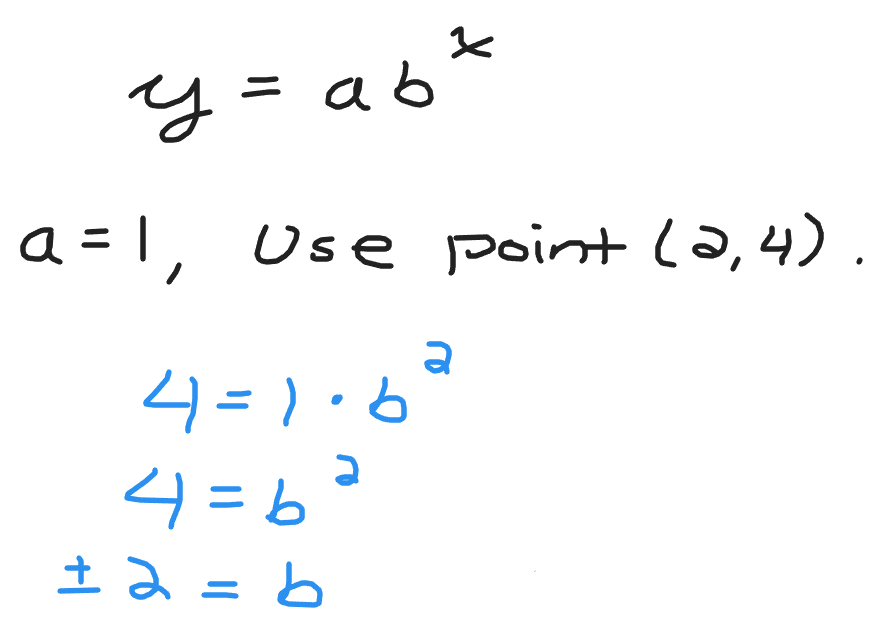
The value of the base b can be either positive two or negative two. If the base is a negative then you do not really have an exponential function as the signs alternate between positive and negative depending on the exponent being even or odd. Take the positive two to obtain the exponential function of to the power of x.

 

Thank you for reading.

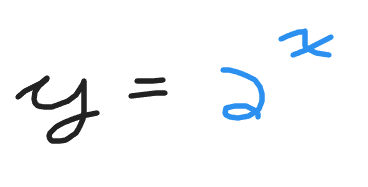
Posted with STEMGeeks