Greatest Common Factor (GCF) Of Numbers With The Cake Method
Hi there. In this math education post, I cover the topic of greatest common factor of two or more numbers with the cake method. It is sometimes called the ladder method.

Topics
- What Is A Greatest Common Factor?
- Cake Method
- Online Tools & Related Math Games On GCF
What Is A Greatest Common Factor?
Before getting into the concept of a greatest common factor, it is a good idea to review the concepts of factors and common factors.
A factor is typically a whole number that is used for multiplication. Factors of 6 are 1, 2, 3 and 6. Six times one makes 6 and two times three equals to 6 as well. The number 1, 2, 3 and 6 are numbers that can be used for multiplication to make six. As an another example, the number 10 has factors of 1, 2, 5 and 10. We have 1 x 10 = 10 and 2 x 5 = 10 or 5 x 2 = 10.
Common factors are factors that are common between two numbers. Earlier we have the numbers of 6 and 10. Factors of 6 are 1, 2, 3 and 6 and factors of 10 are 1, 2, 5 and 10.
Two and one are common factors for 6 and 10. The greatest common factor (GCF) here is 2 as it is the largest common factor.
Another Example
What is the greatest common factor for 9 and 15?
The greatest common factor for 9 and 15 is 3.

Cake Method
The method shown above for obtaining the greatest common factor required listing factors. This method is simple to follow but it may not be the fastest. The above method could be slow or even difficult if the numbers become really large.
A good method for determining the greatest common factor between two or more numbers is the cake method. It is sometimes called the ladder method as well.
I use https://www.tutorialspoint.com/whiteboard.htm and screenshots for the images here.
Example One
Find the greatest common factor (GCF) of 24 and 30.
With the cake method start with this setup (screenshot below). The two numbers are listed at the top with an L shape.
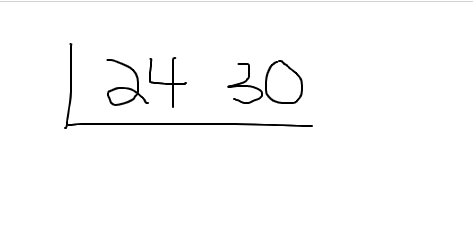
Determine a common factor that is in 24 and 30. It does not have to be a large number factor. You can do something as simple as 2 as both 24 and 30 are even. Write the 2 on the left side of the L shape.

As the 2 is used as a common factor, divide 24 by this 2 and divide 30 by this 2. The numbers of 12 and 15 are in the next layer.
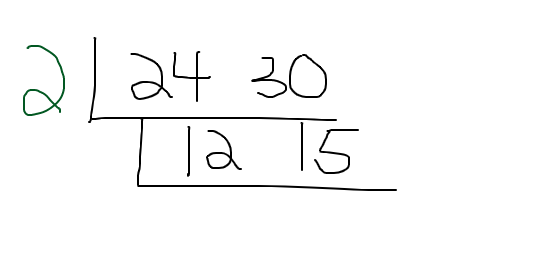
There is a common factor greater than one between 12 and 15. That is 3. Write the 3 on the outside of this second layer.
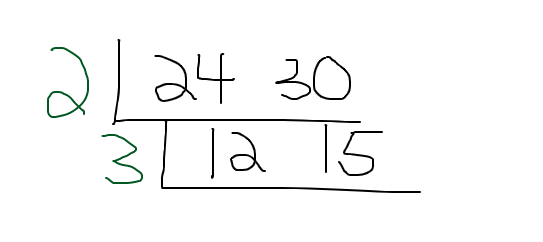
Divide 12 by 3 and divide 15 by 3 to obtain 4 and 5.
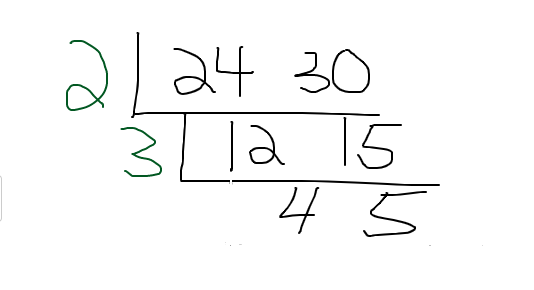
As the greatest common factor between 4 and 5 is 1, there is no need to draw another L layer. We are done. The greatest common factor is the product of the left side numbers. This is two times three to get 6.
The GCF between 24 and 30 is 6.
Example Two
Find the greatest common factor (GCF) of 28 and 112. I display the full cake method screenshot for this example.
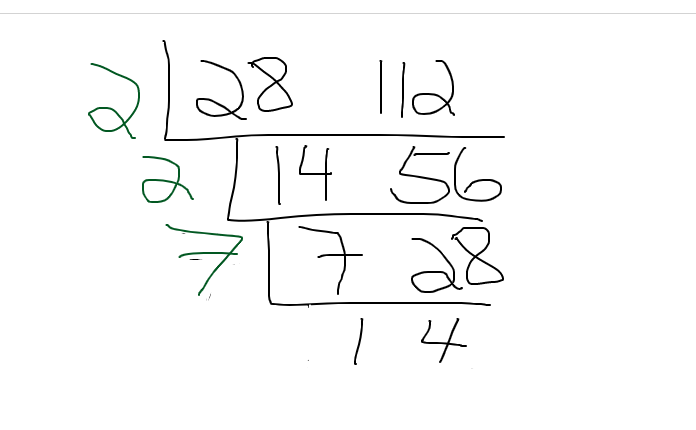
Example Three - Three Numbers Case
What is the greatest common factor (GCF) between 180, 90 and 300?
For dealing with three numbers, the cake method is not that much different. There is just an extra number involved. Start with the setup as follows.
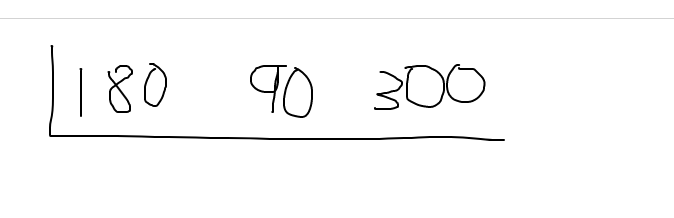
Determine a common factor between the three numbers. You do not have to select a large common factor. Choose something that is obvious for you. You can choose 3 but I chose 10 as each of three numbers are multiples of 10.

Divide all three numbers in the L shape by 10. The next layer has the three numbers of 18, 9 and 30.
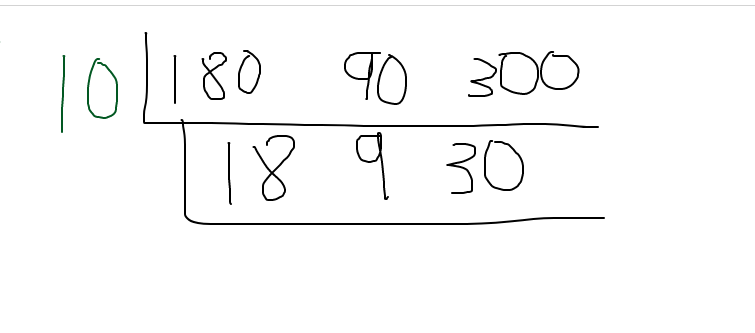
Select another common factor here. Three is a factor for all three numbers. Place the three on the left side and divide all three numbers by 3 to obtain the next row.

From the three numbers of 6, 3 and 10 there is no common factor for all three numbers. We are done here. The greatest common factor (GCF) here is 10 x 3 = 30.

Online Tools & Related Math Games On GCF
There are some neat online tools and math games that relate to Greatest Common Factors. Here are a few that I have found on the internet.
- Madformath.com GCF Cake Method Calculator - Two Numbers
- Madformath.com GCF Cake Method Calculator - Three Numbers
- Multiples & Factors Game
- Mathkite - Greatest Common Factor (GCF) Game

Posted with STEMGeeks