Finding Lowest Common Multiples (LCM) With The Cake Method
Hi there. In this mathematics post I cover the concept of the lowest common multiple or LCM for short with the use of the cake method. The cake method helps with visualizing numbers and obtaining lowest common multiples.
The lowest common multiple is the smallest possible number that two or three numbers go into. As one example, six is the lowest common multiple for 2 and 3.

Topics
- Review Of Multiples & Common Multiples
- Cake Method With Examples
Review Of Multiples
The concept of multiples can be related with the multiplication times tables. As an example multiples of 3 are 3, 6, 9, 12, 15, 18 and so on. Multiples of 3 are from the 3 times tables. Multiples of 5 would be 5, 10, 15, 20, 25, 30 and so on.
Common Multiples
When it comes to dealing with 2 numbers we can have common multiples.
Multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 and so on.
Multiples of 5 are 5, 10, 15, 20, 25, 30 and so on.
A common multiple of 3 and 5 is a multiple that is in both 3 and in 5. Common multiples of 3 and 5 are 15, 30, 45, 60 and so on. The lowest common multiple (LCM) between 3 and 5 is 15.
Another Lowest Common Multiple Example
What is the lowest common multiple between 4 and 36?
Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40 and so on.
For the number 36, multiples of 36 are 36, 72, 108 and so on.
The lowest common multiple between 4 and 36 is 36.

Cake Method With Examples
Listing multiples of numbers can take time when it comes with obtaining the lowest common multiple between two numbers. If the numbers are large, listing multiples and finding common multiples can take a bit of time.
The cake method is a neat visual method that helps with finding lowest common multiples. It is easier to use the cake method as it does not require a high level of number sense to use it. However you do need to have familiarity of common factors (not covered here).
I use screenshots from https://www.tutorialspoint.com/whiteboard.htm.
Example One
What is the lowest common multiple between 8 and 12?
For starting the cake method write 8 and 12 at the top. Place a L from the top left to the bottom right of the 12.
Find a common factor that goes into both 8 and 12. You could go as simple as 2 but I am taking 4. Four is the greatest common factor.
For the next row do 8 divided by 4 to get 2 and 12 divided by 4 to get 3.
There is no common factor other than 1 for the numbers 2 and 3. We stop here. The lowest common multiple (LCM) for 8 and 12 is the product of the 4 on the left along with 2 and 3 on the bottom. That is 4 times 2 times 3 to get 24.
Example Two
Determine the lowest common multiple for 60 and 100.
As both 60 and 100 are even numbers you can start with a common factor of 2.
The next row is 30 and 50 from 60 divided by 2 and 100 divided by 2.
Use 2 as the common factor to obtain the next row of 15 and 25.
A common factor other than 1 that goes into 15 and 25 is 5. The next row would be 3 and 5.
There is no common factor between 3 and 5 that is not 1. Mutliply 2, 2, 5, 3 and 5 to obtain 300. Three hundred is the lowest common multiple for 60 and 100.
Example Three - Three Numbers
We can extend the cake method to three numbers.
What is the LCM for 10, 15 and 20?
Start with the first row and use the common factor of 5.
The next row is 2, 3 and 4. A common factor that applies to two of the three numbers in the row is 2. Two goes into 2 and 4.
Divide 2 by 2 to get 1, 4 divided by 2 gets 2 and leave the 3 alone.
The lowest common multiple of 10, 15 and 20 is the product of 5, 2, 1, 2, 3. Multiply these five numbers to obtain the LCM of 60.
Posted with STEMGeeks

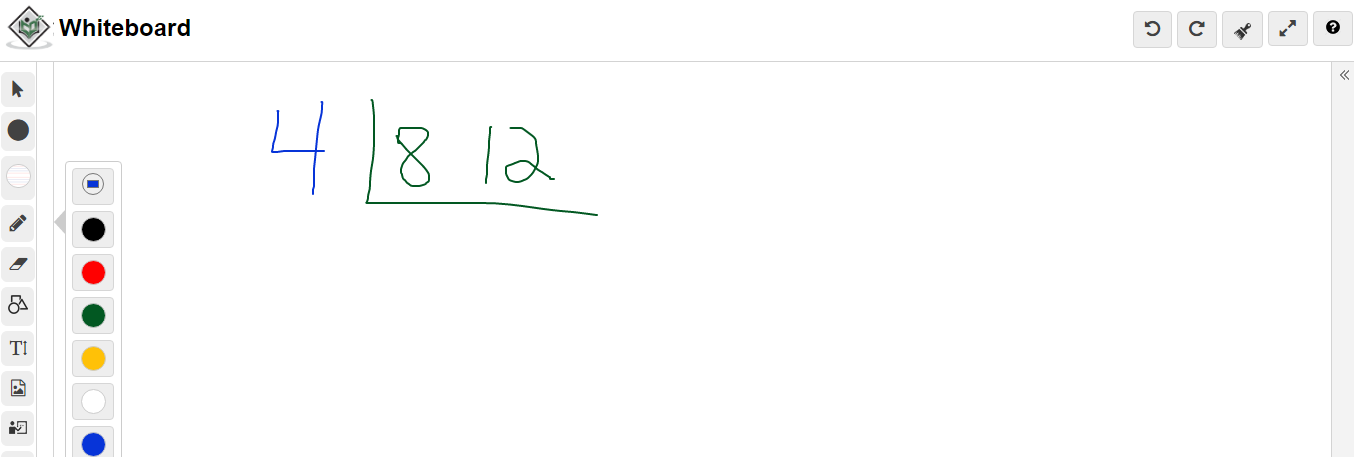



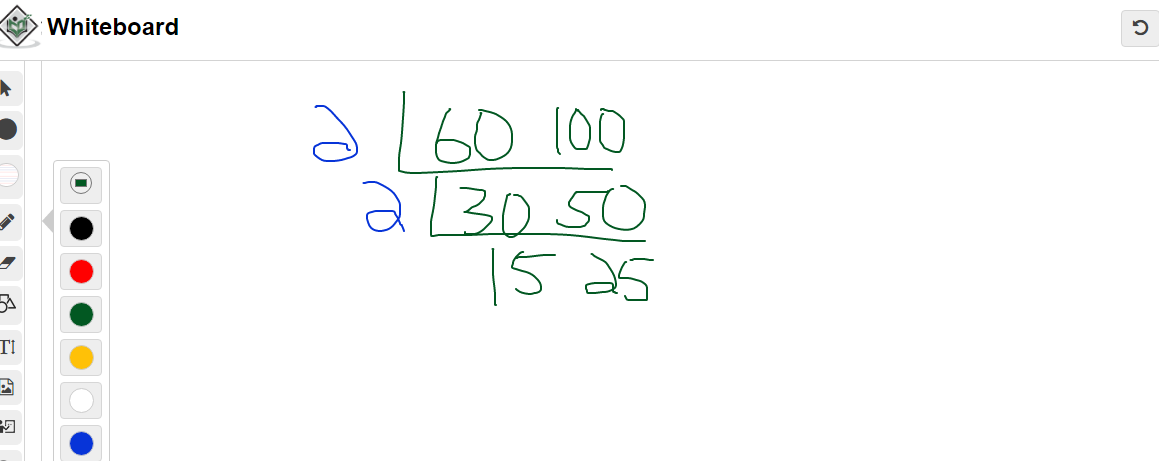
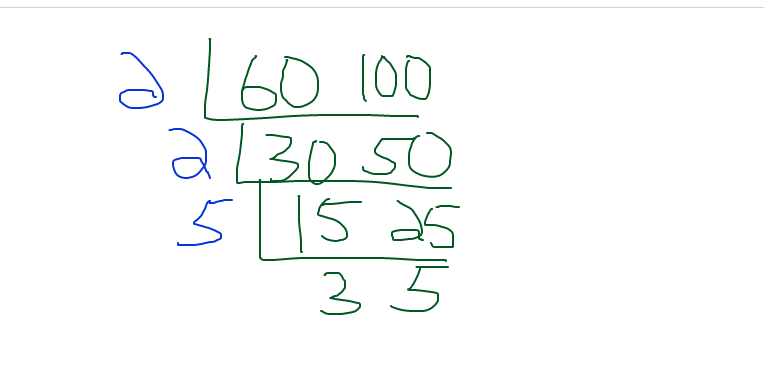

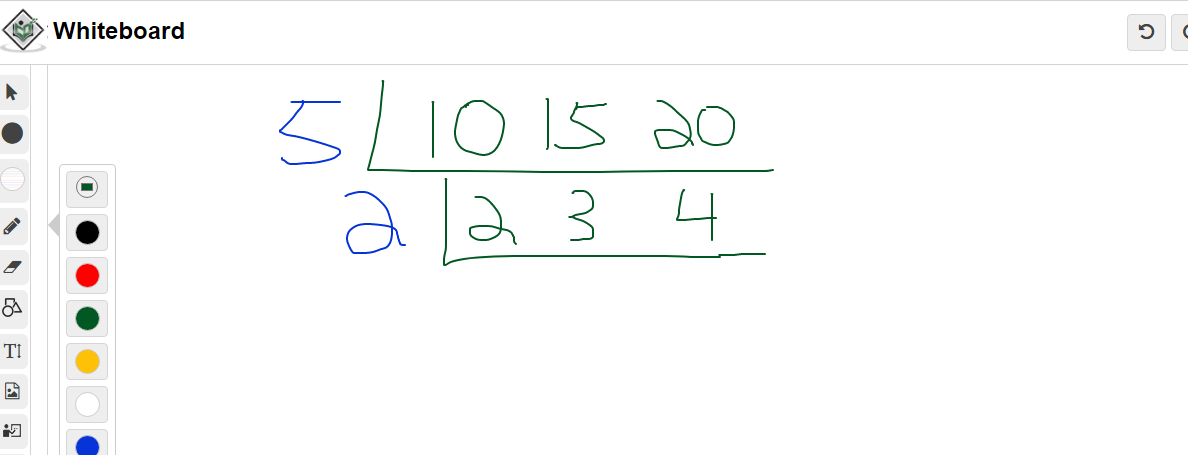
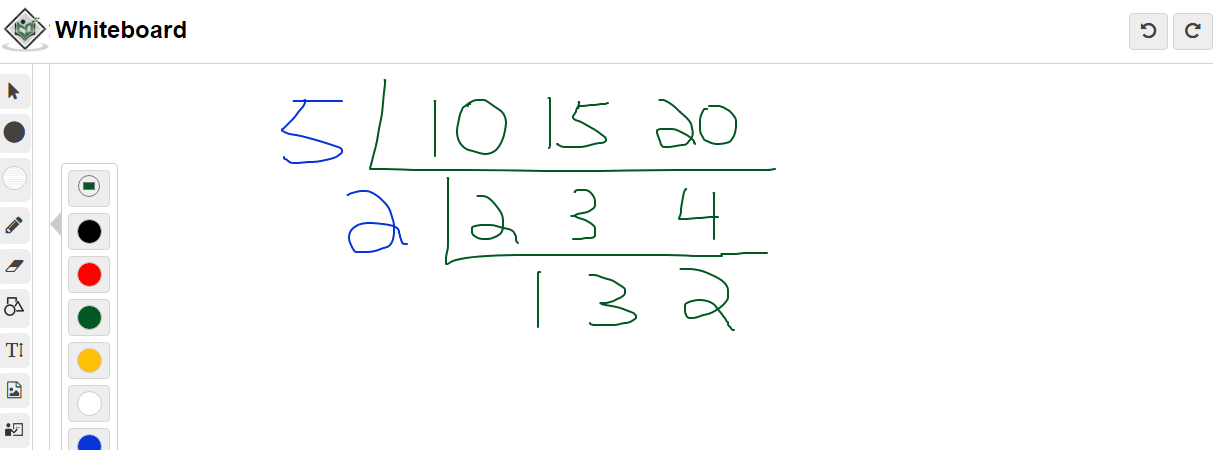
Nice keep it up.
if you haven't receive 300 HIVE and 200 LEO than vote LeoFinance for witness
LeoFinance is a well known and great project so i am vouching for it
Vote for LeoFinance and get 300 HIVE and 200 LEO now
CLICK HERE TO VOTE NOW
@cve3 Your comment contains a link that is on my blacklists ❗ ❗ ❗ 1 2 3
@dkmathstats do NOT click on the link above in their comment.
Reason: PHISHING
Link: "jaro69fuck.top*" => DO NOT CLICK ❗
More info: https://hive.blog/hive/@keys-defender/new-feature-phishing-detection-and-auto-reply
Comment 10% downvoted to make it less visible.
This message is self-voted to be more visible among others.
DO NOT FOLLOW any instruction and DO NOT CLICK on any link in the comment!
Great work and thanks for making maths easier :) !1UP
You have received a 1UP from @mango-juice!
@stem-curatorAnd they will bring !PIZZA 🍕
Learn more about our delegation service to earn daily rewards. Join the family on Discord.
It's a nice thing learning this method of finding the lowest common multiples. Thanks for sharing this informative content with us!