Euclid's Algorithm For Finding The Greatest Common Factor Of 2 Numbers
Hi there. In this mathematics post, I cover Euclid's algorithm for finding the greatest common factor (gcf) between two numbers.
Euclid's algorithm falls under the number theory side of mathematics.
Quicklatex.com is used for math text and LaTeX rendering.

Topics
- Greatest Common Factors Review
- Euclid's Algorithm With Examples
- Practice Problems
- Solutions To Practice Problems
Greatest Common Factors Review
Before getting into greatest common factors, it is important to start with number factors and then common factors.
Number Factors
As an example, factors of 8 include 1, 2, 4 and 8 itself. This is because you can have 1 x 8 = 8 and 2 x 4 = 8. The numbers 1, 2, 4 and 8 can be used in multiplication to obtain 8.
Factors of 20 would be 1, 2, 4, 5, 10 and 20. We have 1 x 20 = 20, 2 x 10 = 20 and 4 x 5 = 20.
Common Factors Between Two Numbers
When it comes to two numbers or even more, you can find common factors between them. Consider the numbers 12 and 21.
Factors of 12 are 1, 2, 3, 4, 6 and 12.
Factors of 21 are 1, 3, 7 and 21.
The common factors of 12 and 21 are 1 and 3.
Greatest Common Factor
The greatest common factor would be simply be the largest common factor. From the above example the greatest common factor is 3.

Euclid's Algorithm With Examples
Euclid's Algorithm is a procedure that helps determining the greatest common factor between two numbers. The greatest common factor (gcf) is sometimes referred to as the greatest common divisor (gcd).
Instead of going through the general case for Euclid's algorithm, I think it is better to show how this algorithm works with examples.
Example One
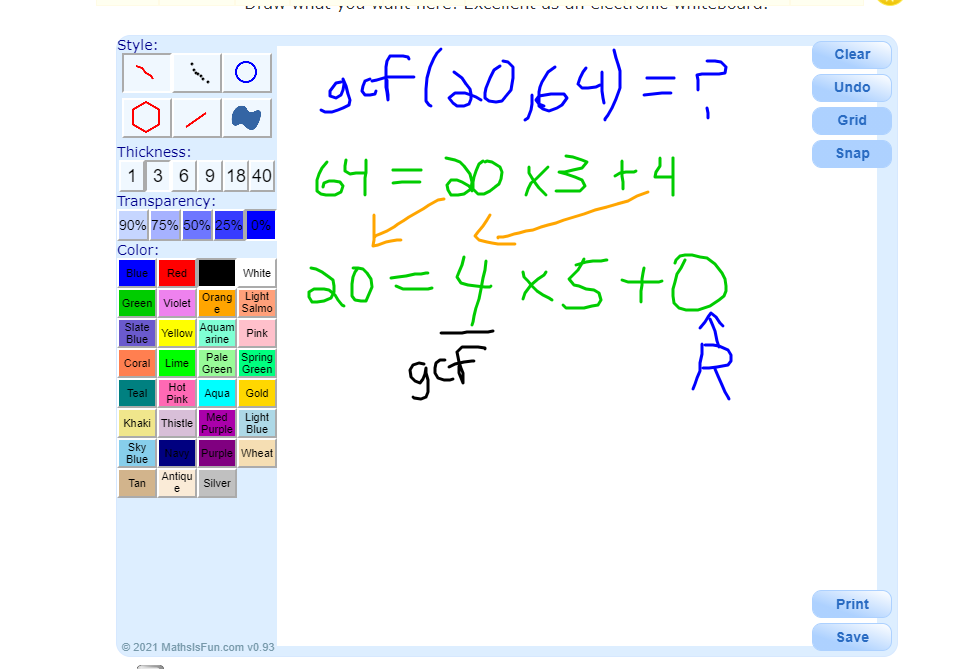
What is the greatest common factor between the numbers 20 and 64?
The larger of the two numbers is 64. This 64 would be on the left side of the equation. Express this larger number 64 as a multiple of the smaller number 20 plus a remainder.
You could also do 64 divided by 20 to obtain 3 with a remainder of 4.
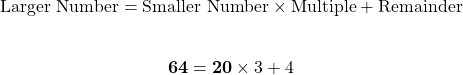
For the next equation, the left side is 20 which was the smaller number. The right side uses the remainder 4 from the previous equation multiplied by a multiple plus a remainder.

Euclid's algorithm stops when the remainder is 0. The greatest common factor here is 4 for 20 and 64. I have included a screenshot below as a summary. (Mathisfun Whiteboard part of website is used)
Example Two
Find the gcf of 122 and 180.
The first line for Euclid's algorithm would be 180 being equal to a multiple of 122 plus a remainder.
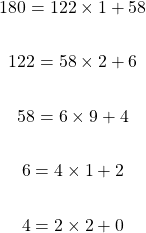
The gcf of 122 and 180 is 2.
Example Three
What is the gcf of 228 and 750?
Start with 750 on the left side. Express 750 as a multiple of 228 with a remainder.
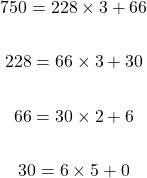
Six is the greatest common factor of 228 and 750.
For those who want a more detailed and theoretical view of Euclid's algorithm, consider this page.

Practice Problems
For each question, find the greatest common factor or greatest common divisor for the two given numbers.
17 and 51
32 and 52
102 and 260
1021 and 222
Solutions To Practice Problems
gcf(17, 51) = 17gcf(32, 52) = 4gcf(102, 260) = 2gcf(1021, 222) = 1
Posted with STEMGeeks
I've never learned the name of this method and yet done this throughout school. lol
Lol.
Maybe the teachers did not know the method. They just taught it.
Ha probably. I had a lot of younger teachers in my time through public school.
Your posts are really well constructed and laid out but may I make a suggestion please as most of your readership here are 'big children'. Firstly, could you give us a few real-world examples of why we might want to know the subject of a post and secondly, please post the answers to the solutions of the practice problems in your next post!
Best wishes and please don't take this comment as a criticism in any way.