Determining The Point Of Intersection Of Linear Equations
Hi there. In this math post I cover the topic of the point of intersection from two lines or two linear equations. It is assumed that the reader is familiar with solving linear equations.

Topics
- Equation Of Line Review
- Point Of Intersection Visual Examples
- Solving For Point Of Intersections Algebraically
Equation Of Line Review
In the math & algebra framework a line contains a slope, a y-intercept, an input which is usually the variable x and an output variable which is usually y. The output y depends on the input variable x. A y-intercept is a y-value when x is equal to 0. The slope is a numerical value which is a measure of the rate of change. For every one increase in the input x, the output y increases by this slope amount.
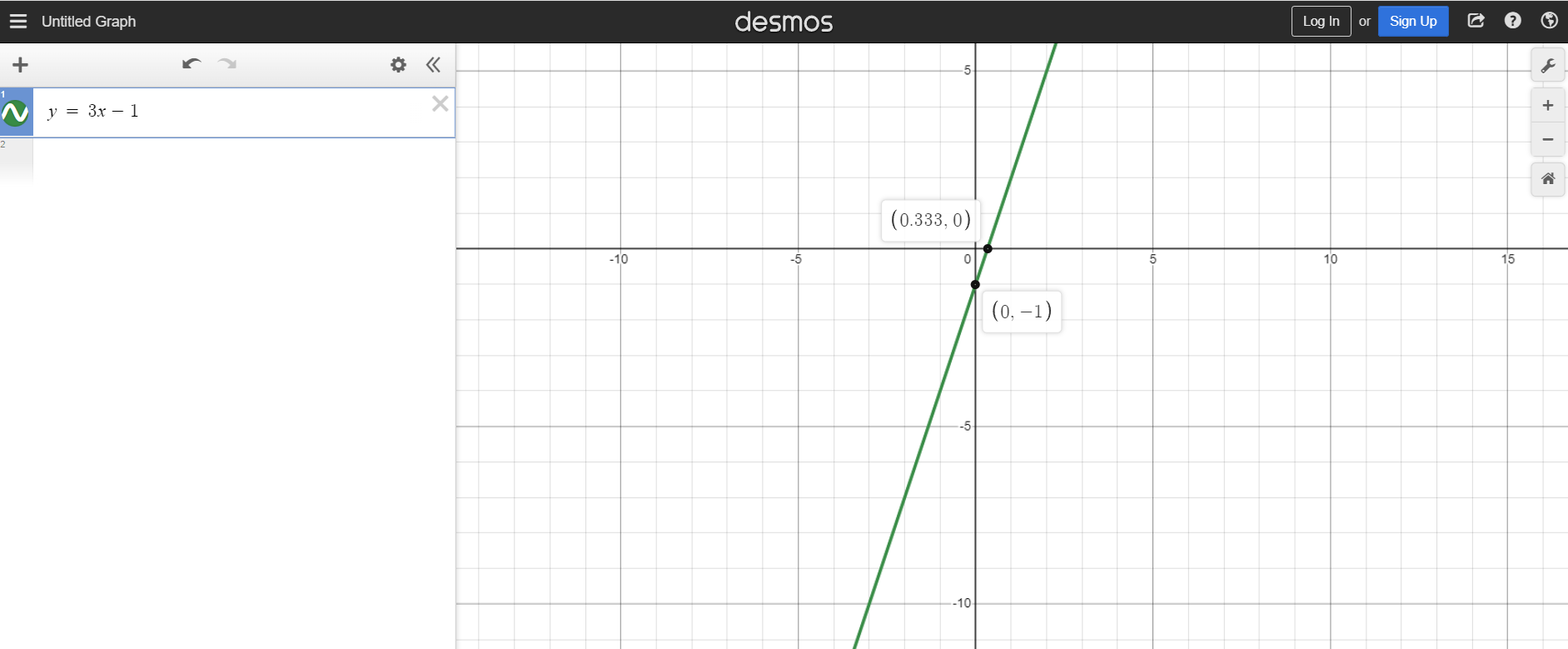
Example One: y = 3x - 1
With this first example we have y = 3x - 1. The input variable is x and the output variable is y. The slope is the number in front of x is 3. This three means that when x increases by one the output value increases by three. Negative one would be the y-intercept.
Desmos graph screenshot shown below.
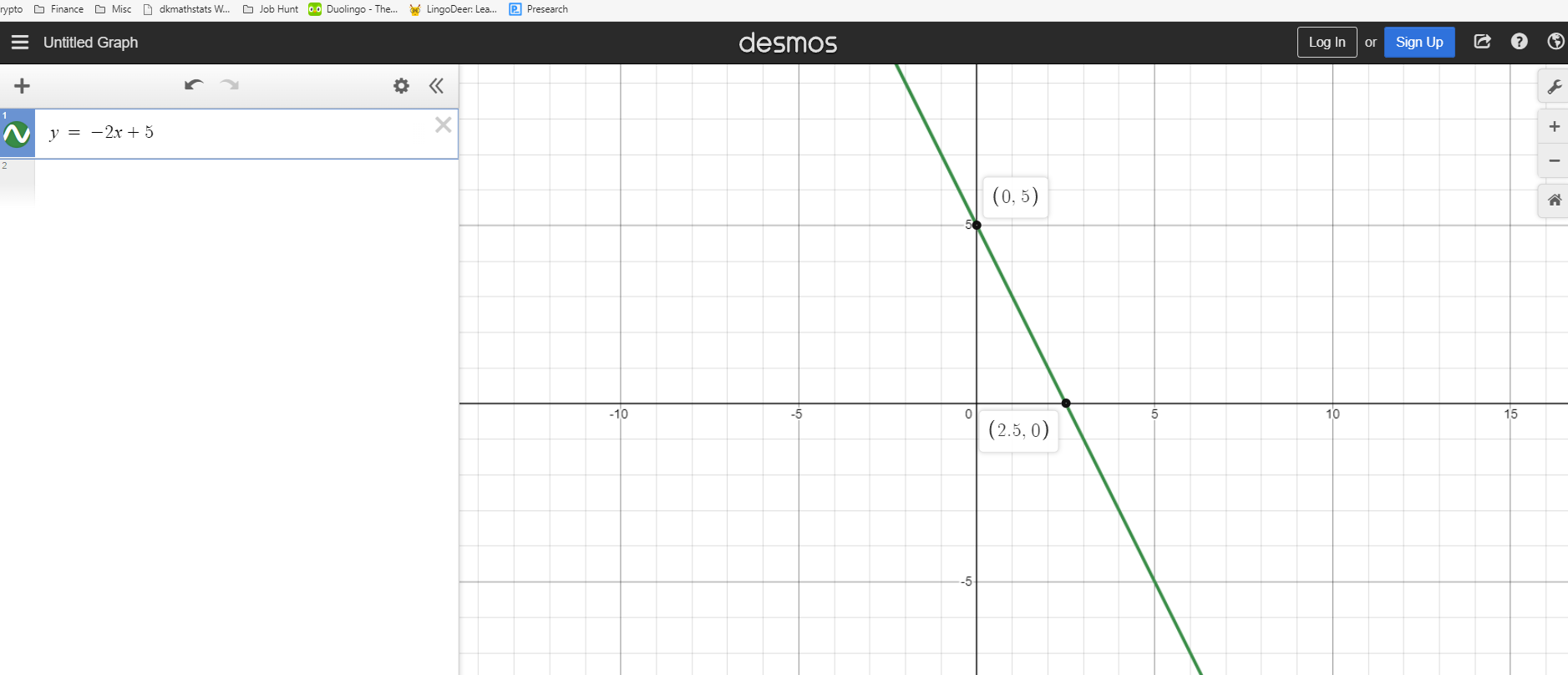
Example Two: y = -2x + 5
This example is different as the slope is negative with a negative 2. A negative slope of -2 means that for every increase of 1 for x, the output y decreases by 2. The y-intercept here is a positive five.
Point Of Intersection Visual Examples
When two lines are plotted on the (x, y) coordinate grid you have one of three cases.
- One point of intersection between the two lines
- No points of intersection as both lines are parallel to each other.
- Infinitely many points of intersection from the two lines.
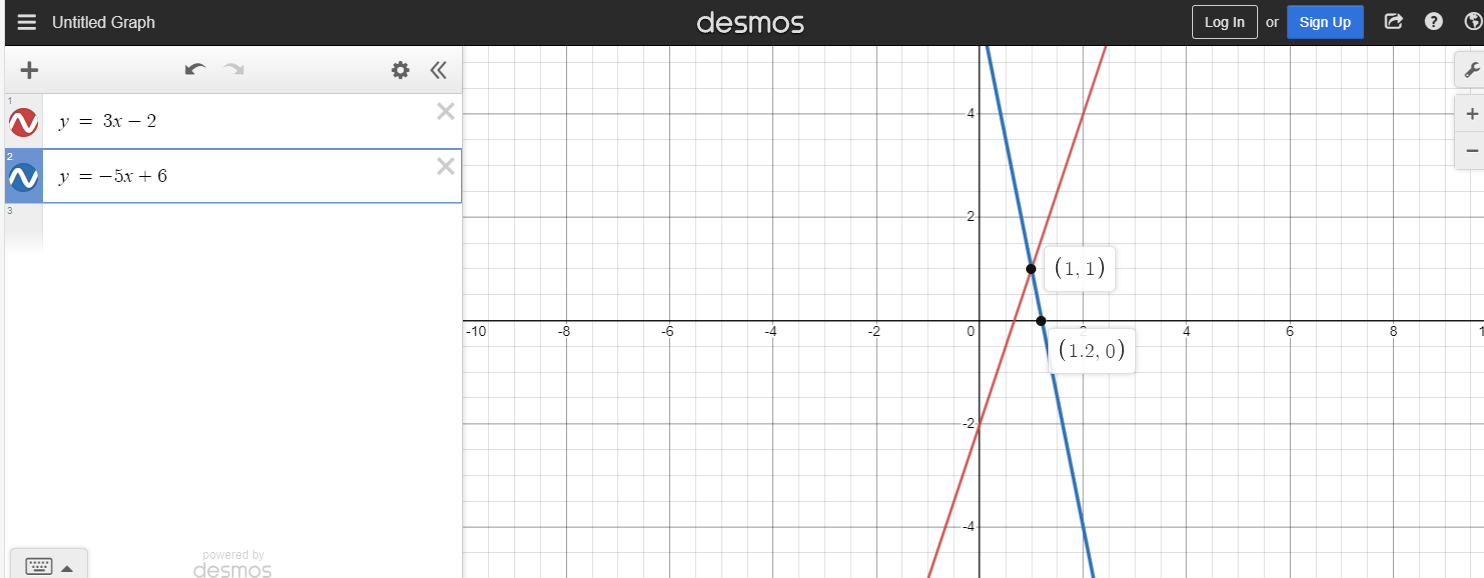
Case One - One Point Of Intersection
Suppose there are two lines where the first line is y = 3x - 2 and the second line is y = -5x + 6. The first line is in red and the second line is in blue from the Desmos screenshot image below.
The point of intersection of these two lines is the (x, y) point (1, 1). The red line is below the blue line when is x less than 1. When x is greater than 1 the red line is above the blue line.
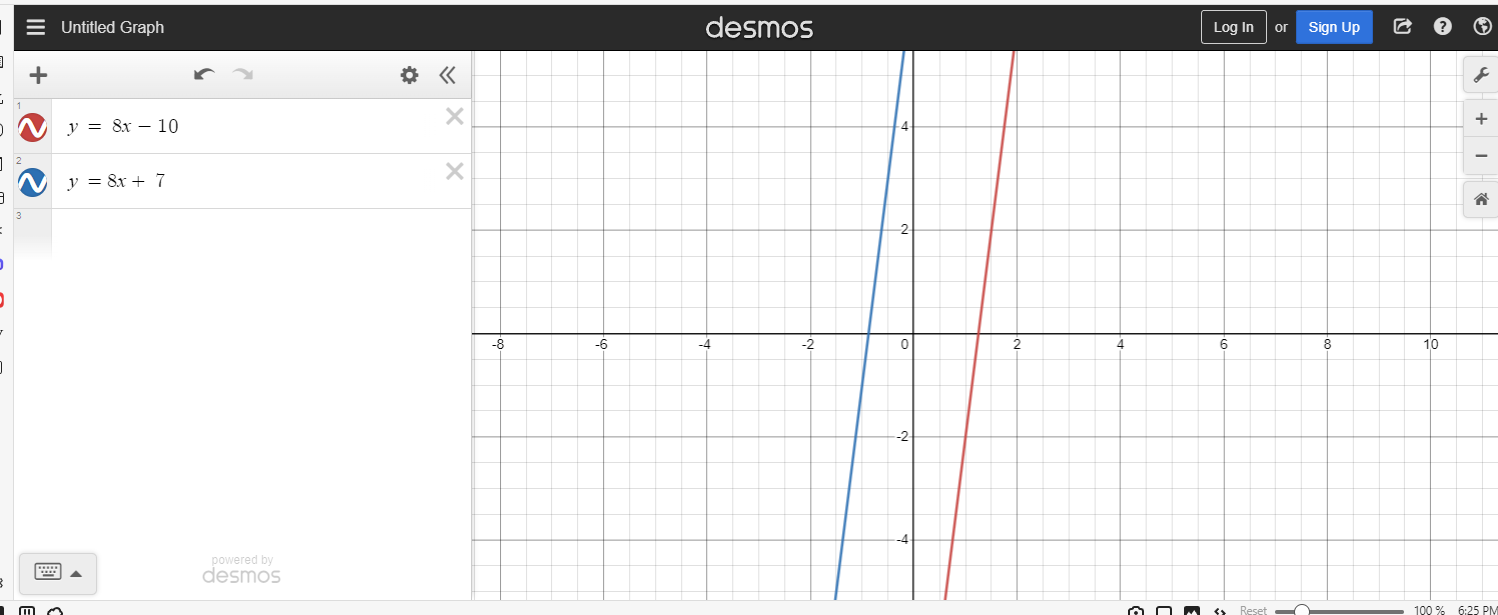
Case Two - No Points Of Intersection
If you have something like y = 8x - 10 in red and y = 8x + 7 in blue, these two lines do not intersect or touch each other.
Why is this the case from a mathematical perspective? The red line has a y-intercept of negative ten and the blue line has a y-intercept of seven. What these two lines have in common is that they both have the same slope of eight. A no points of intersection case occurs with the two lines when the slopes are the same and the y-intercepts are different.
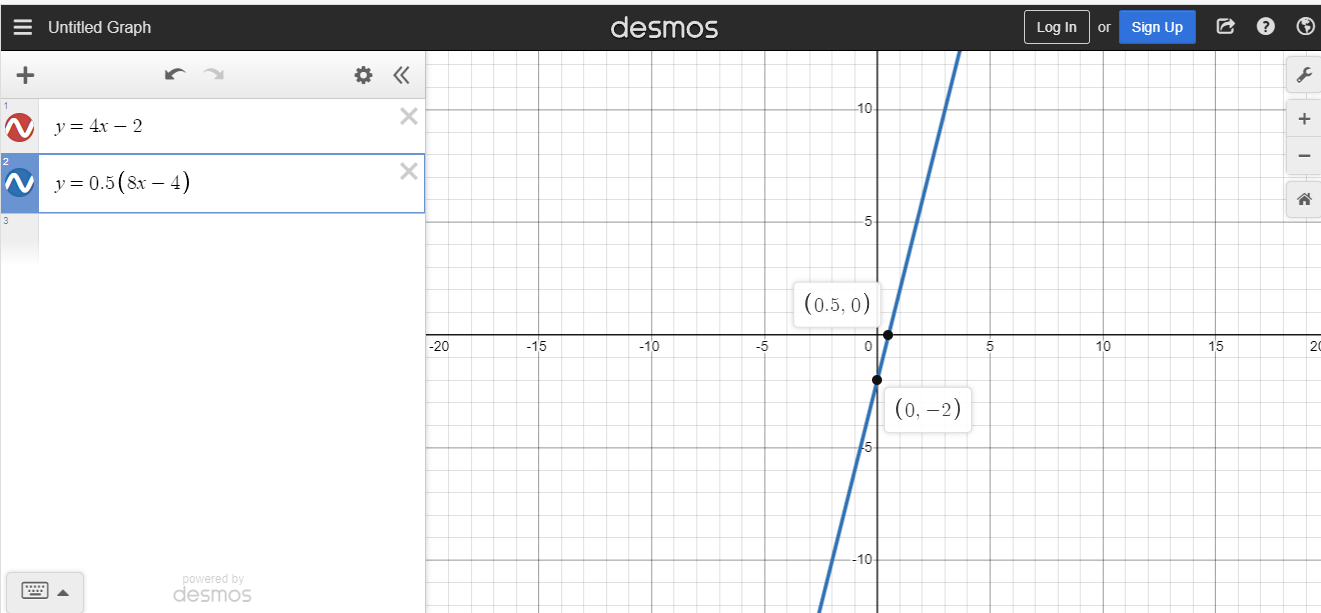
Case Three - Infinitely Many Points Of Intersection
When two lines have the same slope and the same y-intercept then two lines are the same. These two lines would be on top of each other and have infinitely many points of intersection. If the word infinite is scary think of an unlimited number of points of intersection for this case.
In the screenshot below I use y = 4x - 2 in red and y = 0.5(8x - 4) in blue. The blue line is the same as you get the same red line after taking half of 8x and half of -4.
Solving For Point Of Intersections Algebraically
When it comes to the algebraic method of solving linear systems there are two methods that you can use to find the point of intersection. These two methods are substitution and the elimination method. For these examples I use the substitution method.
Example One
Find the point of intersection for y = 3x - 1 and y = x + 5.
Both of these equations are in the form of y = something. As long as one of the equations is in the form of y = you can replace y in the other equation with the first equation.
In this case you can replace the y from y = x + 5 with 3x - 1.
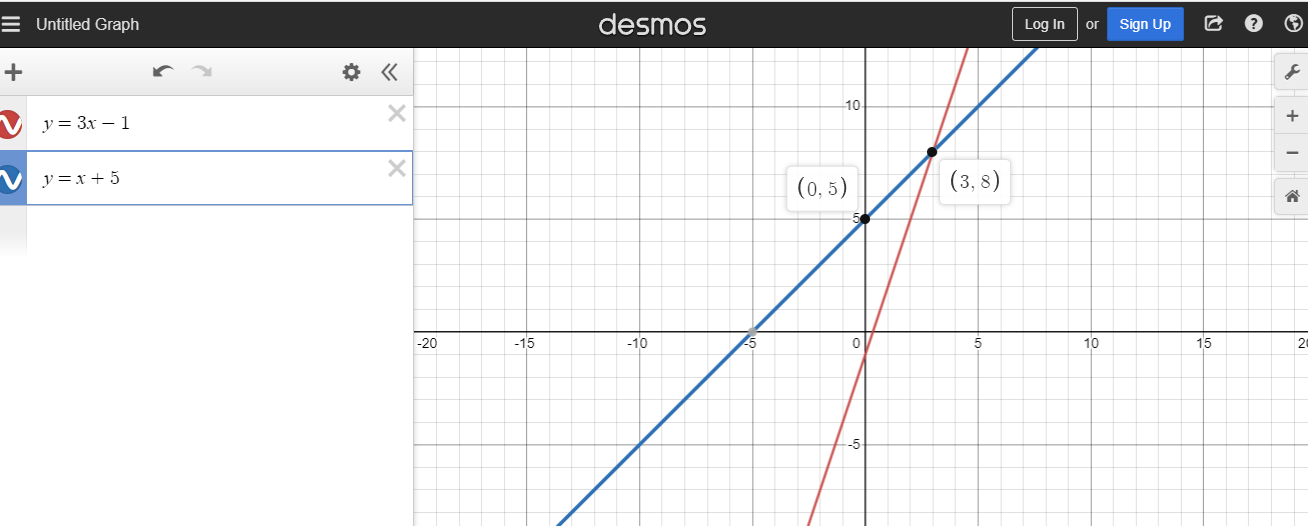
You have 3x - 1 = x + 5. Have the terms with x on one side and the numbers on the other side. The left side would be 3x - x which is 2x. The right side would be 5 + 1 which is 6. Solve for x in 2x = 6. The value for x is 3. Use the value of 3 for x in y = x + 5. Three plus five gives eight, the value for y.
The point of intersection here is (3, 5) Screenshots included below.
Example Two
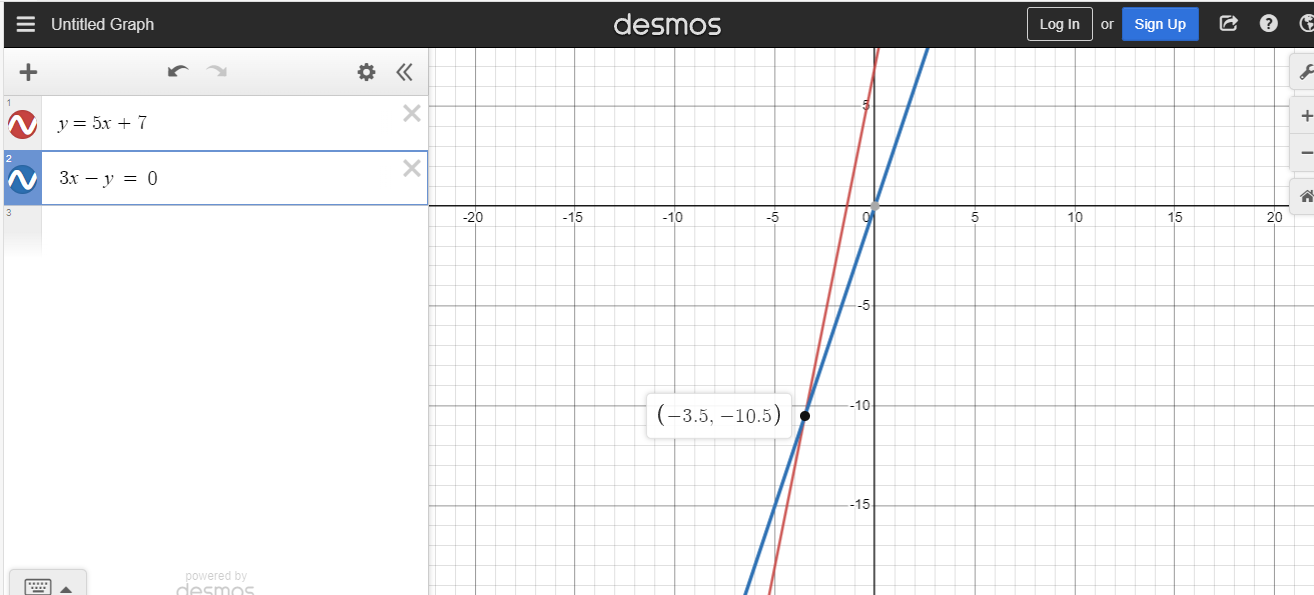
In y = 5x + 7 and 3x - y = 0, determine the point of intersection.
One of the two equations is in the y = something format. This is good. Replace the y from 3x - y = 0 with 5x + 7. You would then have 3x - (5x + 7) = 0. Distributive the negative through each term in the bracket. The result would be 3x - 5x - 7 = 0 which simplifies to -2x - 7 = 0. Rearrange to obtain 2x = -7 Solve for x to obtain x = -3.5 or -7/2.
Use x = -3.5 in y = 5x + 7. The value of y would be 5 x -3.5 + 7 = -17.5 + 7 = -10.5 The solution or point of intersection here is (-3.5, -10.5).
Example Three
Find the point of intersection for 2x + y = 0 and 2x - y = 2.
Both of these equations are not in the y = something form. Choose one of the equations and isolate for y. Once that is done use the substitution method and solve for the point of intersection.
From the first equation you can rearrange 2x + y = 0 into y = -2x. Replace y from 2x - y = 2 with -2x. The result would be 2x - (-2x) = 2 which simplifies to 4x = 2. The value of x would be half. Use the value of half for x in 2x + y = 0. This would be 2(0.5) + y = 0 or 1 + y = 0. The value of y is negative one. (0.5, -1) would be the point of intersection here.
Posted with STEMGeeks
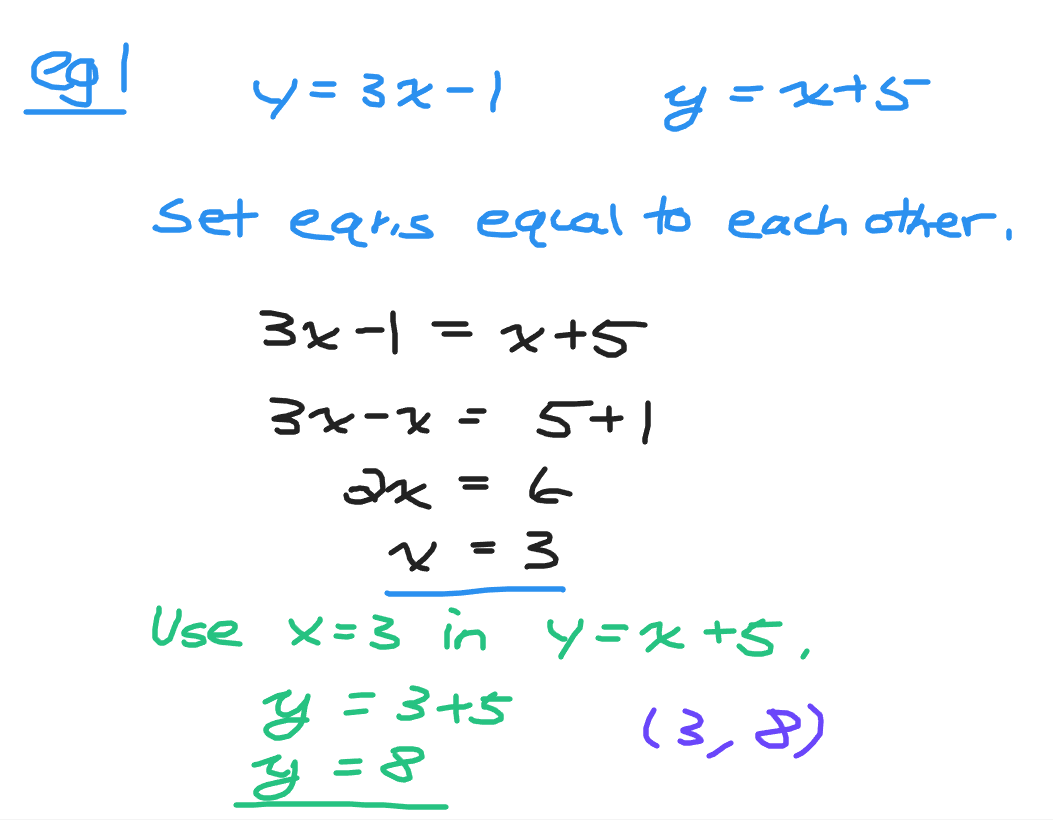
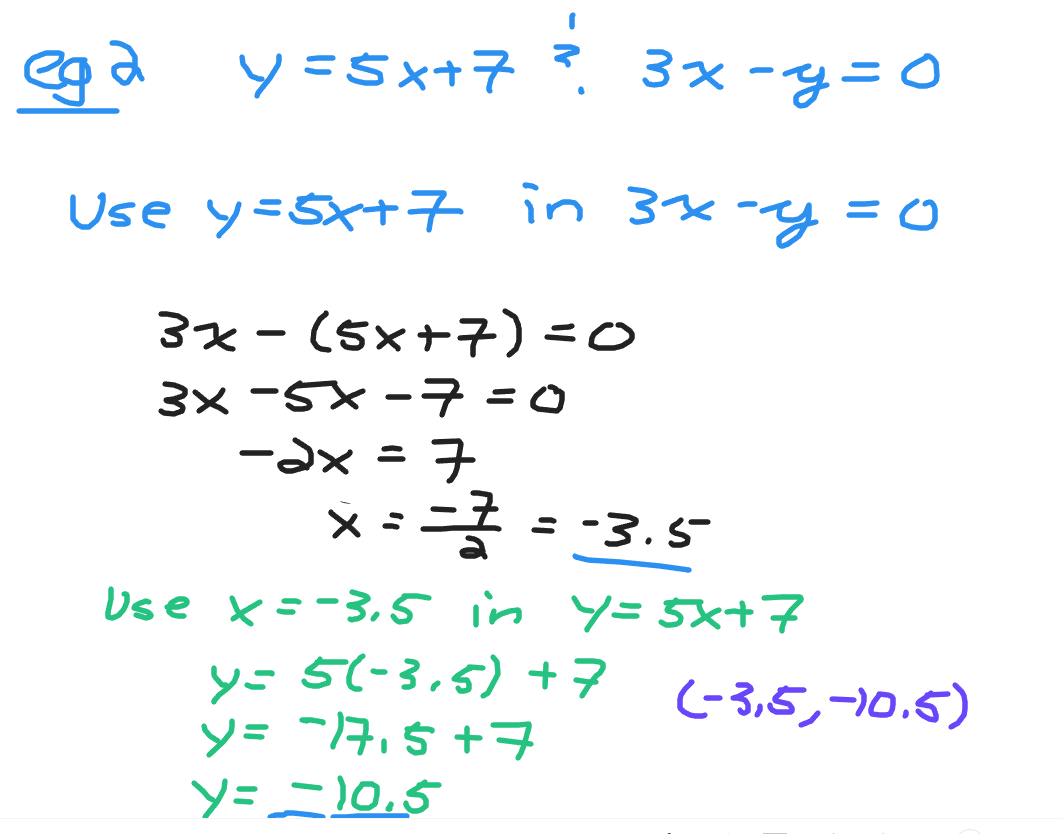
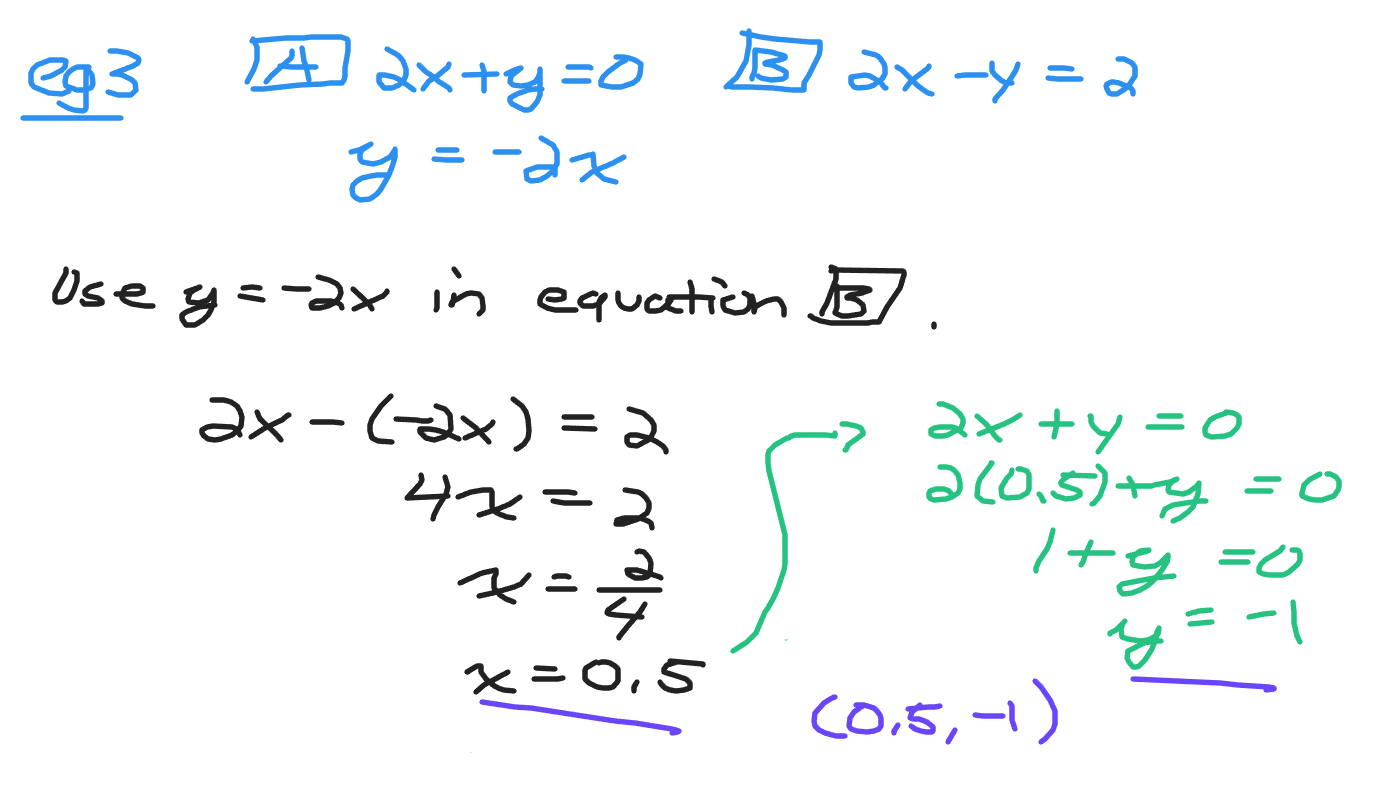

Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.