Determining Quadratic Functions From A Table Of Values
Hello and welcome. In this mathematics post, I cover the topic of determining quadratic functions given a table of values.
Math text is done with rendered Latex with QuickLatex.com.

What Is A Quadratic Function?
A quadratic function is a type of mathematical function of the form:

where x is the independent variable, f(x) is the dependent variable that depends on the value of x. The coefficients a, b and c are numeric values.
A linear function such as g(x) = 3x has g(x) being increased by 3 every time x is increased by 1. The increase is consistent and does not change every time x is increased by 1. With a quadratic function, every time x is increased by 1, the amount that f(x) increases by does not stay the same.
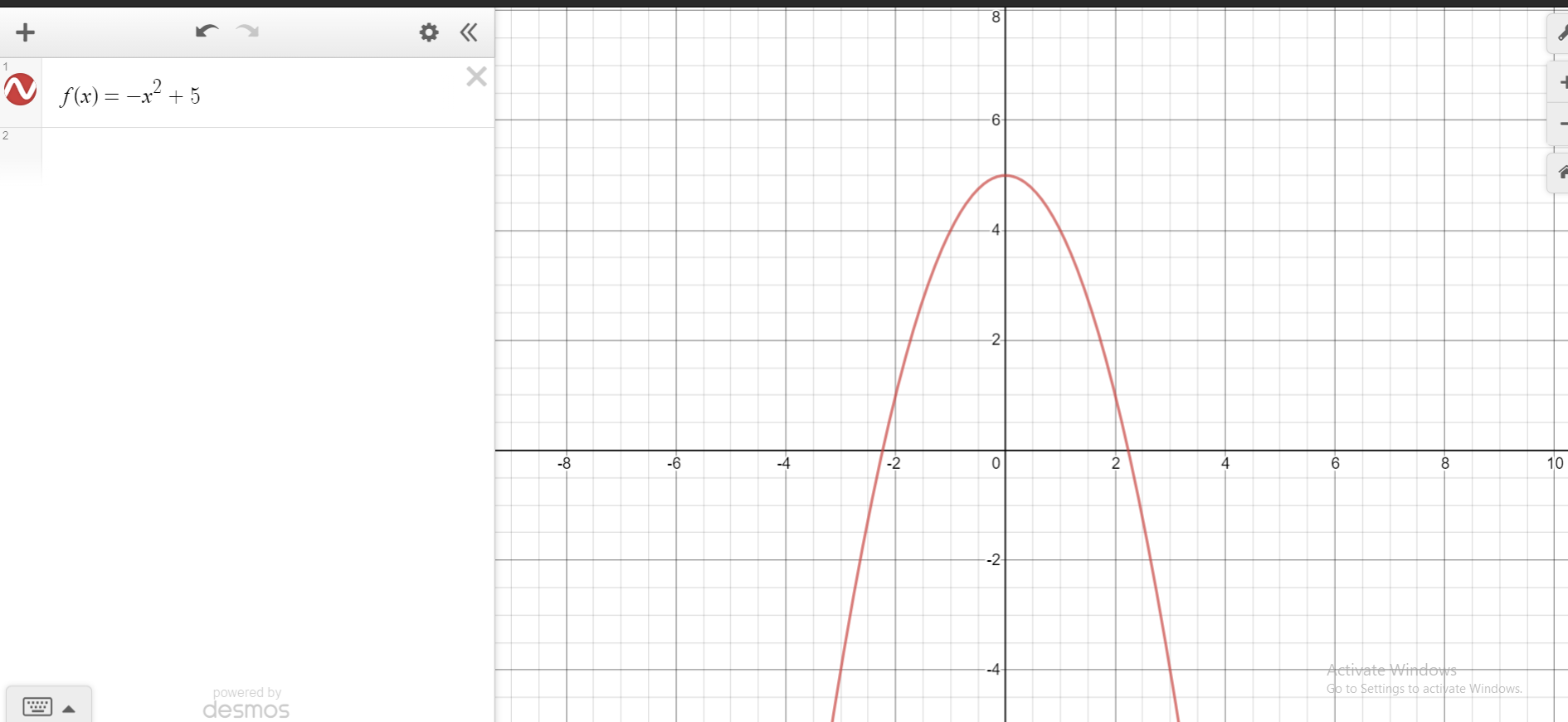
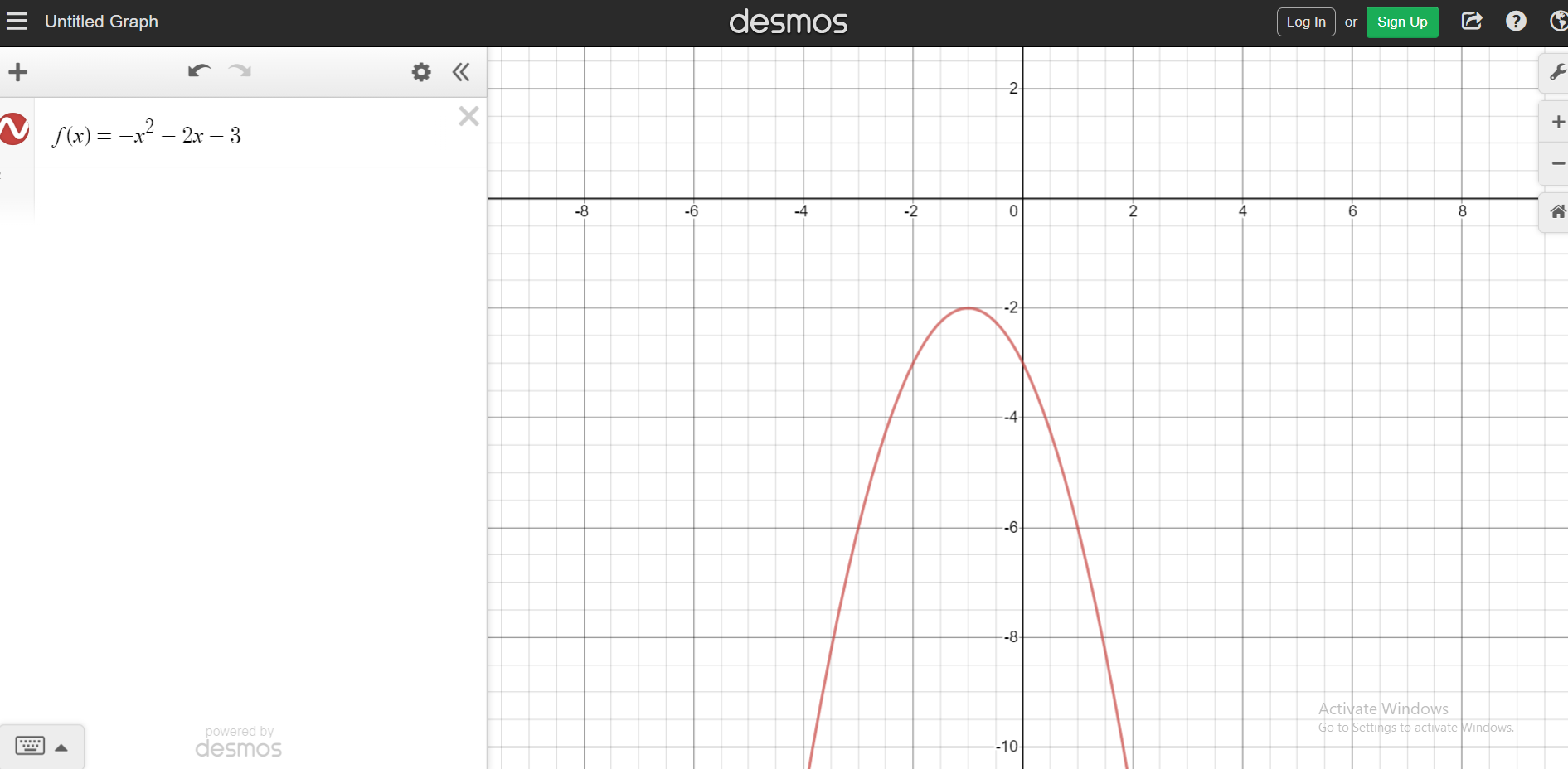
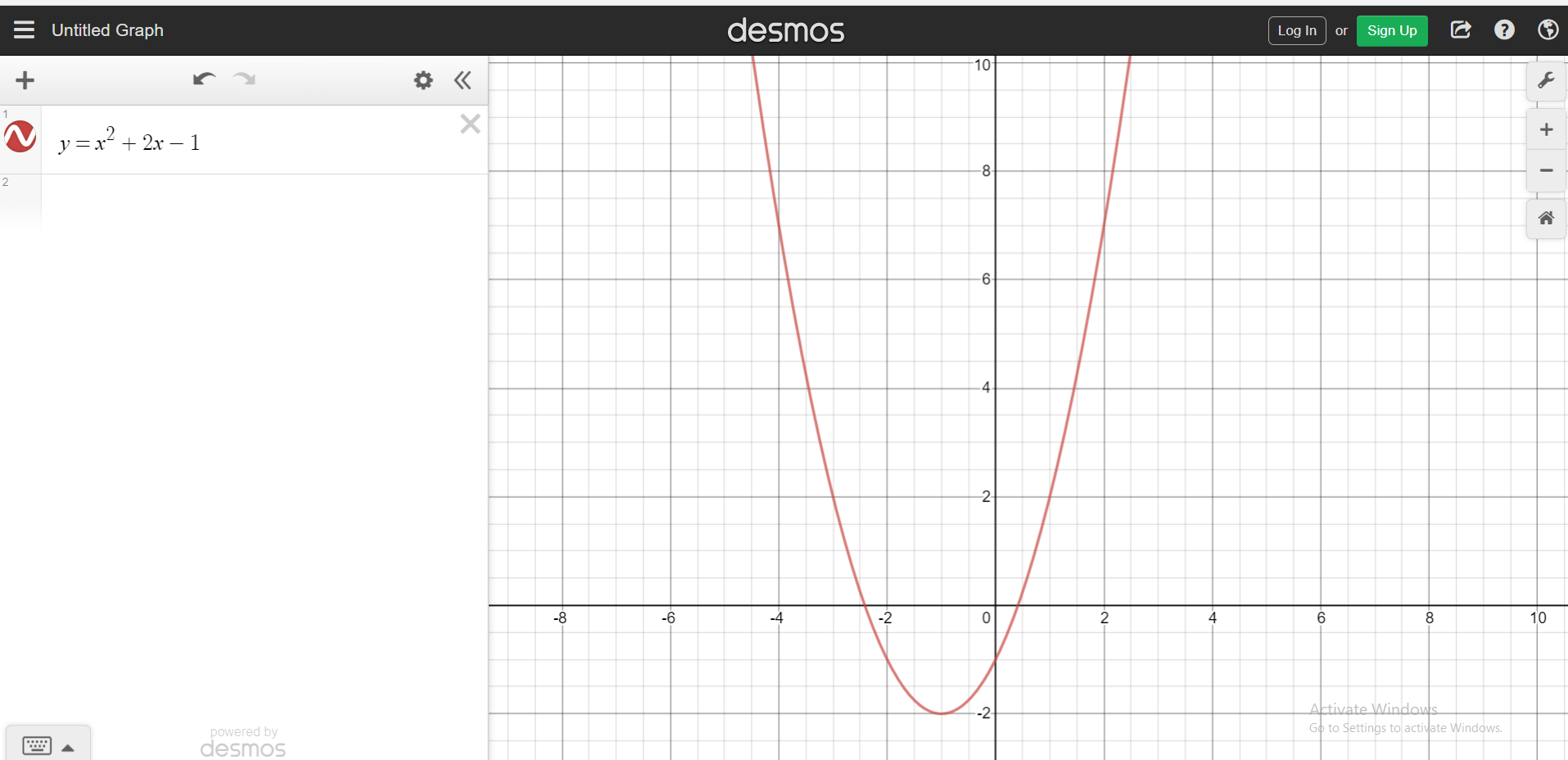
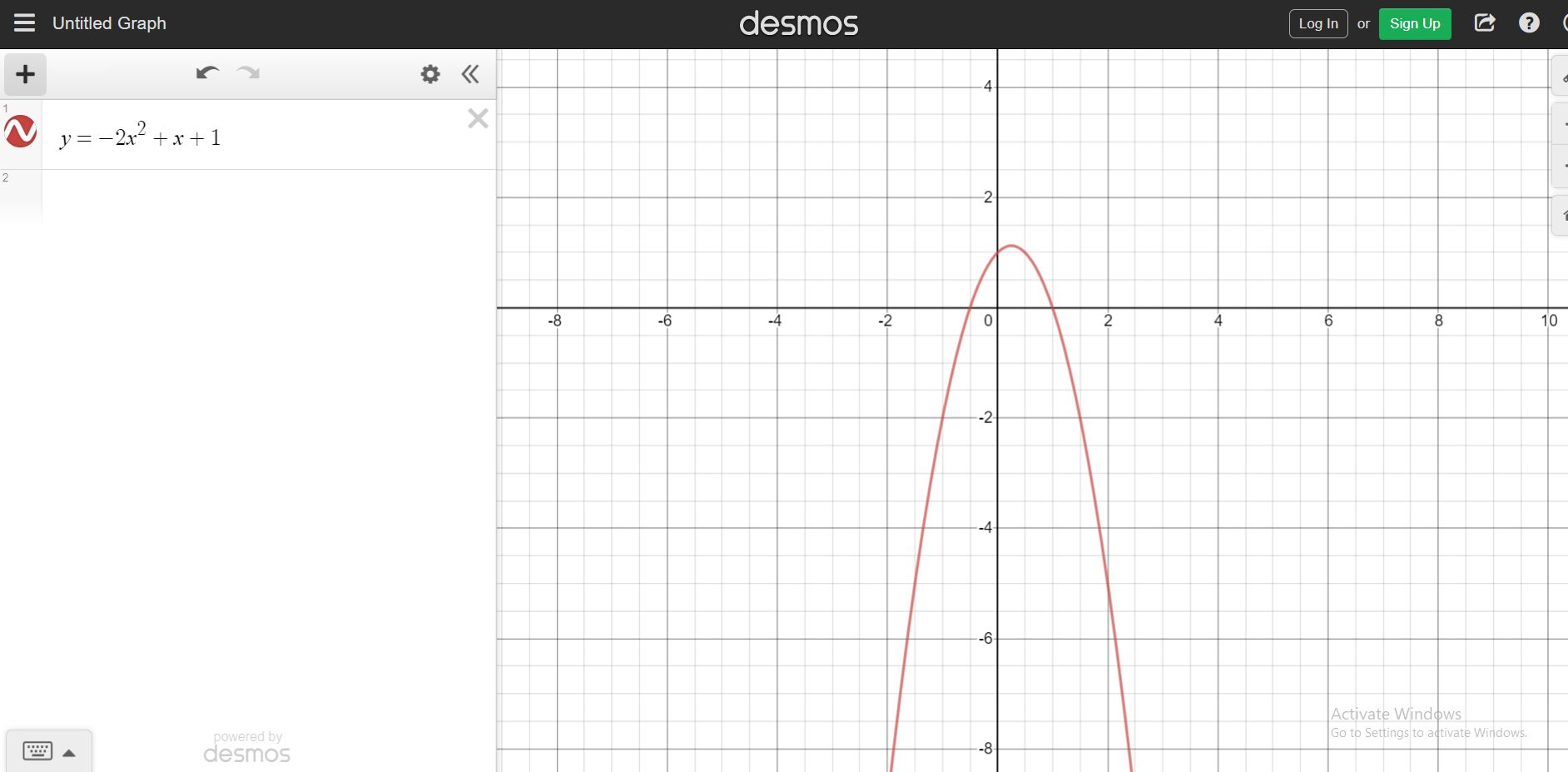
Examples Of Quadratic Functions
Let's take a look at some quadratic functions along with their graphs (Screenshots from Desmos). Different quadratic functions will their own shapes in how they open up and down.

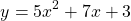
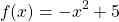

Using Table Of Values To Determine Quadratic Functions
There are times when all you have is just have a table of values. You need to determine if a quadratic function does fit the points from the table of values. If so, what is the quadratic function that does fit the points?
Example One
Here is a table of values for the quadratic function in this example.
| x | y |
|---|---|
| -2 | -1 |
| -1 | -2 |
| 0 | -1 |
| 1 | 2 |
| 2 | 7 |
| 3 | 14 |
We need to take a look at the first differences to see if there are the same. First differences takes a y-value minus the previous y-value if it exists.
| x | y | First Differences |
|---|---|---|
| -2 | -1 | N/A |
| -1 | -2 | -1 |
| 0 | -1 | +1 |
| 1 | 2 | +3 |
| 2 | 7 | +5 |
| 3 | 14 | +7 |
As the first differences are not the same throughout, the function that fits through these points is not a linear function. Let's take a look at the second differences.
| x | y | First Differences | Second Differences |
|---|---|---|---|
| -2 | -1 | N/A | N/A |
| -1 | -2 | -1 | N/A |
| 0 | -1 | +1 | +2 |
| 1 | 2 | +3 | +2 |
| 2 | 7 | +5 | +2 |
| 3 | 14 | +7 | +2 |
The second differences are the same which means that the function that fits these points is a quadratic function of the form 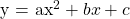 . What are the values for the coefficients though?
. What are the values for the coefficients though?
For the coefficient value of a, it is half of the second difference. In this example the value of a is half of 2 which is 1.
The value of c is the y-intercept. This is the value of y when the value of x is 0. For this example, the c value is -1.
Determining the value of b requires algebra along with substituting values from a point from the table in the quadratic function general form. I will use the point (1, 2).

The quadratic equation that fits the points in the table of values is  .
.
Example Two - Not A Quadratic Function
Not every table of values is associated with a quadratic function as shown in this example.
| x | f(x) |
|---|---|
| -2 | -6 |
| -1 | -3 |
| 0 | -2 |
| 1 | -3 |
| 2 | -7 |
Taking the first differences and the second differences gives this modified table.
| x | f(x) | First Differences | Second Differences |
|---|---|---|---|
| -2 | -6 | N/A | N/A |
| -1 | -3 | +3 | N/A |
| 0 | -2 | +1 | -2 |
| 1 | -3 | -1 | -2 |
| 2 | -7 | -4 | -3 |
The second differences are not the same. If you find one instance where the second difference is not the same in a table of values, then a quadratic function does not fit through all the points. There is no such quadratic function here.
Example Three
Notice how the last two examples include a y-intercept where there is a y-value when x is equal to 0. This example will show a case of a table of values where there is no y-intercept given.
| x | g(x) |
|---|---|
| 1 | 0 |
| 2 | -5 |
| 3 | -14 |
| 4 | -27 |
| 5 | -44 |
As x increases the amount for g(x) decreases. Let's take a look at the first differences and the second differences.
| x | g(x) | First Differences | Second Differences |
|---|---|---|---|
| 1 | 0 | N/A | N/A |
| 2 | -5 | -5 | N/A |
| 3 | -14 | -9 | -4 |
| 4 | -27 | -13 | -4 |
| 5 | -44 | -17 | -4 |
The second differences is a constant negative 4. The value for a in 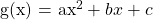 is half of -4 which is -2. We now need to determine the values for
is half of -4 which is -2. We now need to determine the values for b and c for the quadratic function that can fit through these five points. This has to be done with a system of equations.
Select two (x, y) points from the table and set up to equations. The first equation uses the x and y value pair from (1, 0) and the second equation uses the x and y pair from the point (2, -5).
First Equation
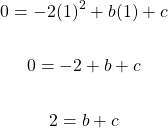
Second Equation
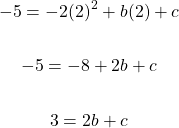
To solve this system of equations, you can use the elimination method, a substitution method, or even use matrices from linear algebra. For this example, I will use the substitution method as we can isolate the variable b (or c) in the first equation.
Start from the first equation:
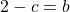
Use this value of b into the b in the second equation. Afterwards, solve for c.
In the second equation:
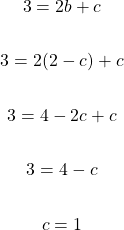
The value for c is found which can be used to find the value for b. I am using equation one to find b.
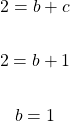
A lot has happened in this example. Here is a summary.
| x | g(x) | First Differences | Second Differences |
|---|---|---|---|
| 1 | 0 | N/A | N/A |
| 2 | -5 | -5 | N/A |
| 3 | -14 | -9 | -4 |
| 4 | -27 | -13 | -4 |
| 5 | -44 | -17 | -4 |
As the second difference is -4, this makes the value for a in the quadratic function half of -4 which is negative 2.
After some algebra, the quadratic function that fits through the (x, y) points above is 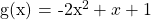 .
.
Posted with STEMGeeks
!discovery 35
This post was shared and voted inside the discord by the curators team of discovery-it
Join our community! hive-193212
Discovery-it is also a Witness, vote for us here
Delegate to us for passive income. Check our 80% fee-back Program