Determining Linear Functions
Hi. In this math post, I go over determining linear functions from a table of values.
Topics
- The Slope-Intercept Form Of A Line
- Common Difference Of Numbers As Slope
- Examples In Finding The Slope & Y-Intercept For The Equation Of A Line
The Slope-Intercept Form Of A Line
When you have two points, a line can be created that passes these two points. On the Cartesian plane a line has a slope and a y-intercept. When x = 0 the corresponding y-value with x = 0 is the y-intercept. The equation of the line is of the form:
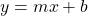
where m is the slope of the line and b is the y-intercept.

Common Difference Of Numbers As Slope
The slope of a line can be viewed as rise over run. This rise over run is the change in y-values divided by change in x-values.
From a table a values the slope is also the common difference.
Example
| x | y = x + 1 |
|---|---|
| -2 | -1 |
| -1 | 0 |
| 0 | 1 |
| 1 | 2 |
| 2 | 3 |
From the above example, the slope of the line is just 1. As x increases by 1, the value of y increases by 1 each time. The slope would be 1 divided by 1 which is just 1. This value of 1 is the slope which is also the difference in y-values as x increases by 1 each time.
Example Two
Determine the equation of the line from the following table.
| x | y |
|---|---|
| 0 | -2 |
| 1 | 1 |
| 2 | 4 |
| 3 | 7 |
| 4 | 10 |
From here the value of y goes up by 3 for each 1 unit increase of x. This value of 3 is the slope for the liine that passes the (x, y) points from the table of values.

Examples In Finding The Slope & Y-Intercept
There are cases where a y-intercept is not given from a table of values. Let's look at some examples.
Example One
| x | y |
|---|---|
| 2 | -3 |
| 4 | 0 |
| 6 | 3 |
| 8 | 6 |
In this table of values we do not have a y-intercept (y-value when x = 0). For every increase of x by 2 we increase y by 3. This is a slope of 3 divided by 2.
So far we have the equation of a line as:
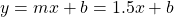
To find the y-intercept, we can use a (x, y) pair from the table of values to help solve for the y-intercept represented by b. I will use the point (4, 0) as my (x, y) point.
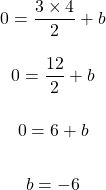
The equation of the line for the table of values in this example is y = 1.5x - 6.
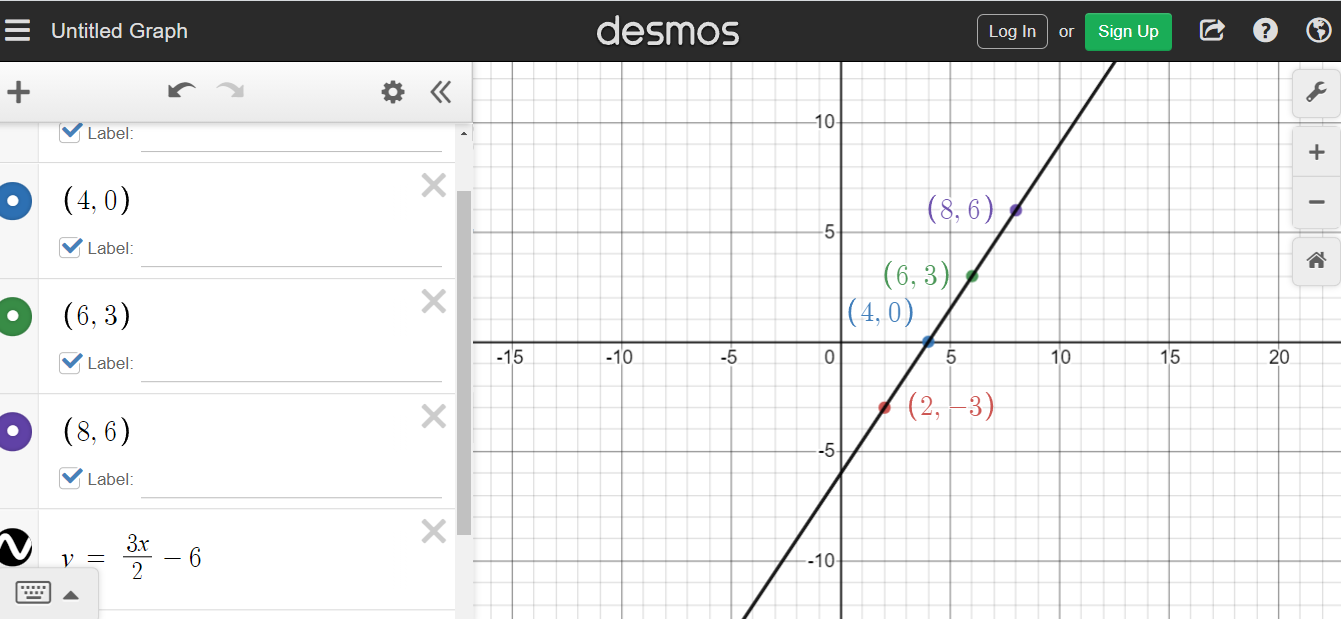
Example Two
| x | y |
|---|---|
| 1 | 8 |
| 4 | 2 |
| 5 | 0 |
| 10 | -10 |
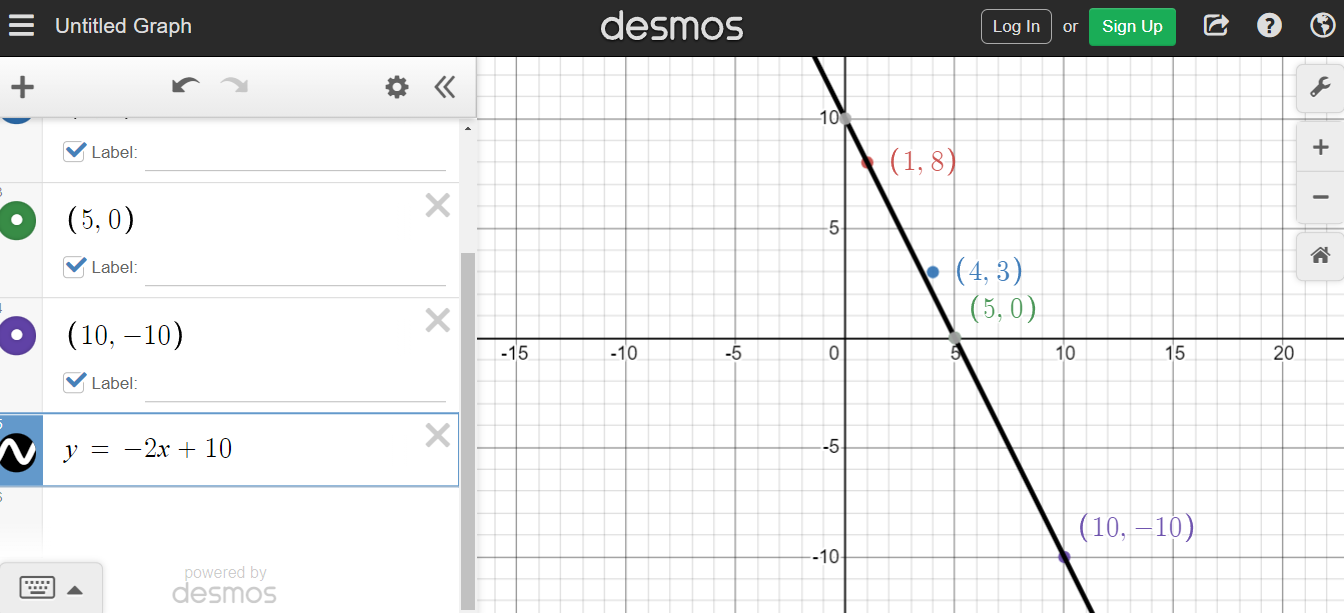
This table of values does not have equal spacing with the x-values. Do be mindful of this and check that the slope is the same between any two points here. For the purpose of this exercise I have made the table of values such that the slope is the same between any two points.
For computing the slope I use the points (4, 2) and (5, 0).
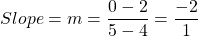
Now we solve for b in y = mx + b. The point (1, 8) is used for (x, y) to find b.
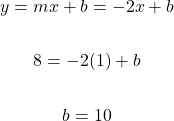
Example Three
I present here a more technical example. Look for how much y goes up by each time x increases by 1. Also the y-intercept is given.
| x | y |
|---|---|
| 0 | pi (π) |
| 1 | 3π |
| 2 | 5π |
| 3 | 7π |
| 4 | 9π |
From this table of values the y-intercept is pi π. When increases by 1, y increases by 2π. The slope here is 2π.
The equation of the line here is y = 2πx + π. Desmos screenshot below.
Posted with STEMGeeks

Electronic-terrorism, voice to skull and neuro monitoring on Hive and Steem. You can ignore this, but your going to wish you didnt soon. This is happening whether you believe it or not. https://ecency.com/fyrstikken/@fairandbalanced/i-am-the-only-motherfucker-on-the-internet-pointing-to-a-direct-source-for-voice-to-skull-electronic-terrorism
Electronic-terrorism, voice to skull and neuro monitoring on Hive and Steem. You can ignore this, but your going to wish you didnt soon. This is happening whether you believe it or not. https://ecency.com/fyrstikken/@fairandbalanced/i-am-the-only-motherfucker-on-the-internet-pointing-to-a-direct-source-for-voice-to-skull-electronic-terrorism
Electronic-terrorism, voice to skull and neuro monitoring on Hive and Steem. You can ignore this, but your going to wish you didnt soon. This is happening whether you believe it or not. https://ecency.com/fyrstikken/@fairandbalanced/i-am-the-only-motherfucker-on-the-internet-pointing-to-a-direct-source-for-voice-to-skull-electronic-terrorism
Fantastic calculation. I love the topic. Math is the simplest course if one understand the rudiments.
Yes, I do agree with this statement. There are cases where it takes to understand certain technical/abstract concepts. Getting over the hump can be tricky.