Determine Ratios - A Basic Math Guide
Hello. In this math guide I cover the topic of ratios. Ratios are used for comparing quantities of 2 or more different items.

Topics
- The Concept Of Ratios
- Equivalent Ratios & Equivalent Fractions
- Problem Solving With Ratios
The Concept Of Ratios
I am starting with an example. Three cups of flour to one cup of water is an example of a ratio. For every 3 cups of flour you have one cup of water. It is written as 3:1 for the cups of flour to water as a ratio.
You can also compare values in fraction form. Three to one in fraction form would be 3/1 where the top number or numerator is three and the bottom number or denominator is a 1.
Equivalent Ratios & Equivalent Fractions
In the previous section I have the example of 3 cups of flour for 1 cup of water. Another way to maintain this ratio is having 6 cups of flour to 2 cups of water. This is double the amount of the cups of flour and double the amount of the cups of water. This 6 cups of flour to 2 cups of water is an example of an equivalent ratio.
Equivalent ratios are also related to equivalent fractions. Ten kids with two teachers can be expressed in ratio form as 10:2 or in fraction form 10/2. This ratio of 10:2 can be reduced to 5:1 by taking half of 10 to obtain 5 and taking half of 2 to get the 1. This is 5 kids for 1 teacher. Screenshot picture shown below.
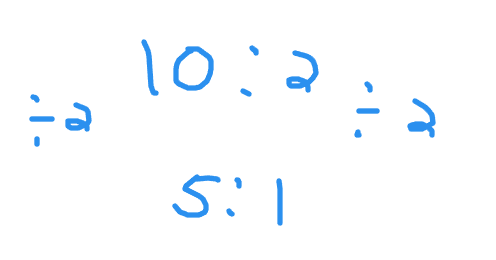
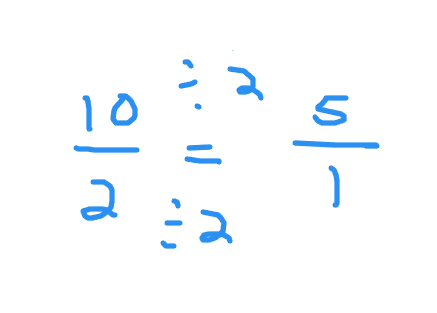
Problem Solving With Ratios
There are cases where you need to solve for missing numbers in equivalent ratios and in equivalent fractions. Here are some examples.
Example One
In a classroom there are 3 girls for every 2 boys. How many girls would there be if there are 12 boys in the classroom?
The ratio of girls to boys is 3:2. To get from 2 boys to 12 boys is multiplying by 6. This is because 2 times 6 gives 12. Six is not the answer but it is a helper number. We have six groups of 2 boys to get 12 boys. Apply this idea of 6 groups as in 6 groups of 3 girls to get the answer of 18 girls.
This question can be solved with the use of equivalent fractions too. Here is a screenshot image. The helper number of six is used.

Example Two
One bus carries 50 people. How many people can 8 buses carry?
As one bus carries 50 peoples you can have the ratio of 1:50 for the number of buses to people. Eight buses is eight times one. To obtain the answer multiply eight with fifty to get the number of people eight buses can carry. This answer is 400.
Example Three
I use the classroom setting again like in example one. There are 3 girls for every 2 boys. How many boys are there if there are 25 students of both boys and girls?
The ratio of girls to boys is 3:2. Include a total and the update the ratio as girls to boys to total. This updated ratio is 3 girls: 2 boys: 5 students.
The question asks for the number of boys if there are 25 students. This ratio is ?? girls: ?? boys: 25 students. We can obtain our helper number by comparing 5 students to 25 students. Five times something gives 25. This something or helper number is five.
Use this helper number of five and multiply it with 2 boys. The answer here is 10 boys in a class of 25 students when there are 3 girls for 2 boys.
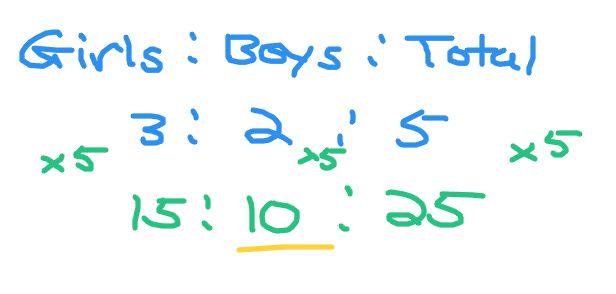
References

Posted with STEMGeeks
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.