Cross Multiplication
Hi there. In this math guide I would like to go over the concept of cross multiplication.
Reference: https://www.mathsisfun.com/algebra/cross-multiply.html

Topics
- The Cross Multiply Algebra Technique
- Why Cross Multiplication Works
- Solving For x With Cross Multiplication Examples
The Cross Multiply Algebra Technique
Suppose you are given two fractions that are equal to each other in this format:

where the values b and d are non-zero. (Cannot have division by zero.)
The cross multiplication technique converts the above equation into this:
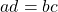
The d from the denominator of the right fraction goes with the a from the left fraction. The b from the denominator from the left fraction is multiplied with the c from the right fraction. I have included a visual below (From MathisFun website) as it is easier to see this concept versus reading text.

Example
Consider two equivalent fractions that are equal in value to each other.
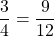
With cross multiplication, you would have this:
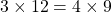
Both sides would equal 36.

Why Cross Multiplication Works
This section looks at why cross multiplication works. It does help to understand why something works instead of just using a technique without understanding.
Start with the equality of two fractions:

The goal is to remove the b and the d on the bottom of the fractions. This is done by multiplying both sides by b and multiplying both sides by d. The steps are shown below.
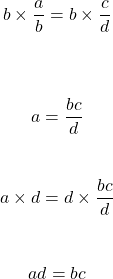

Solving For x With Cross Multiplication
Cross multiplication is a fast and easy tool that can really help with solving for x when there are fractions around. Here are some examples.
Example One
Solve for x in the following:
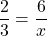
From cross multiplication, you have 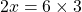 which is
which is 2x = 18. The value for x would be 9.
In this example, cross multiplication is not really needed. You can relate that 6 is three times 2 which makes the value of x being 3 times 3 which is 9.
Example Two
Solve for x in the following:
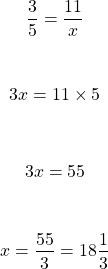
Example Three
What is the value of x?
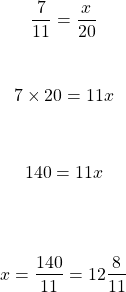
Example Four
The cost of 5 apples is 3 dollars. What would be the cost of 12 apples?
When it comes to setting up the fractions make sure that the apples numbers are both on the top or both on the bottom. The dollar amounts are also both on the top or bottom.
My setup here has the number of apples as the numerators of the fractions and the dollar amounts as the denominators of the fractions. You can do have the dollar amounts on the top with the number of apples on the bottom as a different setup.
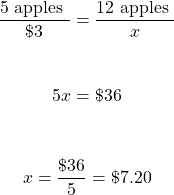
Assuming the same per unit price, the cost of 12 apples is $7.20.

Posted with STEMGeeks
Been a long time since I've seen how the actual math works. Good to know what is going on in my head when I come across an apple scenario like you described. :)
Great post, it's a very simple and easy explanation, I don't know why we collapsed in front of the math
That is good that you have found this guide easy to follow. I try to make it simple with a lot of my math guides and teaching at work.
Keep this up . This is what STEMGeeks or Hive needs . General topics which can bring traffic from outside.
Really amazing to see how we can explain why simple things works on Maths.