Arithmetic Sequences - A Guide
Hi there. In this guide, I cover the math topic of arithmetic sequences.
Topics
- Basic Number Patterns
- The Arithmetic Sequence
- Examples Of Solving For Missing Values In Arithmetic Sequences
Basic Number Patterns
Before getting into the definition of a arithmetic sequence I would like to share some basic number patterns. That is the number patterns you would have most likely seen as a kid or young student.
Count By 2
2, 4, 6, 8, 10, 12, ..., 100
Count By 10 Starting at 7
7, 17, 27, 37, 47, ..., 177
Subtract 5 Every Time
28, 23, 18, 13, 8, 3, -2, -7, -12, ..., -42
The Arithmetic Sequence
In a more mathematical setting the arithmetic sequence is based on these basic number patterns where the increase or decrease is the same in getting the next number. Here is a formula for obtaining any number in an arithmetic sequence.
t_n = t_1 + (n - 1)d

Note that the term t_1 is the first number in the sequence.
The term is t_n is the n-th term in the sequence. If n = 10 we have the tenth number or term in the arithmetic sequence.
The variable n is the number of terms in the arithmetic sequence.
The letter d represents how much the numbers go up or down in every step. A value of 2 for d would be counting up by 2 to get the next number as an example. A value of -10 for d would be subtracting 10 to get the next number.
Example One - Count By 8 Starting at 2
2, 10, 18, 26, 34, 42, 50, 58, 66
The first term here is two with a d value of eight. Fifty would be the seventh term in this sequence which you can represent as t_7 = 50.
As the number of terms in this sequence is 9 the value for n would be 9.
Example Two - Subtract By 10 Starting at 59
59, 49, 39, 29, 19, 9, -1, -11, -21, -31
With this arithmetic sequence we have:
- Ten values which would make
n = 10 - The first term as 59
- The final or tenth term as -31
- The common difference as negative ten
Examples Of Solving For Missing Values In Arithmetic Sequences
The arithmetic sequence formula can be used to find certain numbers in a sequence, the first number in the sequence, how many numbers are there in the sequence or the common difference.
Example One
The first number in the sequence is 2 with a common difference of 5. What is the twentieth number in this arithmetic sequence?
You could start at 2 and count by five until you get number/term 20. That could take a bit of time. The mathematical way of doing this would be using the arithmetic sequence formula.
Example Two - Find Number of Terms
Start with the number one and the last number in the arithmetic sequence as 232. The common difference is 11. How many terms are there in this sequence?
The first number or t_1 is 1 and let t_n = 232. Eleven would be the common difference as in d = 11. Use the arithmetic sequence formula, substitute the known values and solve for n.
Example Three - Determine Starting Number
An arithmetic sequence has a final number of -108 with a common difference of -8. There are 16 numbers in this sequence. What is the first number here?
Posted with STEMGeeks

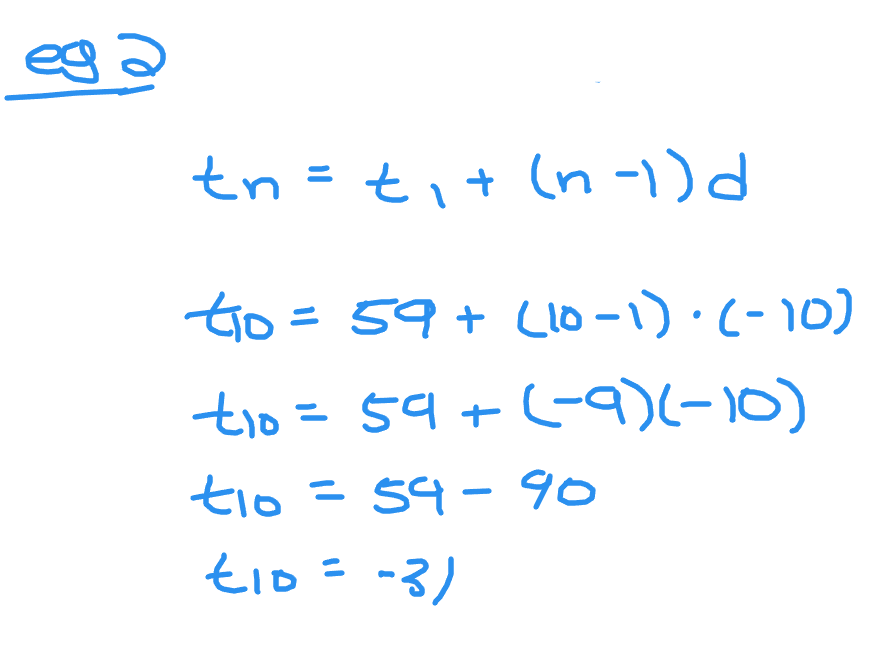
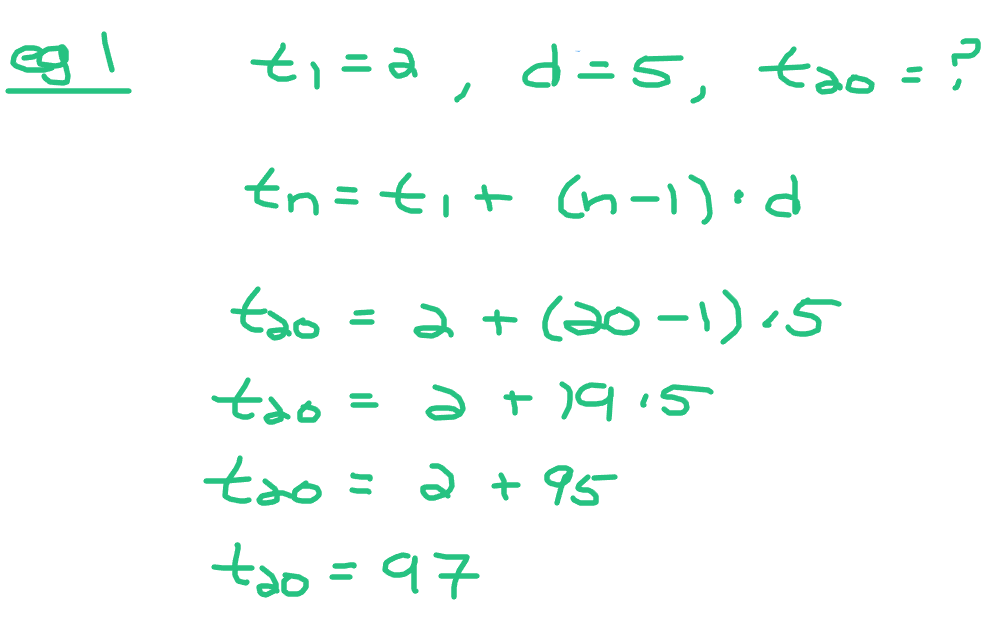

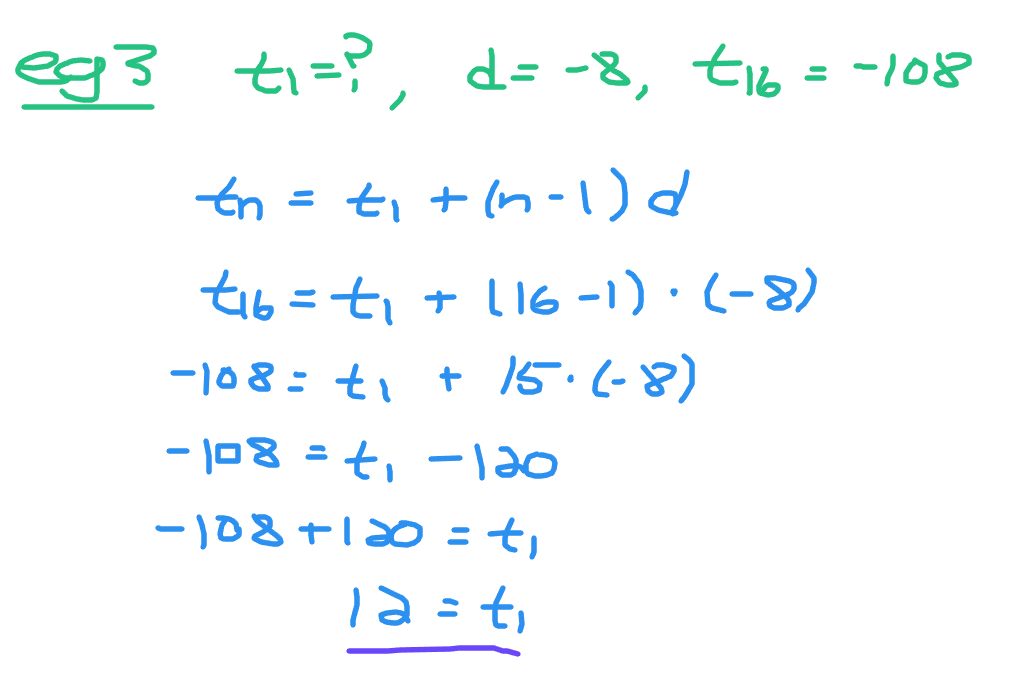
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.