Approximating Pi-Squared Over 6 With Python Programming

Hi there. In this math & Python post, I cover one way of approximating the value of pi in Python programming. It is based on this .pdf link here. That .pdf link mentions MATLAB but I'll use Python here.

This post is a bit technical with the mathematics.

Pictures are either from Quicklatex.com for math text or screenshots.

Pixabay Image Source

 

Topics

---

• For Loop As Sigma Sum Notation Or Product Notation
• Approximating Pi-Squared Divided By 6
• Approximating Pi

 

For Loop As Sigma Sum Notation Or Product Notation

---

You can relate the for loop from computer programming with the Sigma sum notation from mathematics. In mathematics, the sum notation is as follows:

 

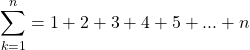
The for loop equivalent of the above in Python is something like:

total = 0

for k in range(1, n, 1):
  total = total + k

 

Instead of adding, there is also one for multiplying numbers to obtain a product. It is like this:

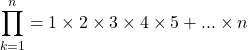
In Python, expression the product notation above would be something like:

product = 0

for k in range(1, n, 1):
  product = product * k

 

Approximating Pi-Squared Divided By 6

---

Here is the infinite series which is equal to pi-squared divided by 6.

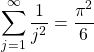
I create a function in Python that outputs the number of terms in the series given a maximum error (tolerance). This maximum error is based on the difference of the approximation to pi-squared over 6 and pi-squared over 6. A lower maximum error does give a better approximation but it does take longer. A balance between speed versus precision.

Error = Approximation - pi-squared over 6

Loop stops just when error is less than acceptable error (tolerance).

 

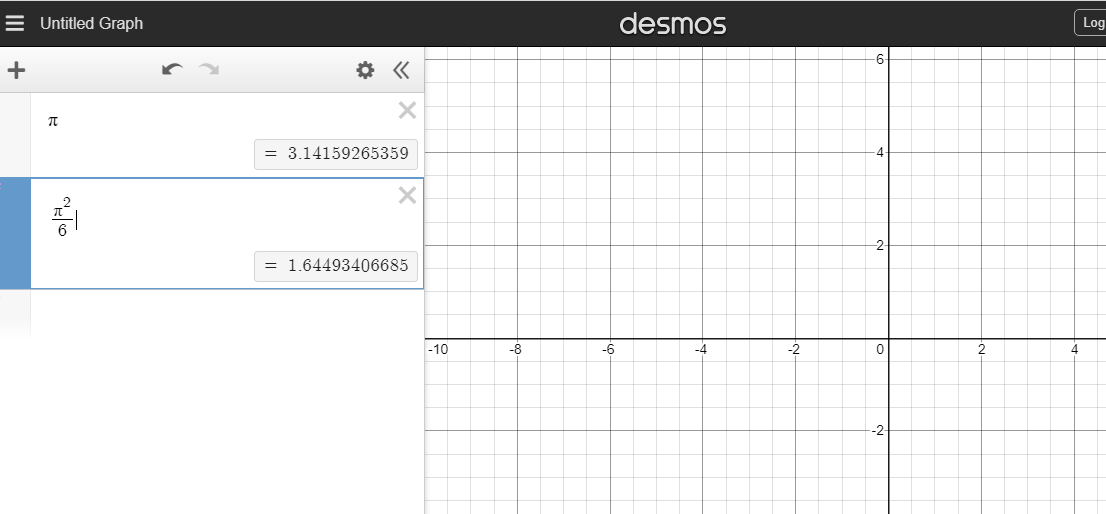
As a reference pi to 10 decimal places is about 3.1415926536. Pi-squared over 6 is about 1.64493 to 5 decimal places. (Screenshot from Desmos.)

Python Code

import math

# Approximate pi-squared over 6 given tolerance (acceptable error from approx to actual value)
# Number of terms given

def approx_pisq_tolerance(tolerance = 0.01):
    # Initialize total/sum, error, k (number of terms)
    total = 0
    error = 1
    k = 1
    # Keep looping until error is less than acceptable tolerance error:
    while error > tolerance:
        total += (k**(-2))
        error = abs(total - ((math.pi)**2 / 6))  
        k += 1
        
    print('Given a tolerance of ' + str(tolerance) + ' the number of terms needed is ' + str(k - 1) + '.')
    return(total, error)

 

In the function I have set the default tolerance error amount to be one hundredth. The user can change this if he or she wants to add more precision with the approximation to pi-squared over 6. Given a tolerance error, the function would output the number of terms needed in the series to obtain an error just less than the submitted tolerance error.

I first initalize the total/sum to zero and the error to 1. The error is set to 1 such that the while loop starts.

This while loop operates as long as the error is greater than the max error accepted. In each loop in the while loop I obtain the value that corresponds to k and add that to the running total/sum. Then I increment k by 1 just like with sum notation.

Note that in the print statement I use k-1 as the k-1 term is not evaluated.

 

Function Call

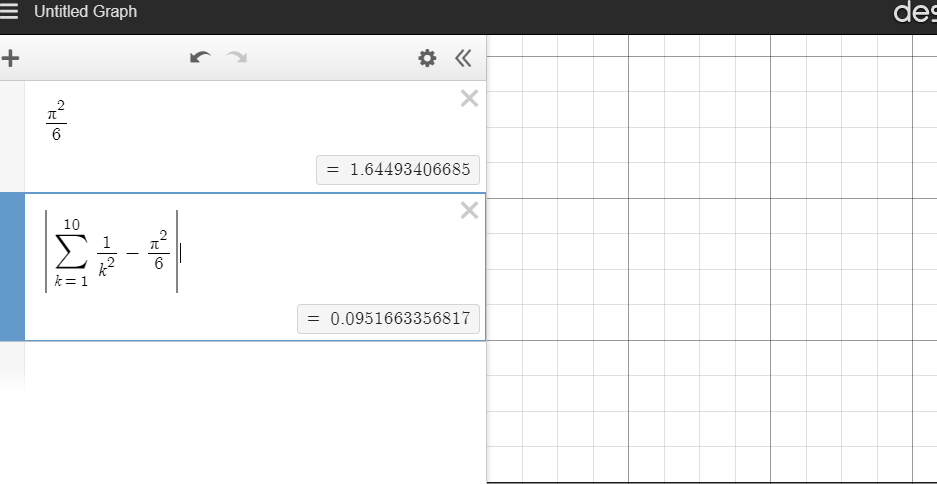
Doing a function call of tolerance of 0.1 gives this output. Screenshot from my jupyterNotebook and Desmos screenshot to verify.

 

Approximating Just Pi

---

With rearrangement of the formula and code adjustments, the value of pi can be approximated in Python.

 

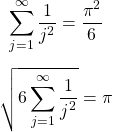
Python Code

def approx_pi_tolerance(tolerance = 0.01):
    # Initialize total/sum, error, k (number of terms)
    total = 0
    error = 1
    k = 1
    # Keep looping until error is less than acceptable tolerance error:
    while error > tolerance:
        total += 6 * (k**(-2))
        error = abs(math.sqrt(total) - math.pi)  
        k += 1
        
    print('Given a tolerance of ' + str(tolerance) + ' the number of terms needed is ' + str(k - 1) + '.')
    return(math.sqrt(total), error)

 

The code is not much different in terms of format compared to approximating pi-squared over 6. In this code, it is important to take the square root when computing the error.

Function Calls

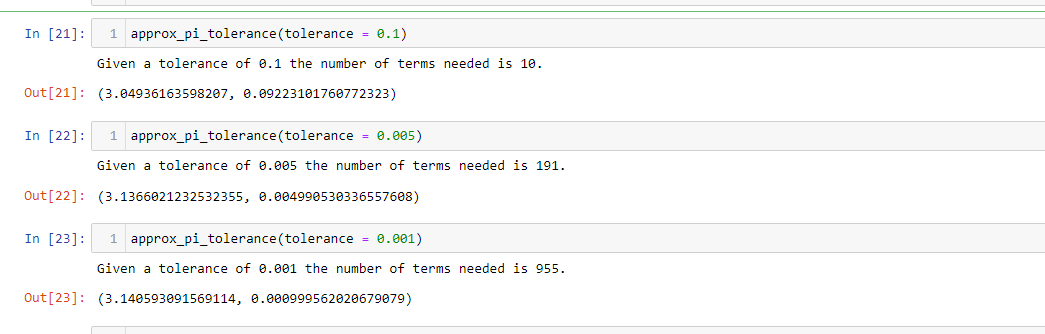
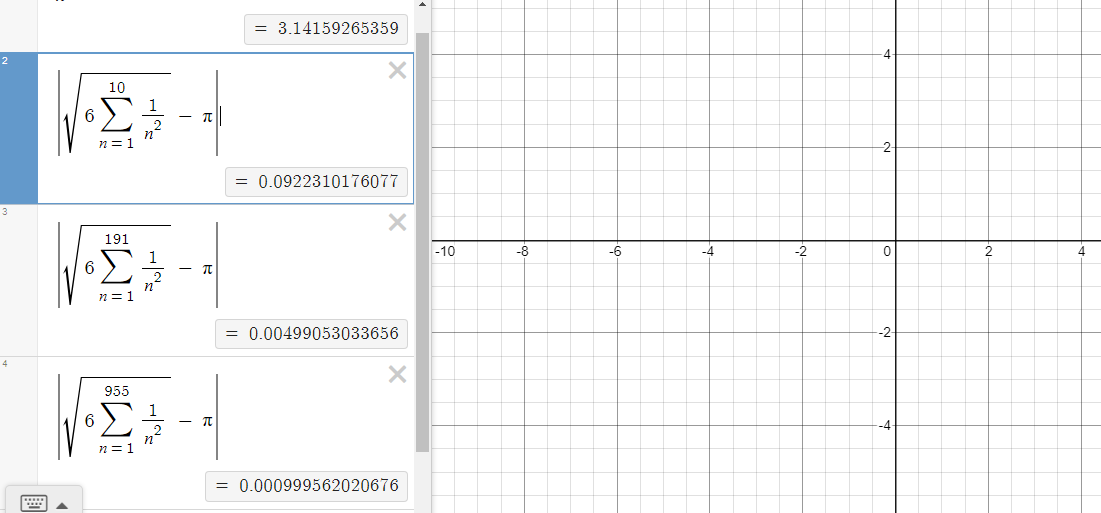
Here are the function calls along with a Desmos screenshot as a check.

 

Thank you for reading.

Posted with STEMGeeks