Acoustic applications - Les applications acoustiques

In my previous posts, I shared :
- My first thesis ever
- The history of the acoustic snitch !.
- The acoustic snitch [The definitions]
- The Physical Study of sound - L'Étude Physique du son
In this post, I would like to share ''Acoustic applications'' !
I'll translate it from French to English !

Acoustic applications :
Doppler effect :
As seen previously, a sound wave coming from a stationary point source is represented in the plane by a set of concentric circles. In case, where the source does not move, wherever you are, relative to the sound source, you will hear a sound of the same height. The frequency ( f ) is constant around the source.
If now we have to do with a mobile source, here is the representation :
Les applications acoustiques :
Effet Doppler :
Comme vu précédemment, une onde sonore provenant d'une source ponctuelle immobile se représente dans le plan par un ensemble de cercles concentriques. Dans le cas, où la source ne bouge pas, où que vous soyez, par rapport à la source sonore, vous entendrez un son de même hauteur. La fréquence ( f ) est constante autour de la source.
Si maintenant, nous avons à faire à une source mobile, en voici la représentation.
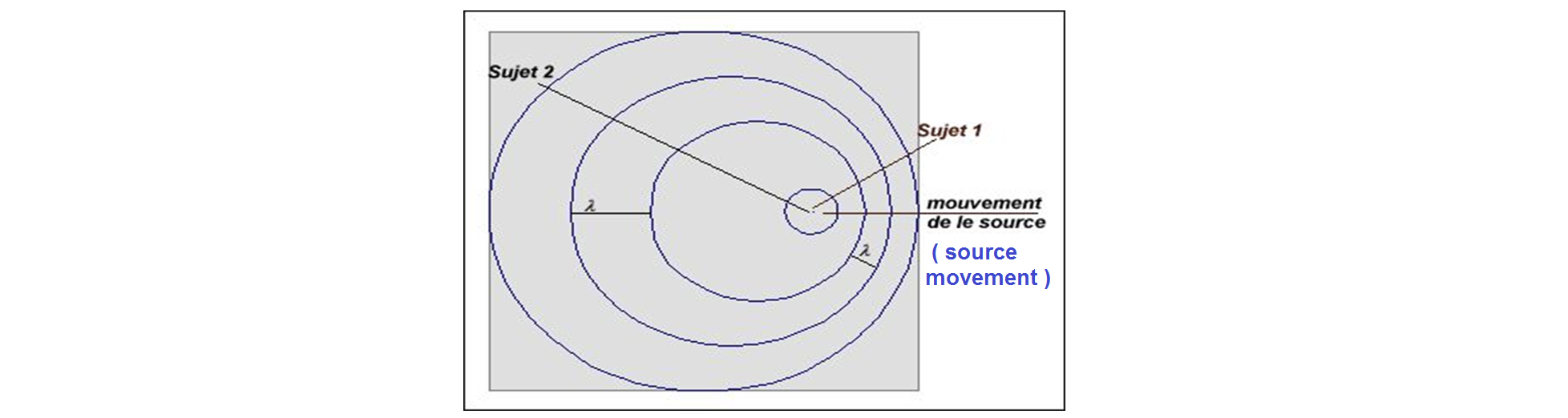
We find that the wavelength (L) varies depending on where the observer is. Or V = L x F
And we know that V is constant if there is no change of medium or temperature. (In air at 15 ° C, V = 340 m / s). Since V is constant and L varies, F also varies. When L decreases, F increases and when L increases, F decreases. L and F are therefore inversely proportional.
On the graph, subject 1 hears a higher sound than subject 2 because the frequency of the sound that subject 1 hears is greater than that of the sound audible by subject 2. This phenomenon is encountered whenever the distance between the source and observer varies.
Nous constatons que la longueur d'onde ( L )varie selon l'endroit où l'observateur se trouve. Or V = L x F
Et nous savons que V est constante s'il n'y a pas de changement de milieu ou de température. (Dans l'air à 15°C, V = 340 m/s). Comme V est constante et que L varie, F varie aussi. Quand L diminue, F augmente et quand L augmente, F diminue. L et F sont donc inversement proportionnels.
Sur le graphe, le sujet 1 entend un son plus aigu que le sujet 2 car la fréquence du son que le sujet 1 entend est plus grande que celle du son audible par le sujet 2. On rencontre ce phénomène chaque fois que la distance entre la source et l'observateur varie.
It was the Austrian mathematician, physicist and astronomer J. C. Doppler who first enunciated, in 1842, the laws expressing the variation in the pitch of a sound perceived as a function of the speed of the source relative to the observer. We can now understand why when a fire truck approaches us we hear its high alarm and when it pulls away the sound becomes lower.
It is thanks to this Doppler effect that police radars can determine the speed of a vehicle. Indeed, they will send an electromagnetic wave on the moving vehicle and will analyze the frequency of the reflected wave, by calculations they will be able to determine the speed of this vehicle.
C'est le mathématicien, physicien et astronome autrichien J. C. Doppler qui énonça le premier, en 1842, les lois exprimant la variation de la hauteur d'un son perçu en fonction de la vitesse de la source par rapport à l'observateur.
Nous pouvons maintenant comprendre pourquoi quand un camion pompier s'approche de nous, nous entendons son alarme aiguë et quand il s'éloigne, le son devient plus grave.
C'est grâce à cet effet Doppler que les radars des policiers peuvent définir la vitesse d'un véhicule. En effet, ils vont envoyer une onde électromagnétique sur le véhicule en mouvement et vont analyser la fréquence de l'onde réfléchie, par calculs ils pourront déterminer la vitesse de ce véhicule.
The sound barrier :
We have all heard the "bang" caused by an airplane going through the sound barrier. Nowadays, we don't hear it anymore because it is forbidden for planes to pass the sound barrier anywhere. Let's explain how this bang is produced.
When a plane flies, it produces a sound wave, this one propagates at an approximate speed of 294.444 m/s (1060km/h) and not of 340m/s as seen previously because where the planes fly, the temperature n is not 20 ° C and the pressure is lower.
Le mur du son :
Nous avons déjà tous entendu le "bang" causé par un avion qui passe le mur du son. De nos jours, nous ne l'entendons plus car il est interdit aux avions de passer le mur du son n'importe où. Expliquons comment ce bang est produit.
Lorsqu'un avion vole, il produit une onde sonore, celle-ci se propage à une vitesse approximative de 294.444 m/s (1060km/h) et non de 340m/s comme vu précédemment car là où vole les avions, la température n'est pas de 20°C et la pression est plus faible.

The first image represents the sound waves produced by an airplane flying at a speed of less than 1060 km / h. In this case we hear the plane before it has passed.
On the second image, an airplane flying at the speed of sound is represented, a shock wave is formed in the front of the airplane.
In picture three, the plane has passed the sound barrier, it flies at over 1060 km/h and when we hear the plane, it is already very far. As it passes the sound barrier, it crosses the shock wave and produces a "bang" which will propagate to the ground like a cone.
La première image représente les ondes sonores produites par un avion volant à une vitesse inférieure à 1060 km/h. Dans ce cas nous entendons l'avion avant qu'il ne soit passé.
Sur la deuxième image, est représenté un avion volant à la vitesse du son, il se forme une onde de choc à l'avant de l'avion.
Sur l'image trois, l'avion a passé le mur du son, il vole à plus de 1060 km/h et quand nous entendons l'avion, il est déjà bien loin. Au moment où il passe le mur du son, il traverse l'onde de choc et produit un "bang" qui va se propager jusqu'au sol à la manière d'un cône.
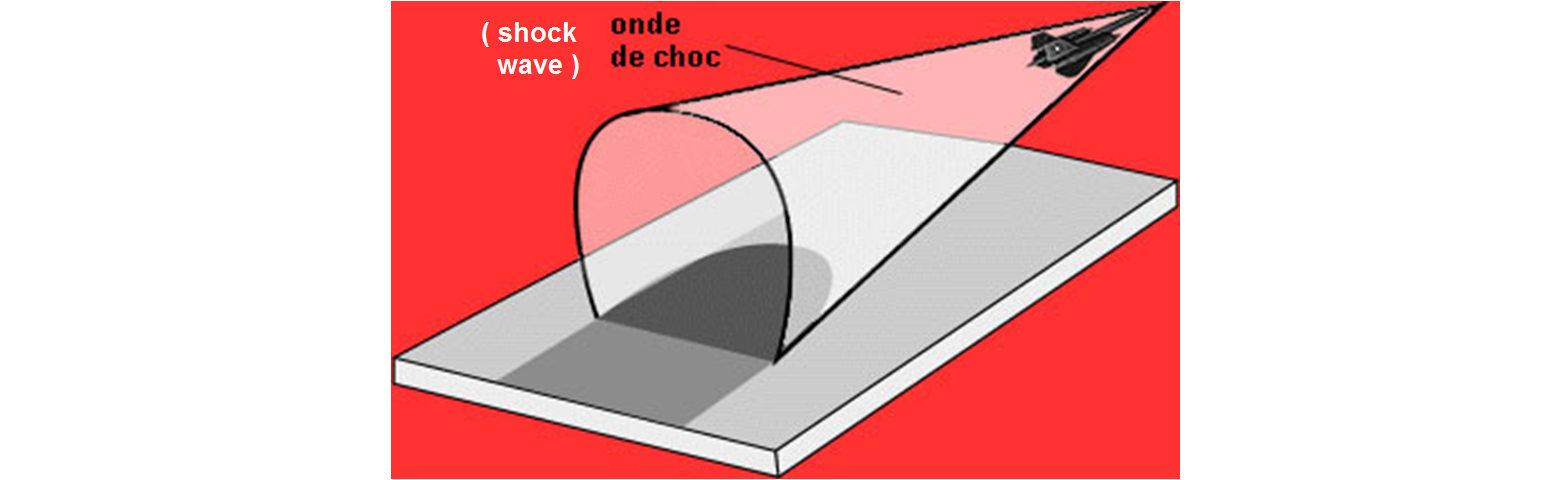
Figure: Imaginary representation of the shock wave.
How many kilometers away does lightning fall :
Since our early childhood, we can easily calculate the distance between us and lightning. We just have to count the seconds between the lightning and the noise made by the lightning, divide the number obtained by three, and we have this distance expressed in kms. This way of calculating is not precise, but is based on an interesting principle.
A combien de kilomètres tombe la foudre ?
Depuis notre tendre enfance, nous pouvons aisément calculer la distance qui nous sépare de la foudre. Il nous suffit de compter les secondes entre l'éclair et le bruit que fait la foudre, diviser le nombre obtenu par trois et nous avons cette distance exprimée en kms. Cette façon de calculer n'est pas précise mais repose sur un principe intéressant.
First, what is lightning? It's actually an electric arc, a big spark, a transfer of electrons through a mass of air. This spark makes a noise because it heats the air it passes through and expands it, causing a sound wave (pressure wave). The sound and the light of the lightning are produced at the same time, but if we perceive the lightning before hearing the thunder, it is because the light and the sound do not propagate at the same speed. Light travels at a speed of 3 x 108 m/s, which is equivalent to 1,080,000,000 km/h while sound travels only at a speed of 340 m/s (in air at 15 ° C), which is equal to 1224 km/h. Considering the high speed of light, we can consider that the time between when the lightning is produced and when we see it is zero. The sound takes 2.94 s to travel 1 km, as this time is variable depending on the air temperature and for the sake of ease, we generally round it down to 3 s. If the lightning falls at 6 km, we will therefore count 6 x 3 = 18 s. And here is our little checked childhood game.
Tout d'abord, qu'est-ce que la foudre ? C'est en fait un arc électrique, une grosse étincelle, un transfert d'électrons à travers une masse d'air. Cette étincelle produit un bruit car elle échauffe l'air qu'elle traverse et le dilate, ce qui provoque une onde sonore (onde de pression). Le son et la lumière de la foudre sont produits en même temps mais si nous percevons l'éclair avant d'entendre le tonnerre c'est parce que la lumière et le son ne se propagent pas à la même vitesse. La lumière se propage à une vitesse de 3 x 108 m/s, ce qui équivaut à 1 080 000 000 km/h alors que le son ne se propage qu'à la vitesse de 340 m/s (dans l'air à 15°C), ce qui est égal à 1224 km/h. Vu la vitesse élevée de la lumière, nous pouvons considérer que le temps entre le moment où l'éclair est produit et celui où nous le voyons est nul. Le son lui, prend 2,94 s pour parcourir 1 km, comme ce temps est variable en fonction de la température de l'air et par souci de facilité, nous l'arrondissons en général à 3 s. Si la foudre tombe à 6 km, nous compterons donc 6 x 3 = 18 s. Et voici notre petit jeu d'enfance vérifié.
Echoes and interference :
Sometimes unwanted echoes can occur in rooms with adequate reverberation time and built according to the rules set out above. These echoes are usually due to the concavity of a highly reflective wall or ceiling. As the sound is then concentrated at a given point, the acoustics are therefore very poor. Likewise, a narrow corridor made up of two reflecting walls can trap sound waves by successive reflections, and thus generate disturbing echoes, even if the overall absorption of the corridor is satisfactory.
Il arrive que des échos indésirables se produisent dans des salles pourvues pourtant d’un temps de réverbération convenable, et construites selon les règles établies ci-dessus. Ces échos sont généralement dus à la concavité d’un mur ou d’un plafond hautement réfléchissants. En effet, le son se trouvant alors concentré en un point donné, l’acoustique s’y avère par conséquent très mauvaise. De la même manière, un étroit corridor composé de deux murs réfléchissants peut piéger les ondes sonores par réflexions successives, et engendrer ainsi des échos perturbateurs, même si l’absorption globale du corridor est satisfaisante.
Besides echoes, the elimination of interference also deserves special attention. Such interference occurs between incident and reflected sound waves, creating areas called points of silence, in which certain frequencies have disappeared and canceled out. Reproducing sounds recorded by a microphone also requires elimination of echoes and interference.
Outre les échos, l’élimination des interférences mérite également une attention particulière. De telles interférences se produisent entre les ondes sonores incidentes et réfléchies, engendrant des zones appelées points de silence, dans lesquelles certaines fréquences ont disparu en s’annulant. La reproduction de sons enregistrés par un microphone nécessite également l’élimination des échos et des interférences.
Echo phenomenon :
When acoustic waves are reflected off an obstacle, they return a sound which results in an echo. The perceptible time interval between sound emission and repetition represents the time it takes for sound waves to travel back and forth. An echo is often weaker than the original sound, because only part of the waves are reflected.
Lorsque des ondes acoustiques se réfléchissent sur un obstacle, elles renvoient un son qui se traduit par un écho. L'intervalle de temps perceptible entre l'émission et la répétition du son représente le temps nécessaire aux ondes sonores pour parcourir l'aller-retour. Un écho est souvent plus faible que le son de départ, car seule une partie des ondes se trouve réfléchie.
That was the first chapitre of my first thesis !
In my next posts I'll share the second one.
It's really fun to learn about sound. ☺
Posted with STEMGeeks