Una historia imaginaria pero real, aunque parezca absurda - 2da Parte

La imagen de fondo de la portada es una imagen de libre uso tomada de Unsplash y editada por @abdulmath con GIMP, los emoji son creados con Bitmoji
Continuando con la historia imaginaria pero real, mientras por un lado Herón casi seguramente tenía que estar al tanto de la aparición de la raíz cuadrada de un número negativo en el problema del frustum, su colega alejandrino de dos siglos más tarde, Diofanto, parece haber pasado completamente por alto un acontecimiento similar cuando se tropezó con él.
Actualmente, se considera a Diofanto como que desempeñó en el álgebra el mismo papel que Euclides en la geometría. Euclides nos proporcionó sus Elementos, y Diofanto presentó a la posteridad la Aritmética. En ambos casos, la información contenida era casi con toda seguridad los resultados de muchos matemáticos anteriores y anónimos cuyas identidades se han perdido para siempre en la historia.
Sin embargo, fueron Euclides y Diofanto quienes recogieron y organizaron este patrimonio matemático de forma coherente en sus grandes obras.

Es muy importante notar que cada problema de Arithmetica es único en sí mismo, como los del Papiro Matemático de Moscú. Pero esto no quiere decir que las soluciones dadas no sean ingeniosas, y en muchos casos incluso diabólicamente inteligentes. La Arithmetica sigue siendo un excelente territorio de búsqueda para los profesores de álgebra de bachillerato que desee encontrar problemas que desafíen, e incluso dejen perplejos, a los estudiantes más brillantes.
Uno de esos problemas que mencionamos, lo encontramos en el libro 6, especificamente el número 22, el cual se enuncia de la siguiente manera:
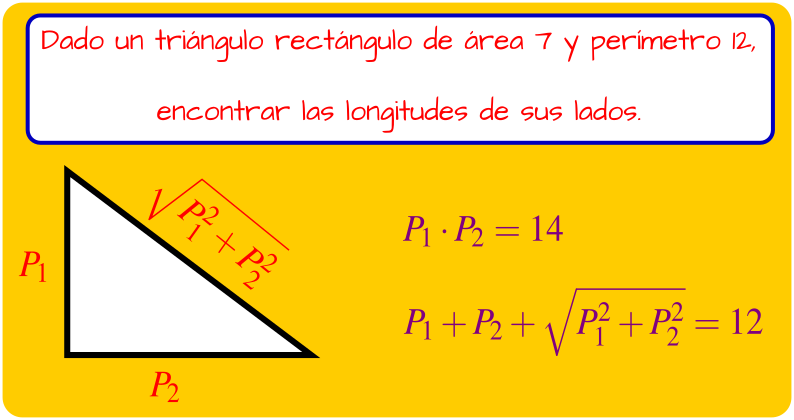

Ahora bien, este sistema de ecuaciones, se podría resolver usando una adecuada manipulación algebraica rutinaria, aunque la misma podría llegar a ser algo larga, pero la brillante idea de Diofanto fue la de reducir inmediatamente el número de variables del sistema de dos a una variables, escribiendo P1 = 1/x y P2 = 14x.
Entonces la primera ecuación se reduce a la identidad 14 = 14, y la segunda a:
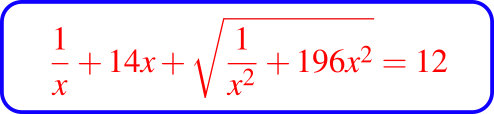
la cuál luego de manipulación algebraica es sencillo reducirla a la ecuación
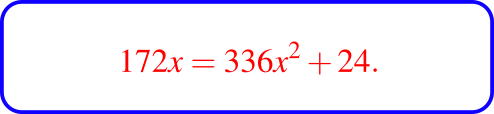
A modo de un ejercicio bastante útil e ilustrativo sería intentar resolver directamente las ecuaciones originales con las variables P1 y P2, y luego mostrar que los resultados son consistentes con la solución planteada por Diofanto.

De hecho, en otra parte de la Arithmetica, especificamente en el libro 5, el problema 2 escribió, que la ecuación 4x + 20 = 4, que era absurda porque conduciría a la solución imposible x = - 4. De acuerdo con esta posición, Diofanto utilizaba sólo la raíz positiva cuando resolvía una cuadrática. Ya en el siglo XVI encontramos matemáticos que se refieren a las raíces negativas de una ecuación como ficticias o absurdas o falsas.

Imagen de Pixabay y editada por @abdulmath con GIMP, el emoji es creado con Bitmoji.
Si quedastes fascinado con este apasionante tema de la historia de la matemática, no te pierdas la próxima publicación, si deseas ampliar más te invito a leer las siguientes referencias:
- W. W. Beman, A Chapter in the History of Mathematics, Proceedings of the American Association for the Advancement of Science 46 (1897):33–50.
- Richard J. Gillings, Mathematics in the Time of the Pharaohs, MIT Press 1972.
- E. T. Bell, The Development of Mathematics, McGraw-Hill 1945.


