30-11-2024- Analytic Geometry - Polarity [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH
30-11-2024- Analytic Geometry - Polarity [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_56)

Polarity

Description
In analytical geometry, polarity is a geometric relation between points and lines defined with respect to a conic (for example, an ellipse, a hyperbola or a parabola). It is a concept related to the theory of conics and projective properties.

Definition
Data:
-A conic C
For example described by the following general equation

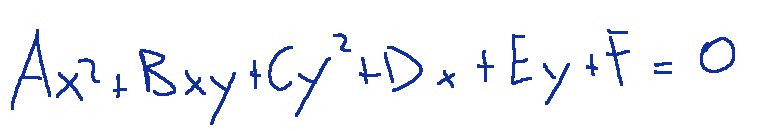
-A point P (x0,y0) that does not belong to the conic
A polar line called polar P is associated with the point P with respect to the conic C. Similarly, the point P is called the pole of the associated line.

Another definition
Let C be a non-degenerate conic with associated matrix A. Given a point

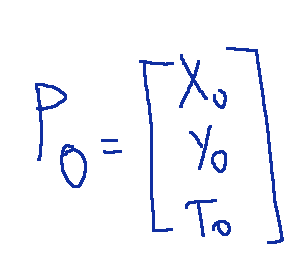
of the projective plane, the polar line or, simply, polar of P0 with respect to the conic C is the line with the implicit form homogeneous

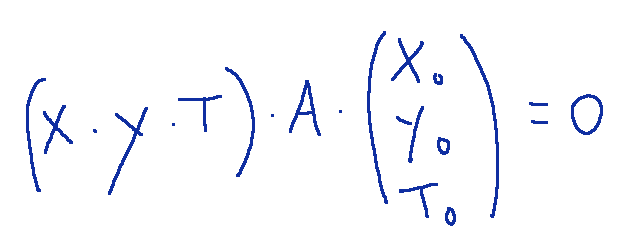
or

where

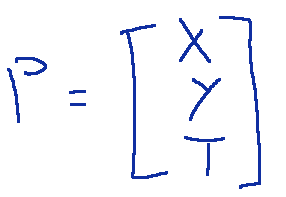
Example
Let's try to consider the ellipse C with the following homogeneous equation

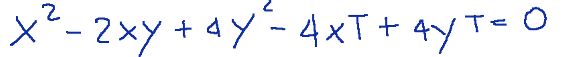
whose associated matrix is

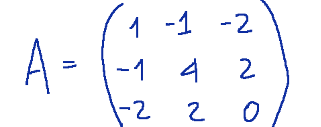
Now let's find the shape of the polar line r of the point Bit

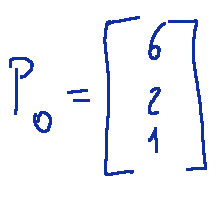
or


or

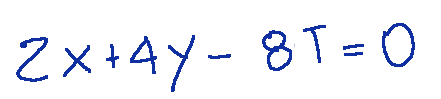
That is equivalent to

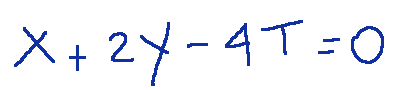
Conclusions
Polarity is a fundamental concept in analytic geometry that establishes a correspondence between points and lines in relation to a given conic (such as an ellipse, a hyperbola or a parabola).

The main conclusions regarding polarity include:
1-Relationship between points and lines
2-Reciprocity properties
3-Conic polarity
4-Classification of polarity
5-Geometric applications

Question
Do you remember that in school you studied polarity?

---

---

[ITALIAN]
30-11-2024 - Geometria analitica - Polarità [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_56)

Polarità

Descrizione
In geometria analitica, la polarità è una relazione geometrica tra punti e rette definita rispetto a una conica (ad esempio, un'ellisse, un'iperbole o una parabola). È un concetto legato alla teoria delle coniche e alle proprietà proiettive.

Definizione
Dati:
-Una conica C
Ad esempio descritta dall’equazione generale seguente

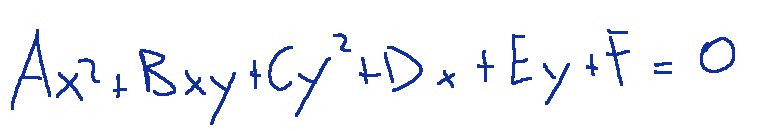
-Un punto P (x0,y0) che non appartiene alla conica
Si associa al punto P una retta polare detta polare P rispetto alla conica C. Allo stesso modo, il punto P viene chiamato polo della retta associata.

Altra definizione
Sia C una conica non degenere con matrice associata A. Dato un punto

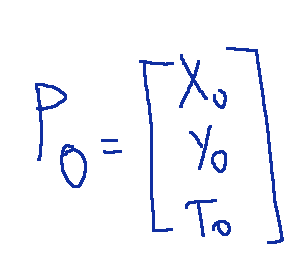
del piano proiettivo, la retta polare o, semplicemente, polare di P0 rispetto alla conica C è la retta con la forma implicita omogenea

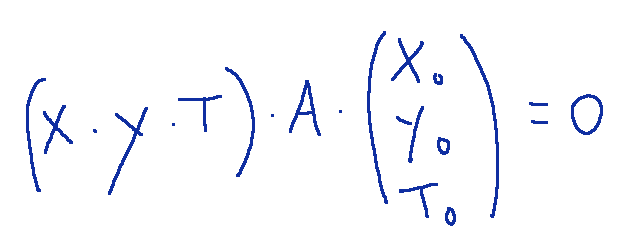
ossia

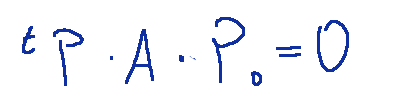
dove

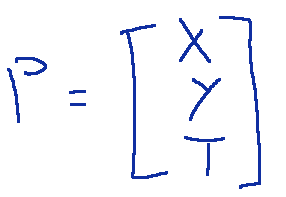
Esempio
Proviamo a considerare l’ellisse C con la seguente equazione omogenea

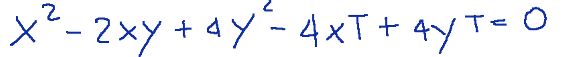
la cui matrice associata è

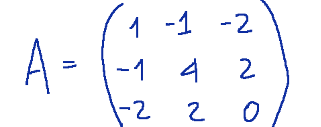
Troviamo ora la forma della retta polare r del punto Po

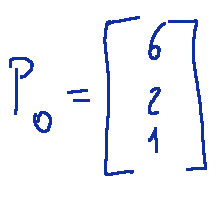
ossia

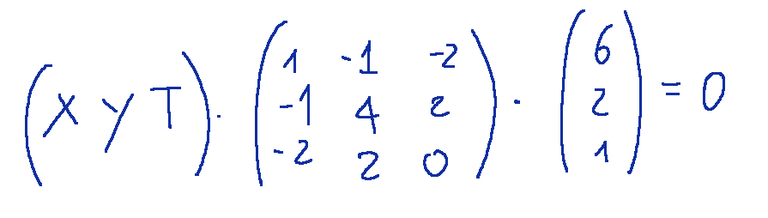
ossia

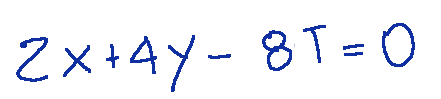
che è equivalente a

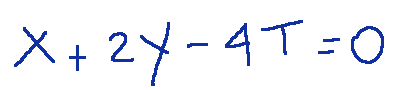
Conclusioni
La polarità è un concetto fondamentale in geometria analitica che stabilisce una corrispondenza tra punti e rette in relazione a una conica data (come un'ellisse, un'iperbole o una parabola).
Le principali conclusioni riguardo alla polarità includono:
1-Relazione tra punti e rette
2-Proprietà di reciprocità
3-Polarità conica
4-Classificazione della polarità
5-Applicazioni geometriche

Domanda
Ricordate che a scuola avete studiato la polarità?

THE END