26-10-2024 - Analytic geometry - dimension of a vector space [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
26-10-2024 - Analytic geometry - dimension of a vector space [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_090)
Dimension of a vector space
The dimension of a vector space is usually indicated as dim(V)
To better understand things, let's start from the concept regarding the dimension of a vector space. The dimension of a vector space is a measure of how big a vector space is. The dimension of a vector space will also give useful information to understand how many bases there are for vector spaces
Here below I show how the dimension of a vector space is indicated.
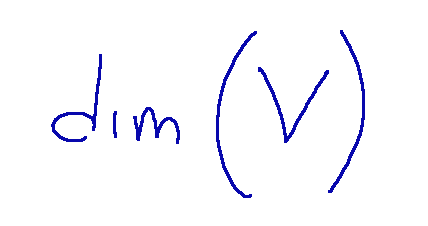
The above acronym indicates the dimension of a finitely generated vector space V which is the number of elements of any of its bases.
Let's now consider the following acronym
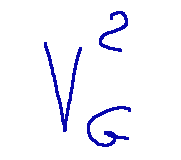
From this description we understand that the dimension is 2 and that [i,j] is a basis with 2 elements
Let's now consider the following acronym
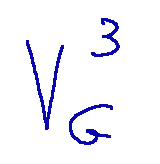
From this description we understand that the dimension is 3 and that [i,j,k] is a basis with 3 elements
Examples
As an example, below I try to ask two questions.
Is it possible to find three linearly independent geometric vectors in the following dimension?
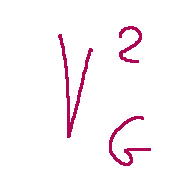
Answer
NO
It is possible to find two geometric vectors that generate the following size?
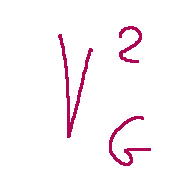
Answer
YES
Vector basis
The dimension of the vector basis is the number of linearly independent vectors {v1,...,vn} of the basis
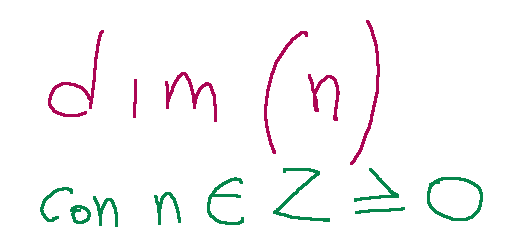
Where:
n = the cardinality.
The basis has a dimension equal to a finite number n, that is, it is composed of n vectors.
The basis has a dimension equal to infinity, that is, it is composed of infinite vectors.
Conclusions
The dimension of a vector space is a fundamental concept in linear algebra and analytic geometry, and represents the number of vectors in a basis of that space. In practical terms, the dimension of a vector space tells us how many independent vectors are needed to describe all the vectors in the space
Question
Have you ever studied the concept of dimension of a vector space in school?

[ITALIAN]
26-10-2024 - Geometria analitica - dimensione di uno spazio vettoriale [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_090)
Dimensione di uno spazio vettoriale
La dimensione di uno spazio vettoriale di solito è indicata come dim(V)
Per comprendere meglio le cose partiamo dal concetto che riguarda la dimensione di uno spazio vettoriale. La dimensione di uno spazio vettoriale è una misura di quanto è grande uno spazio vettoriale. La dimensione di uno spazio vettoriale darà informazioni utili anche per capire quante sono le basi degli spazi vettoriali
Qui di seguito mostro come è indicata la dimensione di uno spazio vettoriale.
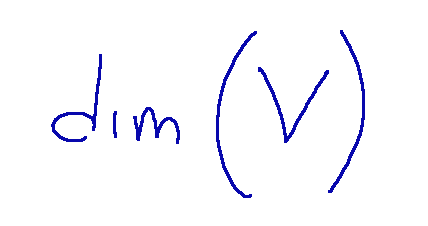
La sigla qui sopra indica la dimensione di uno spazio vettoriale finitamente generato V che è il numero degli elementi di una qualsiasi delle sue basi.
Prendiamo ora in considerazione la seguente sigla
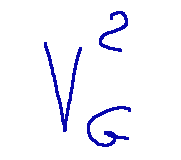
Da questa descrizione comprendiamo che la dimensione è 2 e che [i,j] è una base con 2 elementi
Prendiamo ora in considerazione la seguente sigla
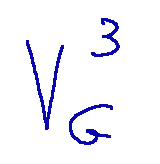
Da questa descrizione comprendiamo che la dimensione è 3 e che [i,j,k] è una base con 3 elementi
Esempi
Come esempio, qui di seguito provo a fare due domande.
È possibile trovare tre vettori geometrici linearmente indipendenti nella seguente dimensione?
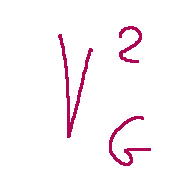
Risposta
NO
È possibile trovare due vettori geometrici che generano la seguente dimensione?
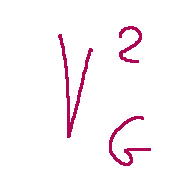
Risposta
SI
Base vettoriale
La dimensione della base vettoriale è il numero dei vettori {v1,...,vn} linearmente indipendenti della base
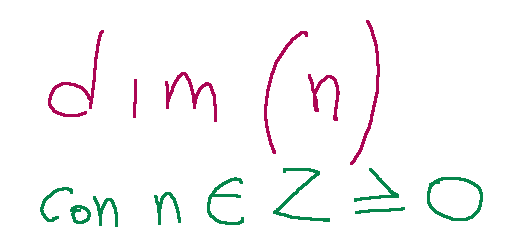
Dove:
n = la cardinalità.
La base ha una dimensione pari a un numero finito n, ossia è composta da n vettori.
La base ha una dimensione pari a infinito, ossia è composta da infiniti vettori.
Conclusioni
La dimensione di uno spazio vettoriale è un concetto fondamentale in algebra lineare e geometria analitica, e rappresenta il numero di vettori in una base di quello spazio. In termini pratici, la dimensione di uno spazio vettoriale ci dice quanti vettori indipendenti servono per descrivere tutti i vettori dello spazio
Domanda
Avete mai studiato a scuola il concetto di dimensione di uno spazio vettoriale?
THE END
Vector space is an interesting subtopic to learn about. And you did your best explaining the terms with the equations. Thanks for the lesson ad have a great weekend.
Only Mathematics and science oriented people should understand this clearly
Nice course
Come sempre utili e istruttivi questi tuoi post
!hiqvote
!discovery 30
This post was shared and voted inside the discord by the curators team of discovery-it
Join our Community and follow our Curation Trail
Discovery-it is also a Witness, vote for us here
Delegate to us for passive income. Check our 80% fee-back Program
@libertycrypto27, the HiQ Smart Bot has recognized your request (2/3) and will start the voting trail.
In addition, @stefano.massari gets !LOOL from @hiq.redaktion.
For further questions, check out https://hiq-hive.com or join our Discord. And don't forget to vote HiQs fucking Witness! 😻
lolztoken.com
Uran Utan.
Credit: vasupi
@stefano.massari, ich habe dir im Namen von @hiq.smartbot einen $LOLZ Token gesendet
Verwende den Befehl !WITZ oder !LOOL, um einen Witz und ein $LOLZ zu teilen.
NEW: Join LOLZ's Daily Earn and Burn Contest and win $LOLZ
.(8/8)
!HOPE
!LOL
!INDEED
lolztoken.com
Me: I would say my biggest weakness is listening.
Credit: reddit
@stefano.massari, I sent you an $LOLZ on behalf of cryptoyzzy
(7/10)
Delegate Hive Tokens to Farm $LOLZ and earn 110% Rewards. Learn more.
(2/5)
@stefano.massari! @cryptoyzzy Wants to spread Hope! so I just sent 1 HOP to your account on behalf of @cryptoyzzy.
Since we think the world can use more Hope, you can now already start spreading Hope yourself!
(7/10)
@stefano.massari! @cryptoyzzy Totally agrees with your content! so I just sent 1 IDD to your account on behalf of @cryptoyzzy.
https://x.com/lee19389/status/1850590971878089211
#hive #posh
(2/5)
@stefano.massari! @cryptoyzzy Wants to spread Hope! so I just sent 1 HOP to your account on behalf of @cryptoyzzy.
Since we think the world can use more Hope, you can now already start spreading Hope yourself!