21-10-2024 - Linear Algebra - Independence of Column Vector [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH
21-10-2024 - Linear Algebra - Independence of Column Vector [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_092)
independence of column vectors
After the article of 19-10-2024 let's now try to make two examples. One where we see linearly independent column vectors and one where we see linearly dependent column vectors.
Linearly independent column vectors
Let's consider the following three column vectors in R3
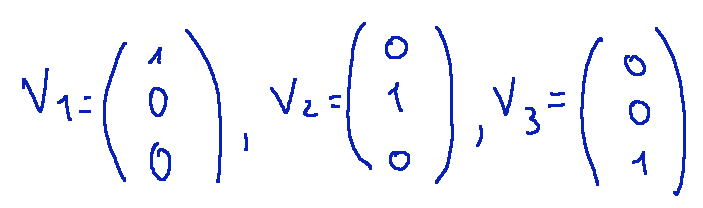
In this case we can see that there is no column vector that can be expressed as a linear combination of the other two.
We can therefore say that they are linearly independent.
To verify this, let's think about the following equation where we insert the coefficients c.
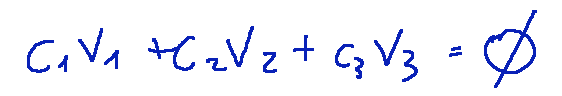
This represented with the form of column vectors looks like this:
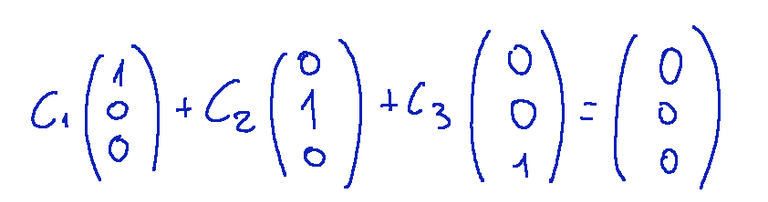
To demonstrate this equation we will have the following result.
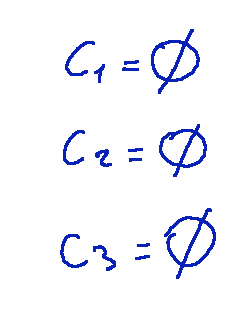
Since the only solution is that all coefficients are zero, the vectors are linearly independent.
Linearly dependent column vectors
Let's write two linearly dependent column vectors below and then analyze them.
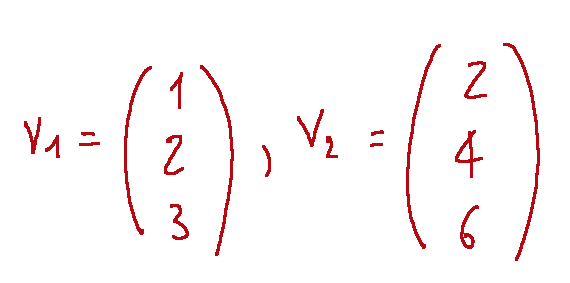
In this case we can easily notice the following
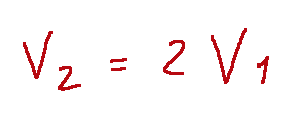
The vector v2 is a linear combination of v1 with the coefficient of 2.
So these two column vectors are linearly dependent.
Below I try to describe it algebraically
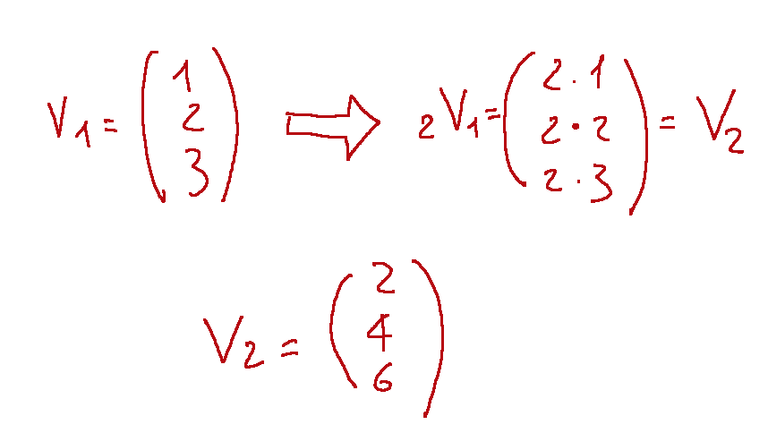
Conclusions
A set of linearly independent column vectors is such if none of them can be written as a linear combination of the others.
Question
Have you ever covered the topic of linearly independent column vectors at school?

[ITALIAN]
21-10-2024 - Algebra lineare - indipendenza dei vettori colonna [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_092)
indipendenza dei vettori colonna
Dopo l'articolo del 19-10-2024 proviamo ora a far due esempio. Uno dove vediamo vettori colonna linearmente indipendenti ed uno dove vediamo vettori colonna linearmente dipendenti.
Vettori colonna linearmente indipendenti
Consideriamo i seguenti tre vettori colonna in R3
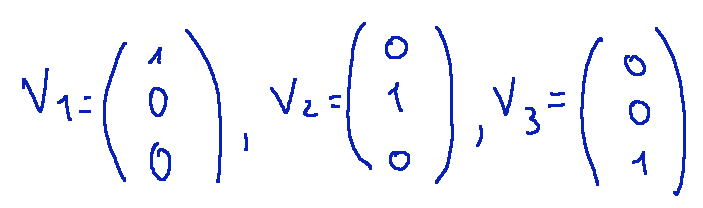
In questo caso possiamo vedere che non c'è un vettore colonna che può essere espresso come combinazione lineare degli altri due.
Possiamo quindi affermare che sono linearmente indipendenti.
Per verificarlo pensiamo alla seguente equazione dove inseriamo i coefficienti c.
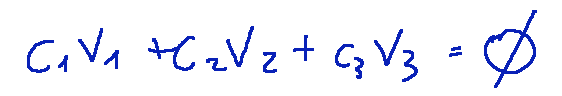
Questo rappresentato con la forma dei vettori colonna si mostra così:
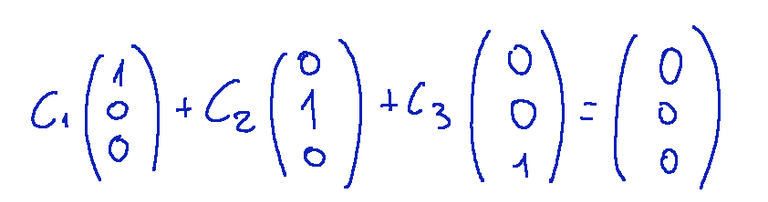
Per dimostrare questa equazione avremo il seguente risultato.
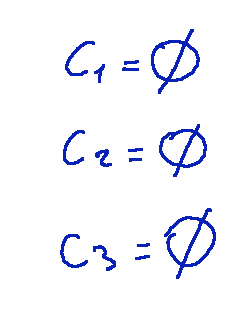
Poiché l'unica soluzione è che tutti i coefficienti sono zero, i vettori sono linearmente indipendenti.
Vettori colonna linearmente dipendenti
Scriviamo qui di seguito due vettori colonna linearmente dipendenti e poi li andremo ad analizzare.
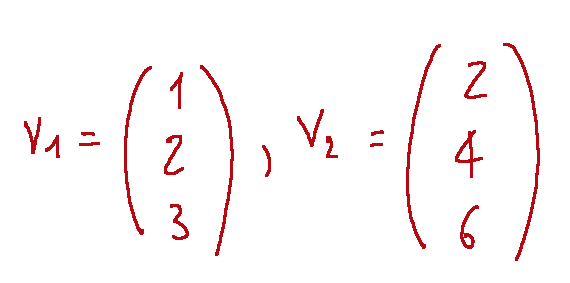
In questo caso possiamo facilmente notare quanto segue
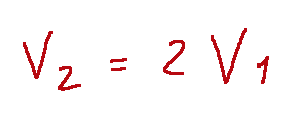
Il vettore v2 è una combinazione lineare di v1 con il coefficiente di 2.
Quindi questi i due vettori colonna sono linearmente dipendenti.
Qui di seguito provo a descrivere la cosa in maniera algebrica
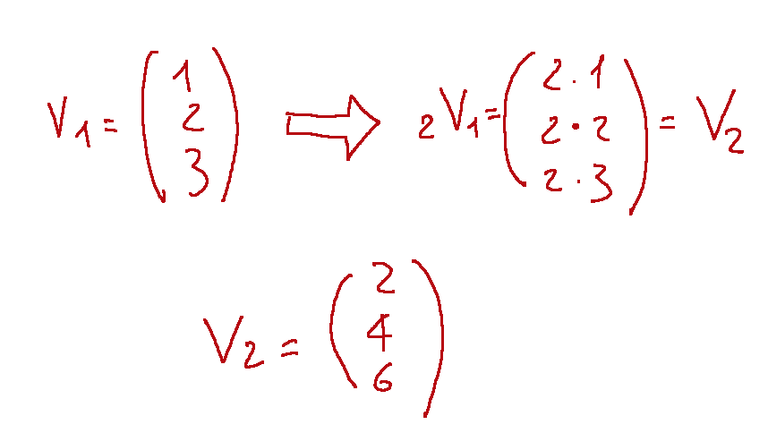
Conclusioni
Un insieme di vettori colonna linearmente indipendenti è tale se nessuno di essi può essere scritto come combinazione lineare degli altri.
Domanda
Avete mai trattato a scuola l'argomento dei vettori colonna linearmente indipendenti?
THE END
Mathematics used to be my favorite subject. I still love it though I don't teach in the classroom anymore
Thanks for stopping by, so you were a teacher? Why don't you score anymore?
Algebra is an interesting aspect of mathematics especially Linear Algebra. It's sure fun studying vectors and numbers and making calculations out of them. I fiddled a little with this topic some years ago. Thanks for the lesson and have a great day.
Thanks for leaving a comment. These topics in my opinion are also useful to develop a bit of logic
https://x.com/lee19389/status/1848495299393663303
#hive #posh
!discovery 30
!HOPE
!LOL
!INDEED
lolztoken.com
I can also tell if they’re standing.
Credit: reddit
@stefano.massari, I sent you an $LOLZ on behalf of cryptoyzzy
(6/10)
NEW: Join LOLZ's Daily Earn and Burn Contest and win $LOLZ
(1/5)
@stefano.massari! @cryptoyzzy Wants to spread Hope! so I just sent 1 HOP to your account on behalf of @cryptoyzzy.
Since we think the world can use more Hope, you can now already start spreading Hope yourself!
(6/10)
@stefano.massari! @cryptoyzzy Totally agrees with your content! so I just sent 1 IDD to your account on behalf of @cryptoyzzy.