10-12-2024 - Computer science basics - Boolean algebra [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH
10-12-2024 - Computer science basics - Boolean algebra [EN]-[IT]
With this post I would like to give a brief instruction on the topic mentioned in the subject
(code notes: X_95)

Boolean algebra
BOOLINE ALGEBRA
Boolean algebra takes its name from the English mathematician George Boole (1815-1864) and is a particular type of algebra in which variables and functions can only assume the values ​​0 and 1. Precisely because of this characteristic, Boolean algebra is essential for the development of electronic calculators because it describes all the operations that can be done with bits.
A Boolean variable is a binary variable that can assume only two logical values, 0 and 1.

Boolean algebra is applied in digital logic, programming and set theory.

In Boolean algebra there are 3 fundamental operations:
1-AND (∧): Returns 1 only if both operands are 1 (logical conjunction).

2-OR (∨): Returns 1 if at least one of the operands is 1 (logical disjunction).

3-NOT (¬): Inverts the logical value (negation).

Let's take into account the following tables:
The logical AND operation follows this truth table:

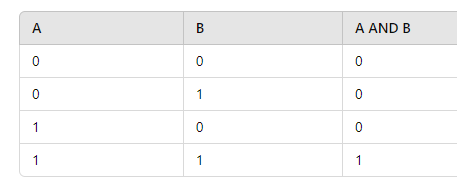
The logical OR operation follows this truth table:

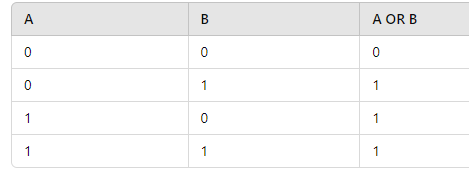
Exercise 1
The operation Logical OR between two inputs A and B returns 0 if
A and B are 0

Exercise 2
The logical AND operation between two inputs A and B returns 1 if
A and B are 1

Exercise 3
Here is a conversion exercise.
Let's try to express the following decimal number in a binary number representing the modulus and the sign on 10 bits.
The number is -31.

Let's start with the search for the binary number by progressively dividing the number 31

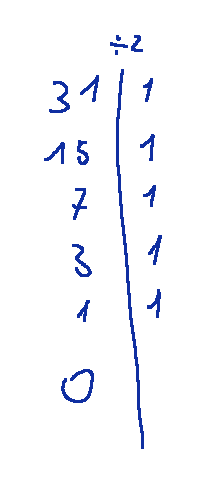
Module and sign
The first bit indicates the sign and the following must be taken into account:
0 for a positive number.
1 for a negative number.
The remaining 9 bits represent the absolute value in binary

Converting 31 to binary
From the calculations above, we can say that the number 31 in binary is 11111 (5 bits)

Adding the missing bits
We need to use 9 bits for the absolute value, so we add four zeros to the left:
0000011111

Adding the sign bit
Since the number is negative, the sign bit will be 1.

Final result (10 bits)
1 0000011111

Conclusions
Boolean algebra is a mathematical structure used to represent and manipulate logical values, developed by George Boole in the 19th century. It is based on two main states, generally referred to as 0 (false) and 1 (true).

Question
Did you study Boolean operations (fundamental operations used in Boolean logic) in school?

---

---

[ITALIAN]
10-12-2024 - Basi di informatica - L’algebra di Boole [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_95)

L’algebra di Boole
ALGEBRA DI BOOLE
L’algebra di Boole prende il nome dal matematico inglese George Boole (1815-1864) ed è un particolare tipo di algebra in cui variabili e funzioni possono assumere solo i valori 0 e 1. Proprio per questa sua caratteristica, l’algebra di Boole è essenziale per lo sviluppo dei calcolatori elettronici poiché descrive tutte le operazioni che è possibile fare con i bit.
Un variabile booleana è una variabile binaria che può assumere solo due valori logici, 0 e 1.

L'algebra di Boole viene applicata nella logica digitale, nella programmazione e nella teoria degli insiemi.

Nell'algebra di Boole esistono 3 operazioni fondamentali:
1-AND (∧): Restituisce 1 solo se entrambi gli operandi sono 1 (congiunzione logica).

2-OR (∨): Restituisce 1 se almeno uno degli operandi è 1 (disgiunzione logica).

3-NOT (¬): Inverte il valore logico (negazione).

Teniamo conto delle seguenti tabelle:
L'operazione AND logico segue questa tabella di verità:

L'operazione OR logico segue questa tabella di verità:

Esercizio 1
L'operazione OR logico tra due ingressi A e B restituisce 0 se
A e B valgono 0

Esercizio 2
L'operazione AND logico tra due ingressi A e B restituisce 1 se
A e B valgono 1

Esercizio 3
Qui di seguito un esercizio di conversione.
Proviamo ad esprimere il seguente numero decimale in un numero binario rappresentando il modulo e il segno su 10 bit.
Il numero è -31.

Iniziamo con la ricerca del numero binario dividendo progressivamente il numero 31

Modulo e segno
Il primo bit indica il segno e si deve tenere conto di quanto segue:
0 per un numero positivo.
1 per un numero negativo.
I restanti 9 bit rappresentano il valore assoluto in binario

Conversione di 31 in binario
Dai calcoli svolti prima possiamo dire che il numero 31 in binario è 11111 (5 bit)

Aggiunta dei bit mancanti
Dobbiamo usare 9 bit per il valore assoluto, quindi aggiungiamo quattro zeri a sinistra:
0000011111

Aggiunta del bit di segno
Poiché il numero è negativo, il bit di segno sarà 1.

Risultato finale (10 bit)
1 0000011111

Conclusioni
L'algebra di Boole è una struttura matematica utilizzata per rappresentare e manipolare valori logici, sviluppata da George Boole nel XIX secolo. Si basa su due stati principali, generalmente indicati come 0 (falso) e 1 (vero).

Domanda
Avete studiato a scuole le operazioni booleane (operazioni fondamentali utilizzate nella logica booleana)?

THE END