03-12-2024 - Analytical Geometry - Differentiable Curves [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

ENGLISH
03-12-2024 - Analytical Geometry - Differentiable Curves [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_52)

Differentiable Curves

What are they for
Differentiable curves in space are fundamental in physics, because they represent the trajectories of particles moving in space.

Definition
To define differentiable curves, we must consider derivable functions

whose derivative is indicated by f’. We can say that a polynomial

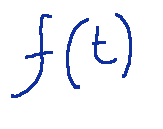
in the variable t, is differentiable and its derivative f’(t) is the partial derivative with respect to the variable t, i.e. the polynomial

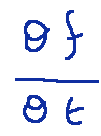
The functions

so that the derivative exists for every

are said to be differentiable.
Polynomials are differentiable functions.

Algebraic definition
A differentiable curve in Euclidean space is a function

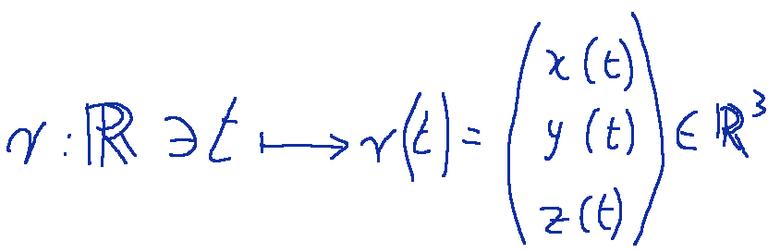
Consider the following.
With x(t), y(t), z(t) differentiable functions. The variable t is called the parameter of the curve.
The points of the image of the function are called points of the curve.

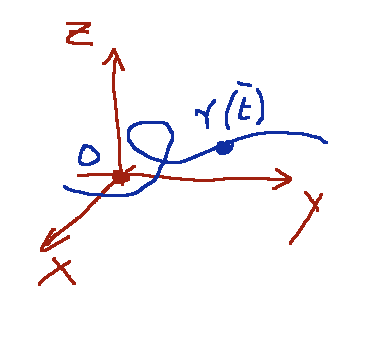
differentiable curves in the Euclidean plane R2
We can also consider differentiable curves in the Euclidean plane R2

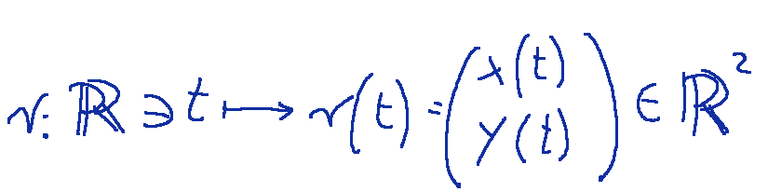
with x(t), y(t) differentiable functions, but they are only a particular case of the curves differentiable in Euclidean space, where z(t) = 0 for every t in R

Conclusions
In analytic geometry, a differentiable curve is a curve described by a function that is continuous and has continuous derivatives on an interval.

Question
Do you remember having ever done some exercises in school about differentiable curves

[ITALIAN]
03-12-2024 - Geometria analitica - Curve differenziabili [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_52)

Curve differenziabili

A cosa servono
Le curve differenziabili nello spazio sono fondamentali in fisica, perché rappresentano le traiettorie delle particelle che si muovono nello spazio.

Definizione
Per definire le curve differenziabili bisogna considerare funzioni derivabili

la cui derivata è indicata con f’. Possiamo dire che un polinomio

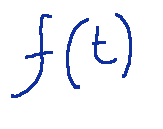
nella variabile t, è derivabile e la sua derivata f’(t) è la derivata parziale rispetto alla variabile t, ossia il polinomio

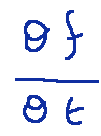
Le funzioni

per cui la derivata esiste per ogni

sono dette differenziabili.
I polinomi sono funzioni differenziabili.

Definizione algebrica
Una curva differenziabili nello spazio euclideo è una funzione

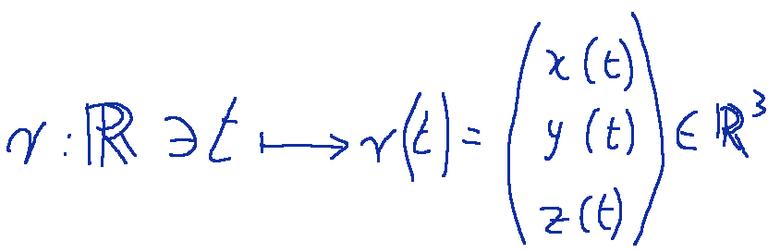
Da considerare quanto segue.
Con x(t), y(t), z(t) funzioni differenziabili. La variabile t è detta parametro della curva.
I punti dell’immagine della funzione sono detti punti della curva.

curve differenziabili nel piano euclideo R2
Possiamo anche considerare curve differenziabili nel piano euclideo R2

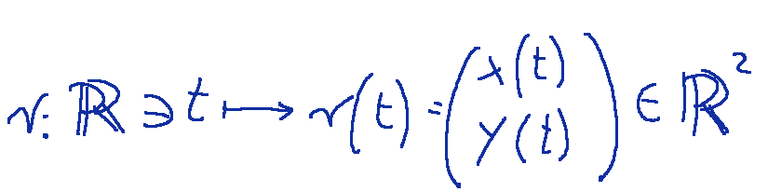
con x(t), y(t) funzioni differenziabili, ma esse sono solo un caso particolare delle curve differenziabili nella spazio euclideo, dove z(t) = 0 per ogni t che appartiene ad R

Conclusioni
In geometria analitica, una curva differenziabile è una curva descritta da una funzione che è continua e ha derivate continue su un intervallo.

Domanda
Ricordate di aver mai fatto qualche esercizio a scuola a riguardo delle curve differenziabili

THE END