Generando epicicloides (Cardioide) con GeoGebra
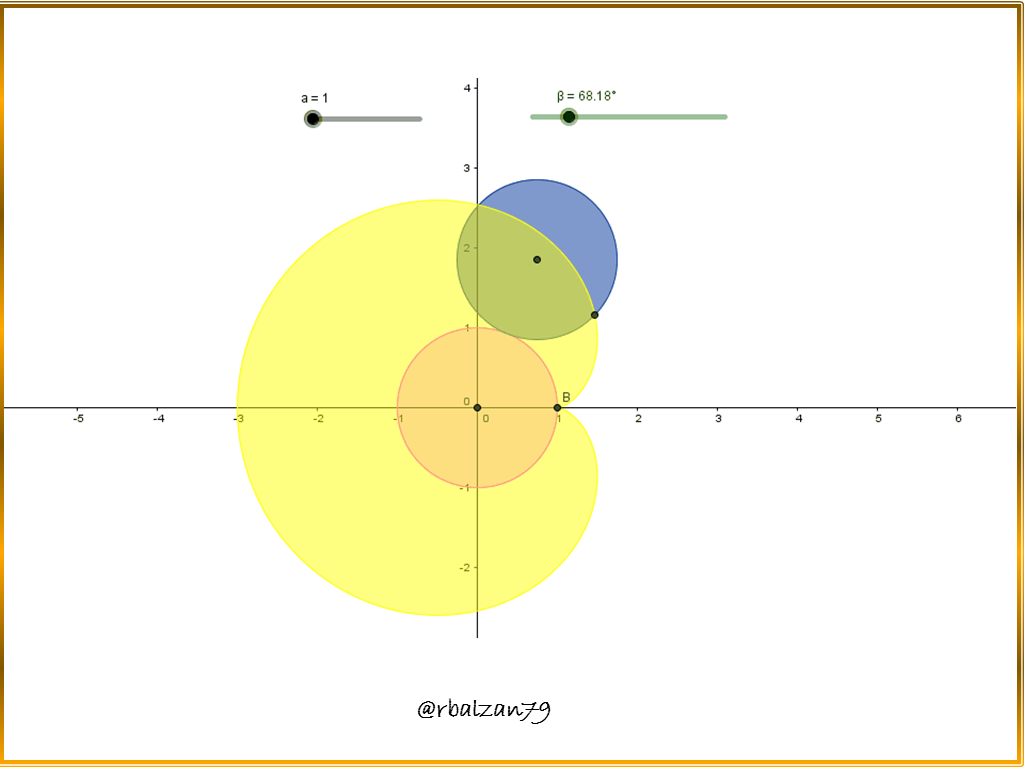
Al igual que con la cicloide, es importante relacionarnos con algunas de las características de la curva epicicloide, y para ello podemos expresar que esta curva no la generaremos sobre una superficie recta, por lo tanto, tenemos que para lograr dibujar a una epicicloide es necesario constar con dos circunferencia, una denominada generatriz y la otra directriz, de esta manera haremos girar sin resbalar una circunferencia sobre otra.
Unas de las más resaltantes características de dicha curva epicicloide es que sirve como base fundamental para el diseño de dientes para engranajes y cuando logremos realizar nuestra imagen visualizaremos el denominado movimiento epicicloidal el cual es semejante a la de una rueda dentada sobre otra.
Por lo tanto, ya conocida algunas de las características de esta extraordinaria curva epicicloide, es necesario pasar a la descripción de la realización de dicha curva en particular como hemos dicho de la cardioide, y la misma, como podrán observar más adelante posee forma de corazón.
Paso 1:
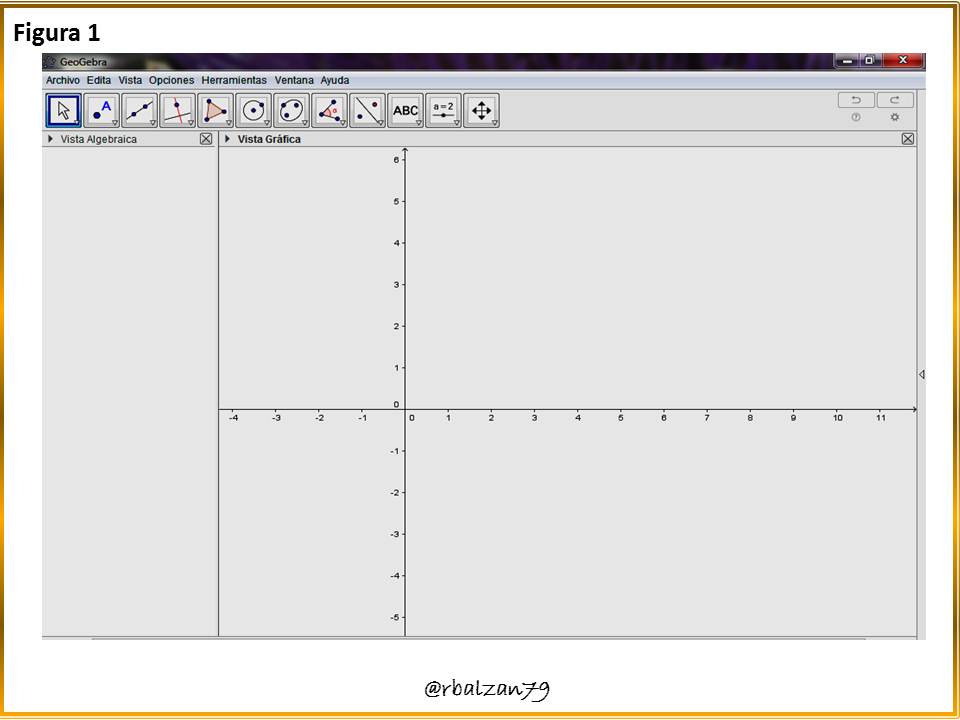
Abrimos GeoGebraPaso 2:
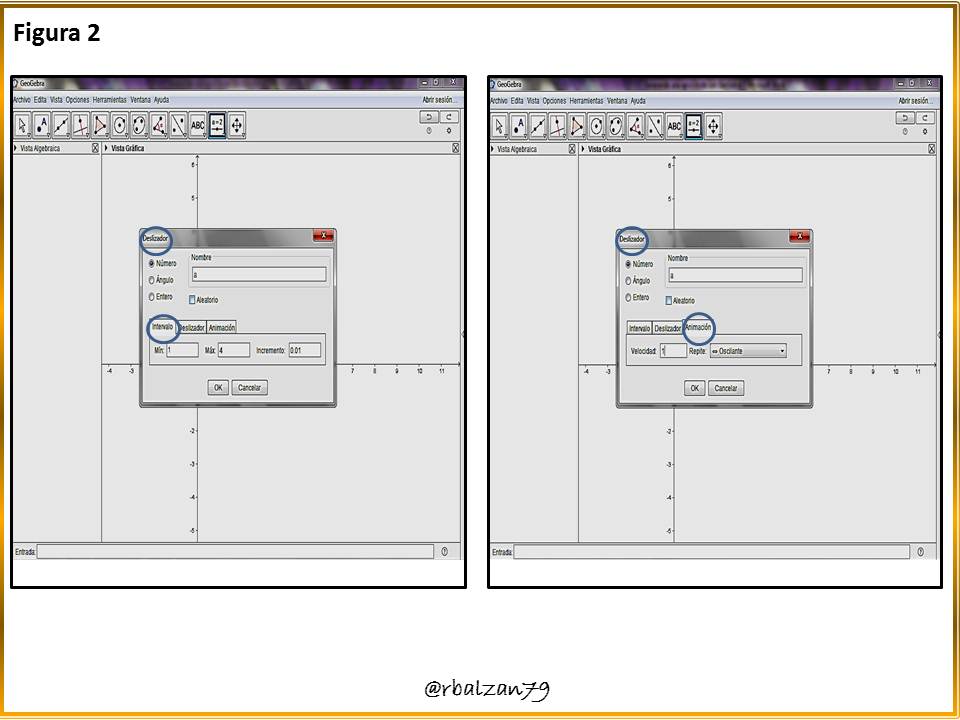
Creamos un deslizador, para el intervalo y la forma de movimiento a realizar, como podrán observar a continuación en la siguiente figura 2.Paso 3:
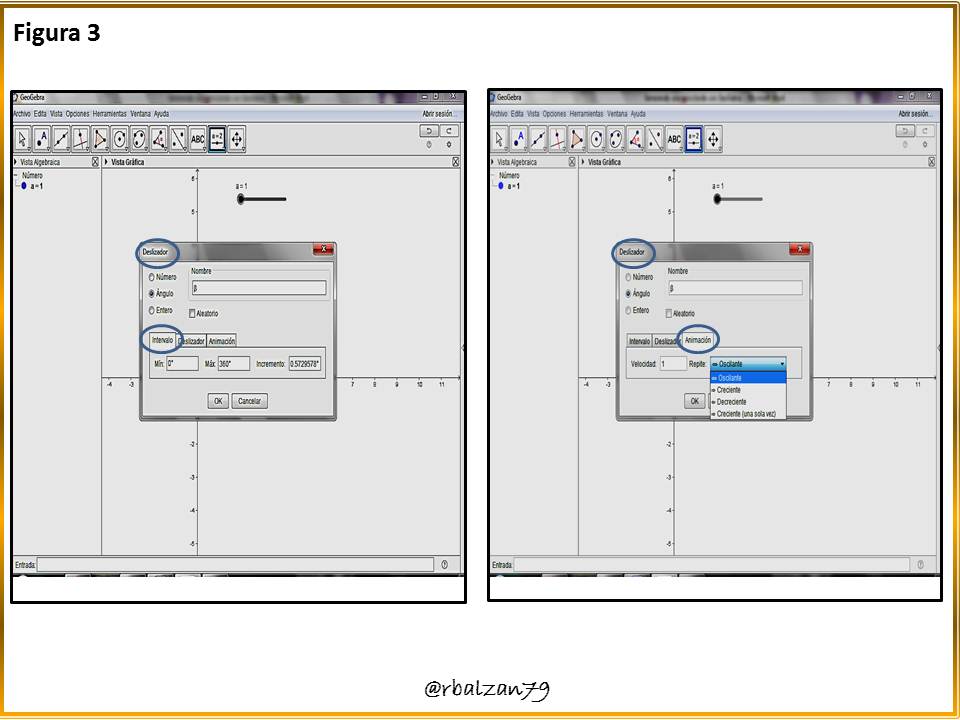
Es necesario Crear otro deslizador para el ángulo, por lo tanto, establecemos los intervalos del mismo en la siguiente figura 3.Paso 4:
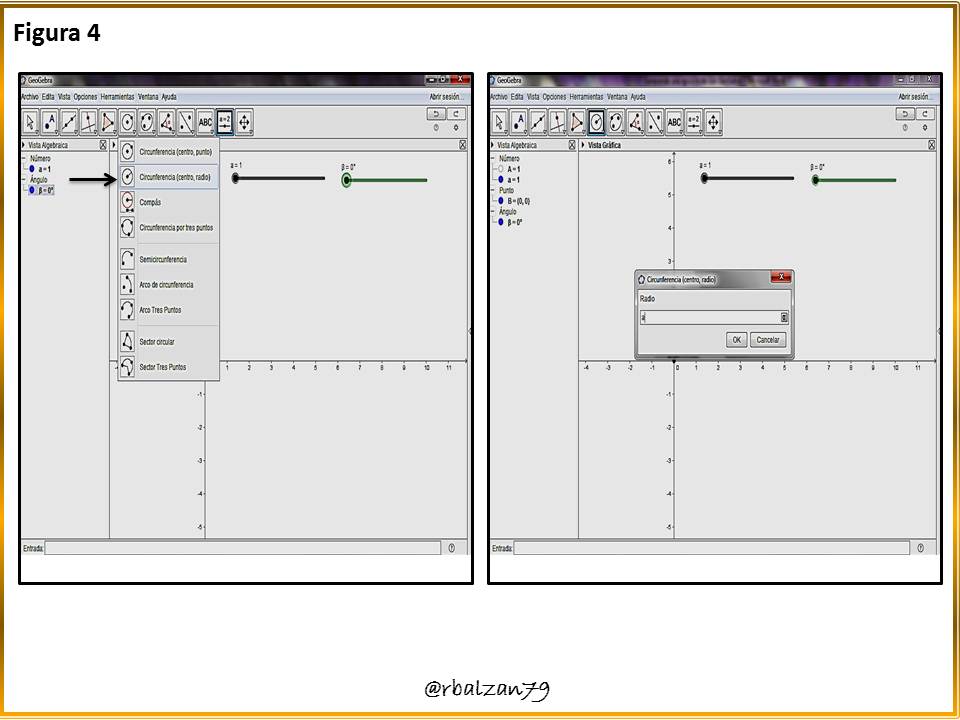
Creamos nuestra circunferencia directriz, como se observar en la figura 4.Paso 5:
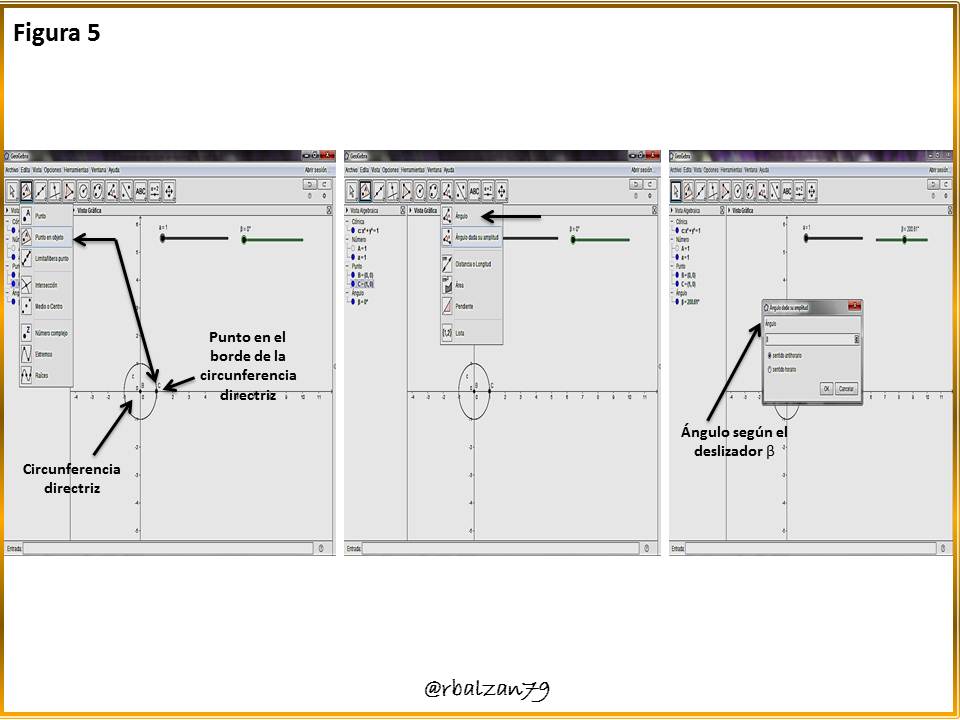
Ahora creamos un punto en el borde de la circunferencia directriz y le asignamos un ángulo de giro, como podemos visualizar en la siguiente figura 5.Paso 6:
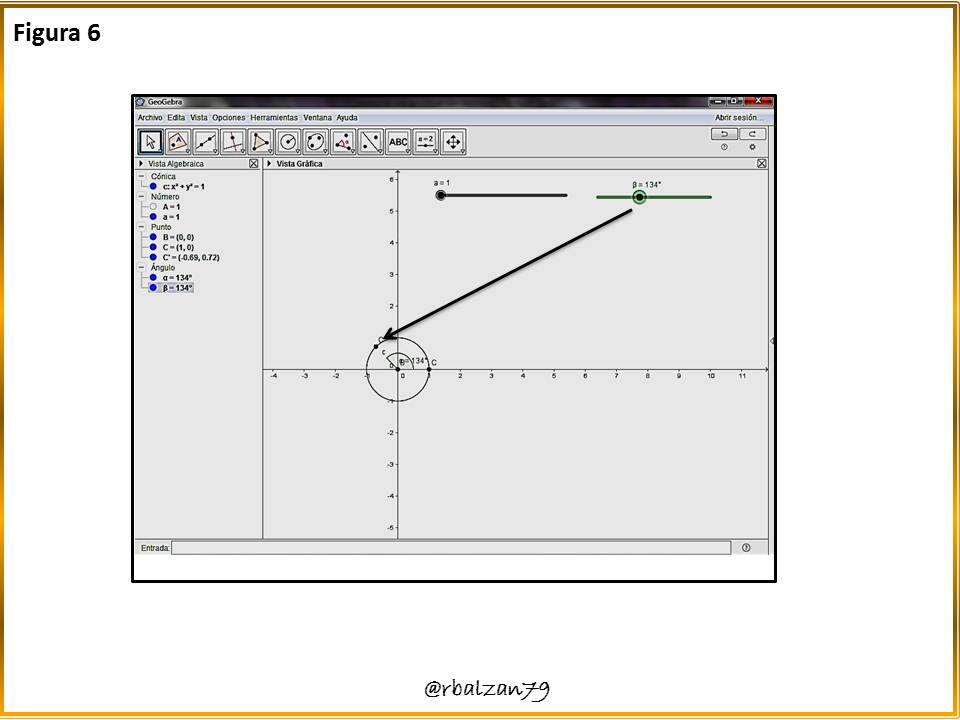
Al mover nuestro deslizador ángulo (β) observamos como el punto al borde la circunferencia se moviliza, como observan en la figura 6.Paso 7:
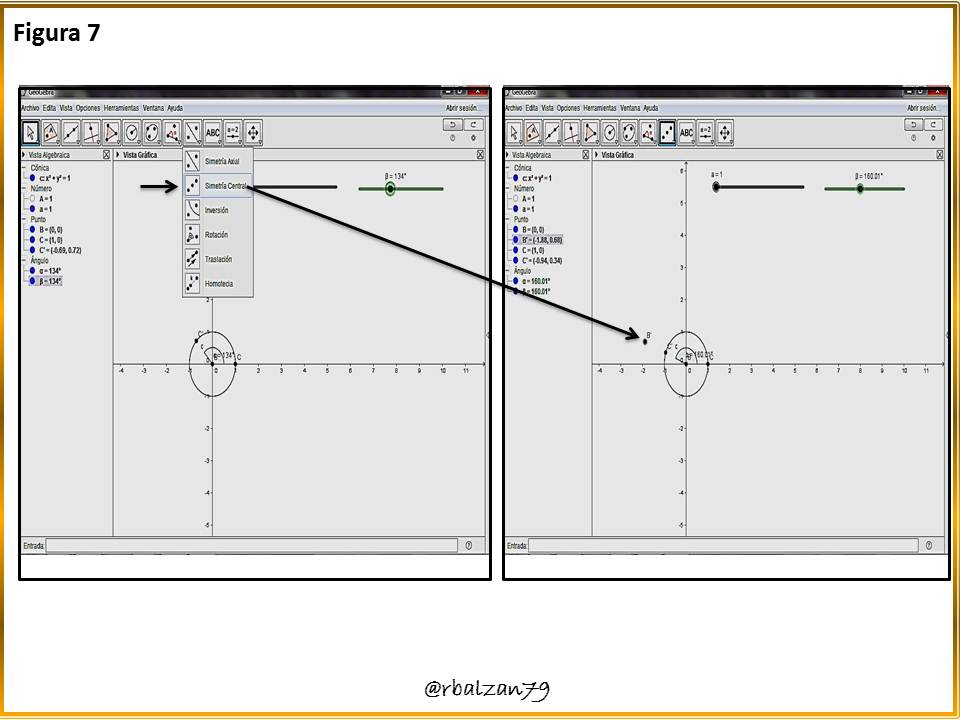
Pero para generar una epicicloide debemos tener dos circunferencias, por lo tanto, procedemos a realizar una simetría del punto centro de la circunferencia generatriz con el punto al borde de la circunferencia, como se observa en la figura 7.Paso 8:
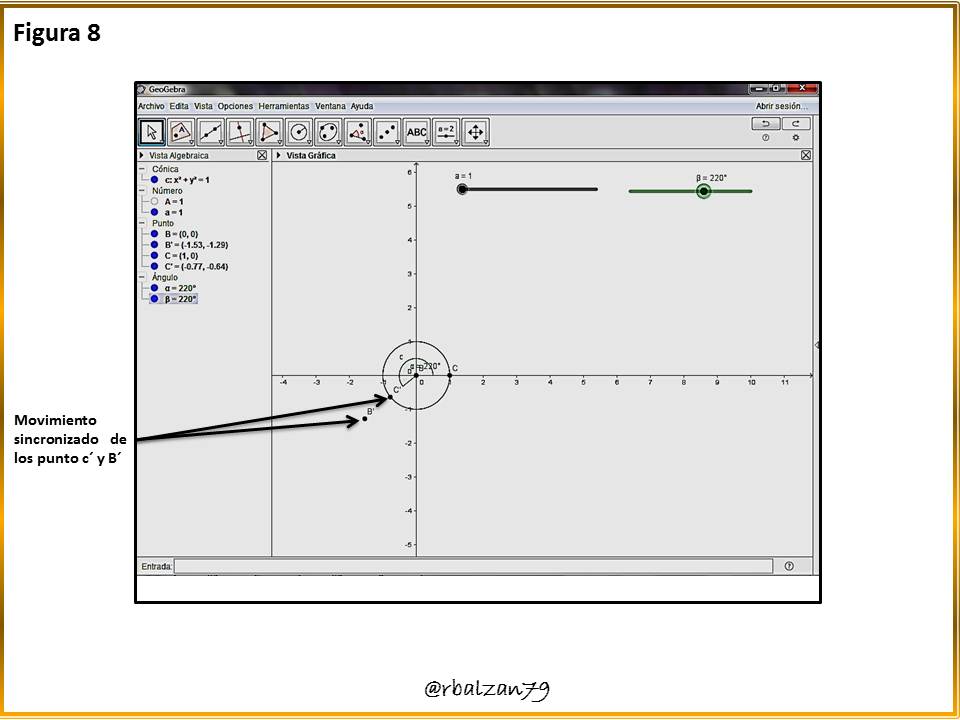
El anterior paso nos permite mover de manera sincronizada el punto simétrico con el punto al borde de la circunferencia generatriz, como observan en la figura 8.Paso 9:
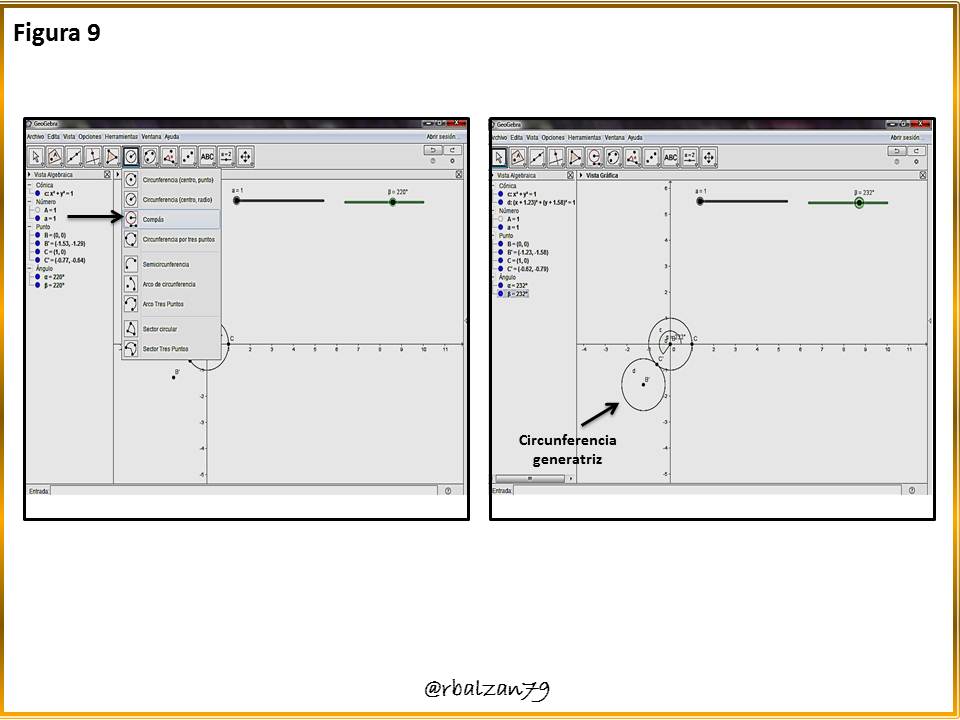
Ahora podemos construir nuestra circunferencia generatriz cuyo centro sería el punto simetría del punto en el borde de la circunferencia directriz, como se observa a continuación en la figura 9.paso 10:
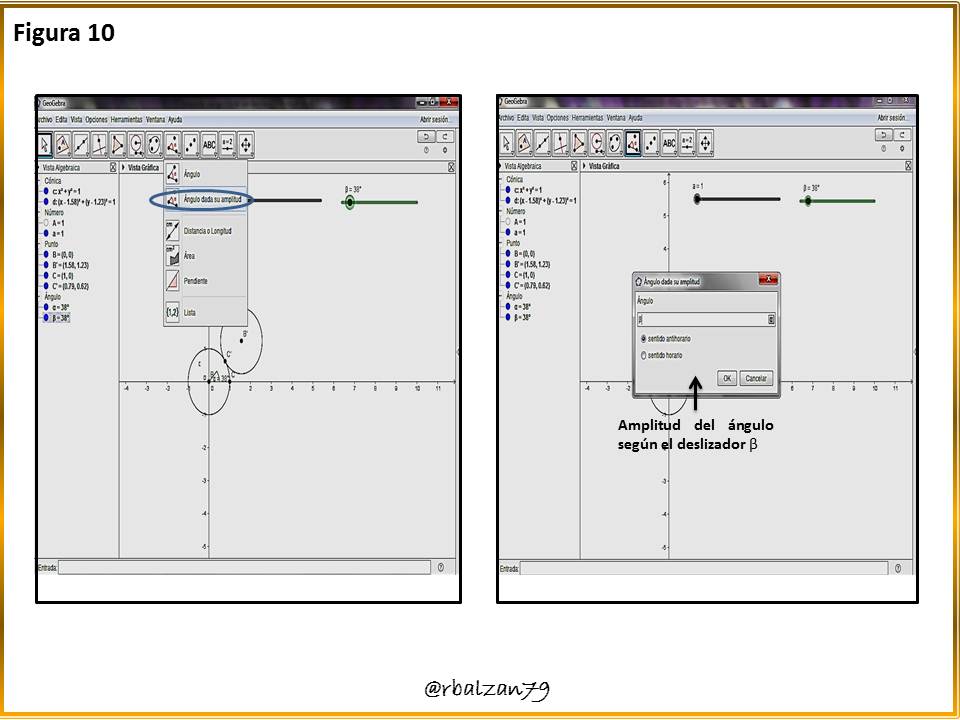
Ahora le asignamos el ángulo de giro al punto generador de nuestra epicicloide que en este caso sería una cardioide, como observan en la figura 10.paso 11:
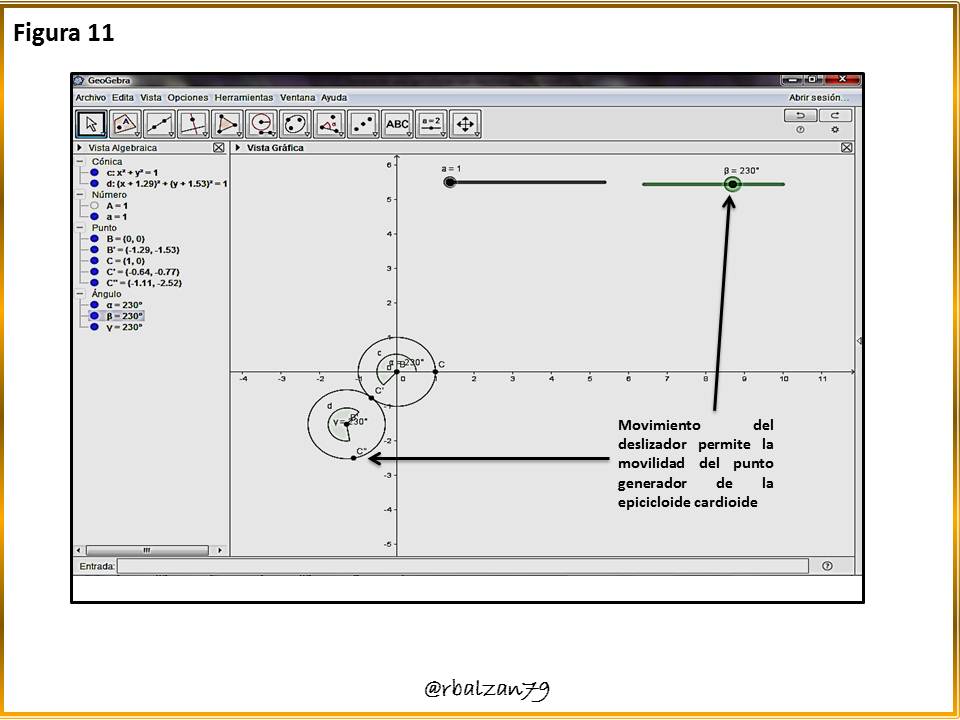
El paso anterior nos permite asignarle movimiento al punto generador de la epicicloide como pueden observar en la siguiente figura 11.Paso 12:
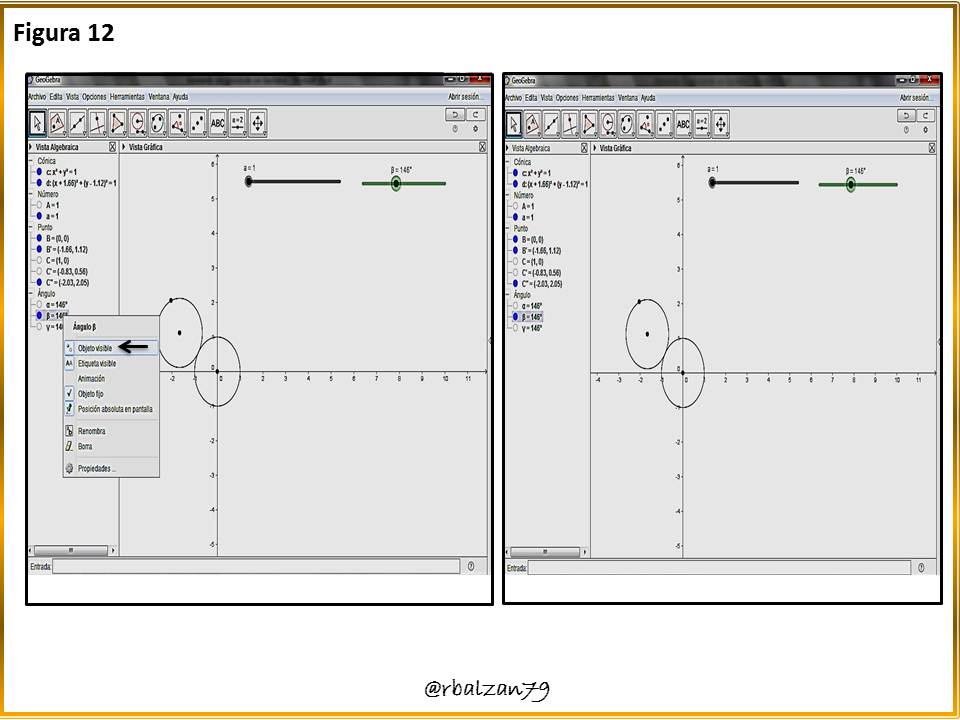
Antes de describir el lugar geométrico de la epicicloide como la cardioide podemos ocultar algunos rasgos como; los ángulos y literales de nuestros puntos, como se observa a continuación en la siguiente figura 12.Paso 13:
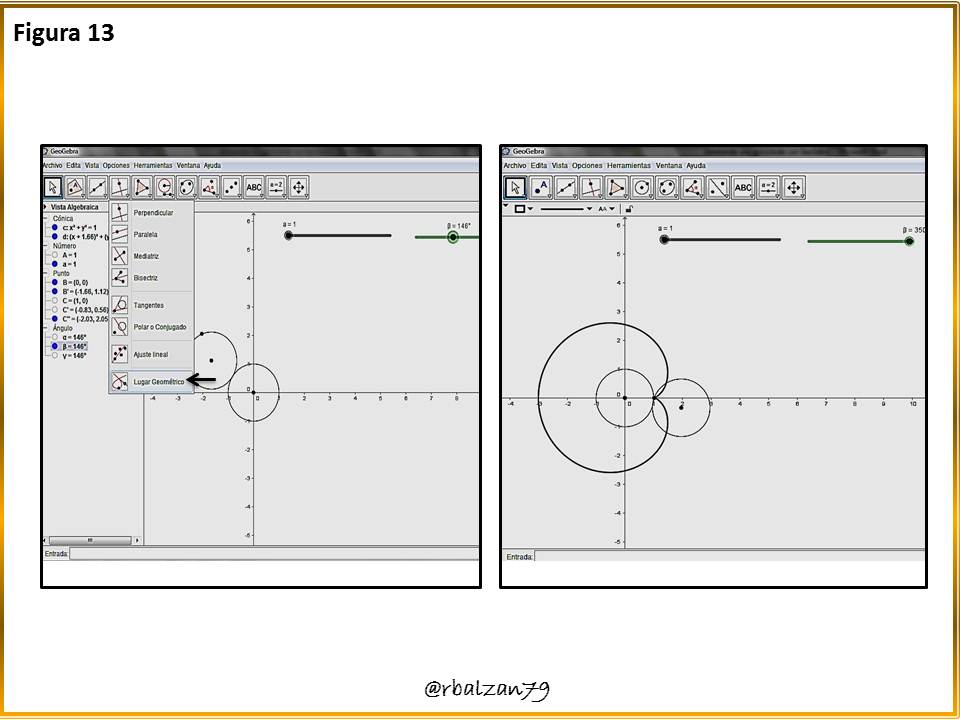
Ahora activamos la opción para dibujar el lugar geométrico de la epicicloide que en este caso es la cardioide, como se observa en la siguiente figura 13.Paso 14:
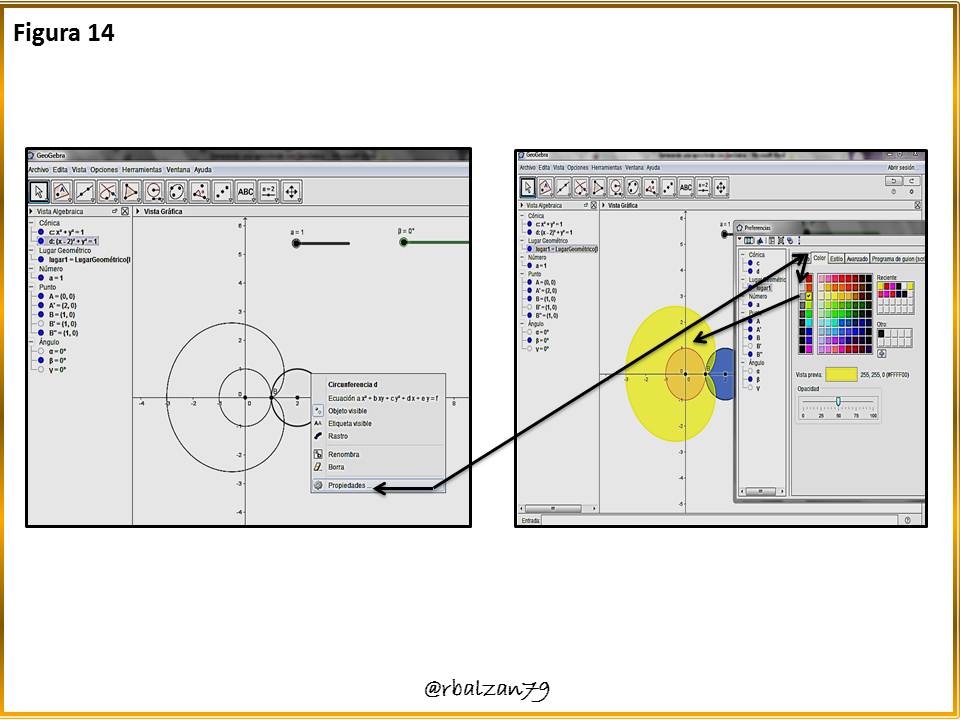
Podemos realizar algunas modificaciones como pueden ver a continuación en la figura 14.De esta manera generamos nuestra epicicloide denominada cardioide la cual observamos al inicio de este tutorial, y la misma como podrán visualizar se asemeja a un corazón, resaltando que nuestras principales herramientas como pudieron observar fueron; GeoGebra y nuestra creatividad.
Hasta otra oportunidad mis queridos y apreciados lectores.
Nota: Todas las imagines fueron obtenidas en GeoGebra y llevadas a presentación Power Point.
Referencia bibliográfica recomendada
[1]GeoGebra
Su post ha sido valorado por @ramonycajal
Gracias al curador @ramonycajal por el valioso apoyo e igualmente a toda la comunidad de Cervantes. Saludos.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Thank you dear community for your support. Best regards.