Volumen de un paraboloide mediante integrales dobles
Hola amigos, en esta oportunidad les voy a enseñar cómo calcular el volumen de un paraboloide mediante integrales dobles.
Para este caso vamos a conocer la ecuación del paraboloide al que le vamos a calcular el volumen:
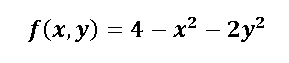
Como se puede apreciar es una función de dos variables, por lo que su gráfica es el sistema tridimensional, para el caso de este post me voy a apoyar con el uso del software libre de geogebra 5.0, en el cual colocamos la ecuación en la entrada y nos genera automáticamente el gráfico, el cual les presento a continuación:
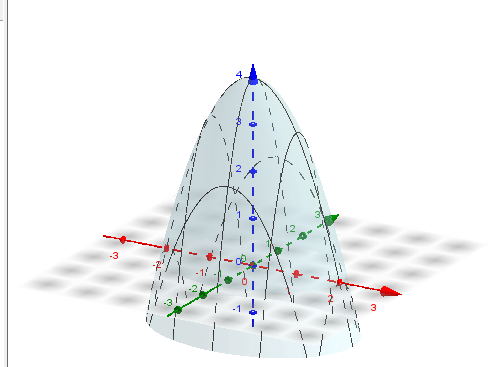
Cómo se puede observar en la imagen anterior, el paraboloide de la ecuación presentada representa la de un paraboloide elíptico, al cual se le va a calcular su volumen entre el paraboloide y el plano x,y.
Los pasos para calcular el volumen entre el paraboloide elíptico y el plano x,y son los siguientes:
[1] Hacemos z=0 para delimitar la región del plano x,y.
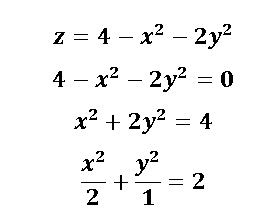
Tenemos que la región del plano x,y es una elipse que está limitada por el eje x en el siguiente rango:
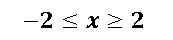
Para saber la región limitada por el plano x,y, simplemente hacemos Z=0, y nos damos cuenta que las cotas para y son:
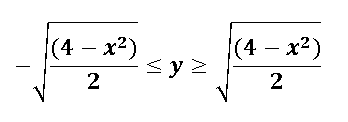
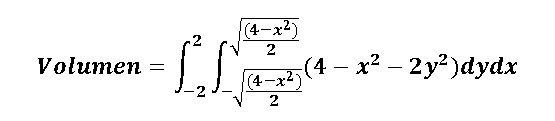
[2] Nos planteamos la integral de la siguiente forma:
[3] Se resuelve la integral realizando un cambio de sistemas, es decir cambiamos las variables del sistema cartesiano a un sistema de coordenadas polares, quedándonos lo siguiente:
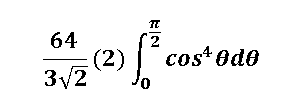
Resolviendo esta integral por el método de funciones trigonométricas y aplicando el teorema fundamental del cálculo para integrales definidas nos queda que el volumen es igual a:
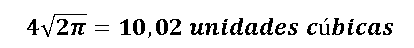
Referencias consultadas y recomendadas
Cálculo completo Vol 1 y 2 9na Edición Ron Larson & Bruce H. Edwards

Su post ha sido valorado por @goya
Gracias por el apoyo a todo el equipo de cervantes. Saludos
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Gracias por el apoyo al equipo de StemSocial. Saludos
Estamido @carlos84 es un placer leerte.
Tengo que resaltar que me encantan este tipo de publicaciones, tienen la capacidad primero de hacerme recordar cosas que pende había olvidado, pero que no, siguen allí y es un claro ejemplo de que cando las cosas se aprenden bien, nunca se olvidan.
Segundo, me trasladan inmediatamente a mi época universitaria, parece que me encuentro sentada dentro del ambiente de clases viviendo toda esa experiencia nuevamente. Gracias por compartirlo.
Hola mi estimada amiga @hannymarchan.
Es un honor para mi la visita y lectura de este post, que bueno que tengas tan buenos recuerdos de la universidad cuando lees este tipo de contenido.
Saludos y un gran abrazo.