Regla de L'hopital para límites algebraicos indeterminados de la forma 0/0
Hola amigos de la comunidad hive.
En esta oportunidad les traigo otro tema de cálculo y que los estudiantes ahora en tiempo de pandemia se pueden beneficiar enormemente, para explicar la regla de L'hopital para límites indeterminados quiero exponer el ejemplo de una función algebraica cuyo límite es de la forma indeterminada 0/0.
Para ello me gusta resolver como de costumbre los ejercicios propuestos del libro de cálculo de Larson, para ello es importante que si tienes el libro en PDF o de forma física te ubiques en la página 574 exactamente en los ejercicios propuestos de la sección 8.7, el ejercicio que vamos a realizar es el ejercicio # 5, que dice así:
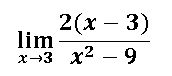
Como podemos ver el límite que vamos a resolver por la regla de l'hopital es un límite algebraico, el procedimiento para aplicar la regla de L'hopital consiste en derivar para este caso numerador y denominador de la función racional, esto es las veces que sea necesario hasta que se termine la indeterminación, sin embargo antes de empezar a resolver el límite es conveniente que revisemos si realmente el límite nos da de la forma indeterminada 0/0.
Lo primero que vamos a hacer es sustituir en donde está la variable x es hacia donde tiende el límite que are este caso es 3:
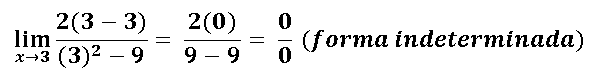
Como se puede observar en la imagen anterior, cuando se sustituye el 3 en la variable x nos da como resultado un límite de la forma indeterminada de la forma 0/0.
Para romper con esa indeterminación entonces aplicamos la regla de L'hopital, que nos dice que debemos de derivar numerador y denominador las veces que haga falta hasta que rompamos con esa indeterminación:
La derivada del numerador es la siguiente:
- Si realizamos la propiedad distributiva de la multiplicación antes de derivar nos queda:
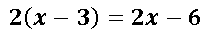
Finalmente si derivamos 2x-6 (que es el numerador nos quedaría de la siguiente manera:
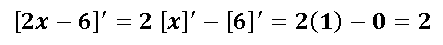
La derivada del numerador nos dio igual a 2.
Ahora vamos a resolver la derivada del denominador:
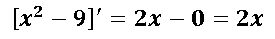
Una vez que hayamos encontrado la derivada del numerador y denominador de forma independiente, simplemente sustituimos esas derivada en el límite de la función racional y aplicamos límite para ver si la indeterminación de la forma 0/0 queda disuelta:
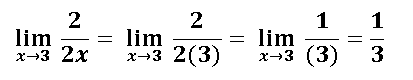
Exactamente queda evidenciado que aplicando la regla de L'hopital podemos resolver un límite algebraico de la forma indeterminado 0/0, e incluso si queremos aplicar otros métodos se puede ver como este límite también se puede resolver aplicando el método de factorización, para ello factorizamos el denominador:
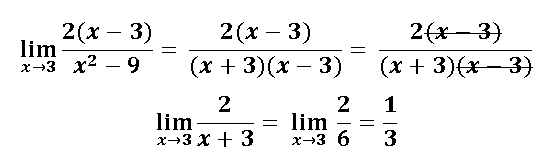
No en todas las circunstancias podemos tener un límite de la forma indeterminado 0/0 que podamos aplicar la factorización, ya que existen funciones trascendentales como las exponenciales y logarítmicas que no se pueden factorizar, por lo que resulta muy conveniente aplicar la regla de L'hopital.
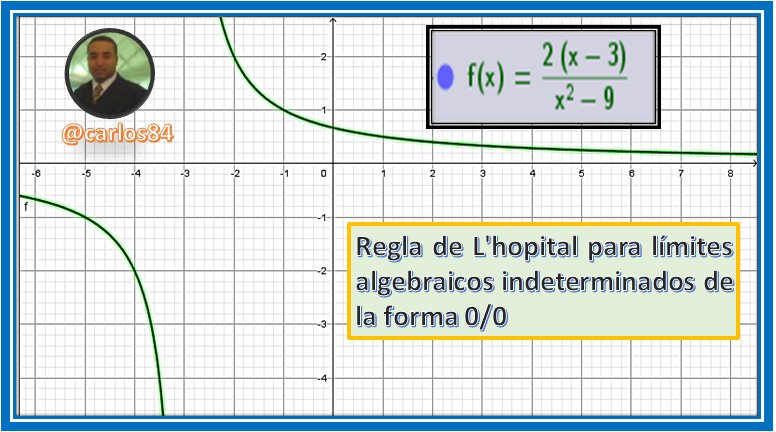
La conclusión del caso es que si logramos graficar dicha función nos diéramos cuenta que cuando la x se aproxima a 3 por derecha como por izquierda el valor de la imagen de la función es igual a 1/3.
Eso lo podemos ver evidenciado en el gráfico de esta función algebraica que voy a graficar empleando el software geogebra 5.0:
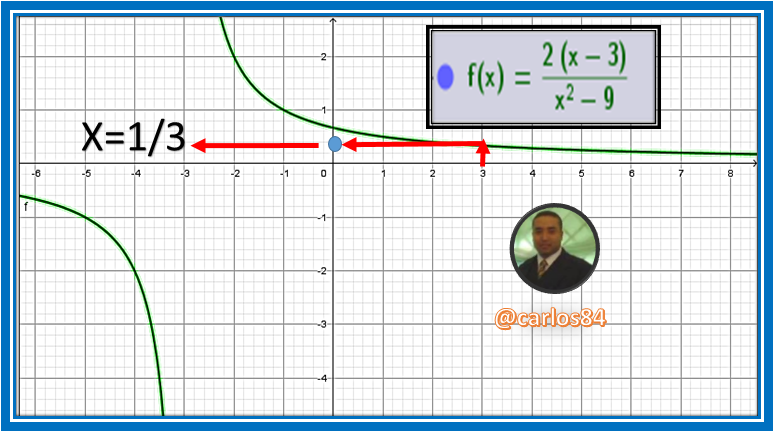
Precisamente cuando x se aproxima a 3 tanto por derecha como por izquierda la imagen de la función es igual a 1/3, con esto queda demostrado que este límite se puede resolver tanto por la regla de L'hopital, aplicando la regla de factorización y por análisis gráfico.
Me gustaría saber tus opiniones y que te pareció esta forma de abordar este límite de la forma indeterminado 0/0, cualquier duda me la puedes hacer saber en los comentarios, hasta una próxima entrega se despide tu amigo @carlos84.
Observaciones
Todas las ecuaciones las realice usando las herramientas de inserción de ecuaciones de Microsoft Word.
Para las imágenes de este post emplee el software geogebra y la edición empleando Microsoft Power Point.
Todas las imágenes son de mi autoría.
Referencia consultada y recomendada
Cálculo (completo) Vol 1 y 2 9na Edición Ron Larson & Bruce H. Edwards
https://twitter.com/CARLOSJB84/status/1363350372371353600
Su post ha sido valorado por @ramonycajal
Gracias por el apoyo a @ramonycajal y a cervantes. Saludos
Congratulations @carlos84! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
Your next target is to reach 170000 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out the last post from @hivebuzz:
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Gracias por el apoyo. Saludos
L'hopital fue mi gran dolor de cabeza en la universidad, al igual que las integrales dobles y triples,me costo mucho la comprensión de esos contenidos... Leyendo tu post estoy recordando y refrescando conocimientos, gracias por compartirlo
Hola @hannymarchan.
Creo que en cualquier momento inició una serie temática de integrales dobles y triples, sobre todo las dobles con las que se puede calcular el área de intersección entre dos curvas.
Recuerdo cuando vi calculo 1 odie los límites como no tienes idea jajaja fueron muchos trasnochos para poder pasar el parcial
Hola tocayo.
Realmente creo que todos pasamos por esa tortura, sin embargo deje de ver el cálculo como una tortura desde que empece a estudiar del libro de Larson, a partir de allí empecé a entender muchas cosas que a los profesores no le entendía. Uno casi nunca le gusta algo que no entiende, por eso tuve que entender los principios básicos para entender a profundidad el cálculo y que a la final me terminara gustando, hasta el punto de dar clases en eso.
Saludos Carlos y muy motivador para mi que hayas comentado mi post hermano, bendiciones para ti y tu familia.