Cálculo de área con integrales dobles
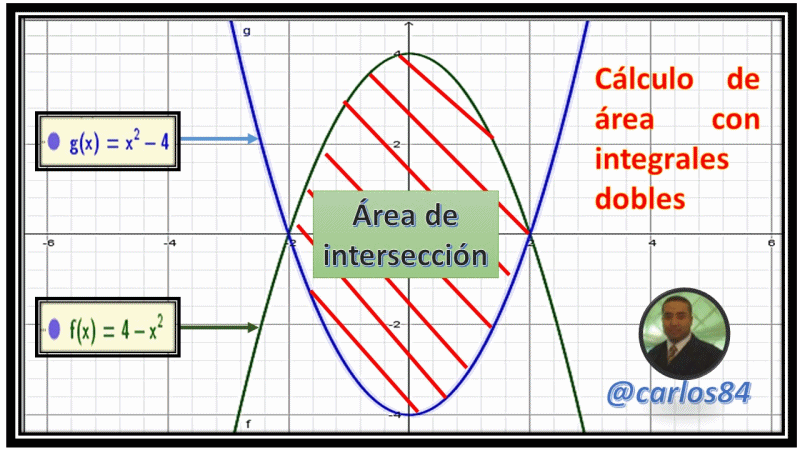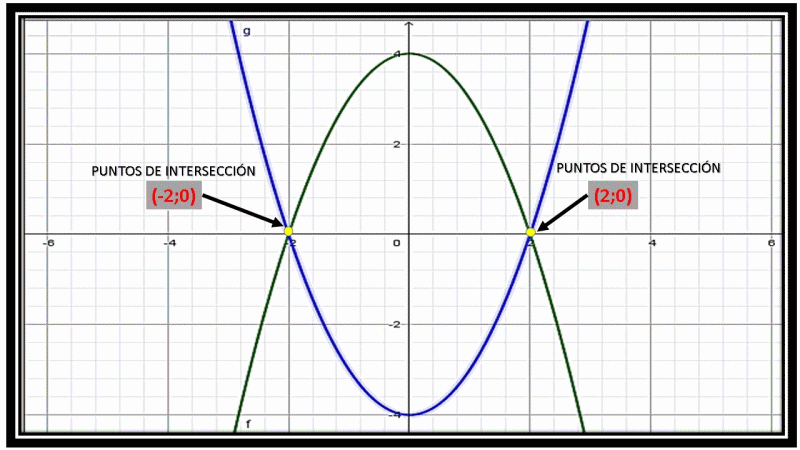
En base a un comentario que me dejó en uno de mis últimos post la compañera y amiga @hannymarchan sobre lo que hice recordar en sus años de universitaria acerca de las integrales dobles y triples, quise preparar este post referido al cálculo de áreas con integrales dobles.
El ejercicio es fácil y sencillo si tenemos en cuenta que hoy en día nos podemos apoyar en el uso de la tecnología y los software de uso libre, tal es el caso del software geogebra, el cual he utilizado para graficar la región limitada por dos funciones parabólicas, el ejercicio que quiero colocar como ejemplo para calcular el área entre dos curvas dice así:
Calcular el área de intersección entre dos parábolas mediante integrales dobles, las funciones se describen a continuación:
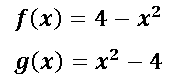
La región de intersección que limitan estas dos parábolas las pueden apreciar en la imagen que les muestro a continuación:
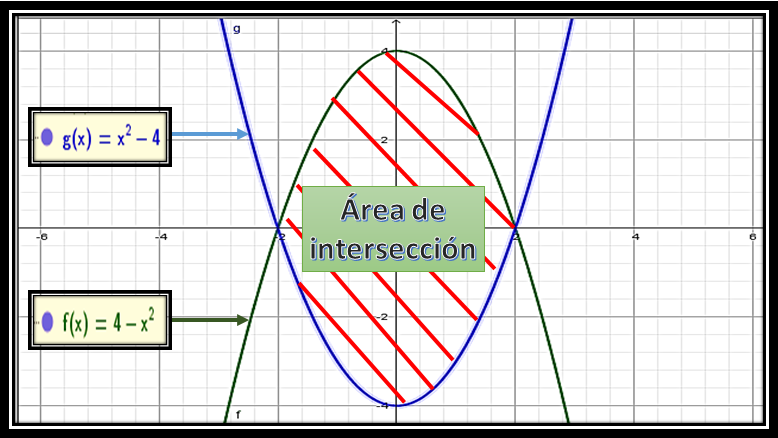
Como se puede apreciar en la imagen anterior las dos parábolas se interceptan generando un área de intersección que se puede calcular con integrales dobles.
Del área de intersección la curva que está por encima es f(x) y la que está por debajo es g(x). Para saber las coordenadas de los puntos de intersección les presento esta otra imagen:
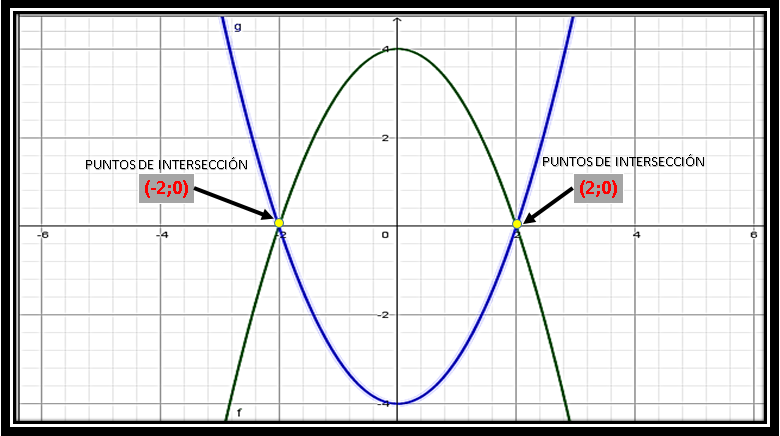
Como la región limitada por la intersección de las dos curvas es simétrica con respecto al eje Y, simplemente podemos calcular el área de dicha región en el intervalo de [0;2] y el resultado que nos dé lo multiplicamos por 2.
La fórmula que vamos aplicar para encontrar el área de intersección por medio de integrales dobles es la siguiente:
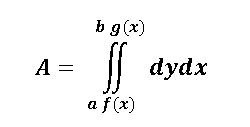
Como sabemos por principios básicos, el área de un rectángulo es base por altura, en este caso la intersección de las dos curvas genera una región limitada que no es un rectángulo, sin embargo podemos aplicar ese principio, por lo que la base puede ser la distancia que existe de cero a dos, y la altura es la distancia existente entre g(x) y f(x), es por ello que para el caso de los límites de integración a=0 y b= 2 y en el caso de las funciones f(x) y g(x) son las que se aprecian en el gráfico, por lo que el planteamiento de la integral que voy a resolver queda planteada de la siguiente manera:
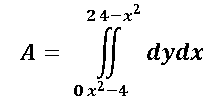
Para resolver esta integral doble, simplemente integramos el diferencial de y, como sabemos la integral del diferencial de una variable es la variable como tal, por lo que quedaría de la siguiente manera:
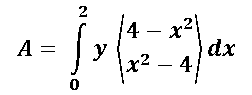
En el siguiente paso vamos a aplicar el teorema fundamental del cálculo, es decir en donde está la variable (y) vamos a sustituir el límite superior menos el límite superior, lo cual nos quedaría de la siguiente manera:
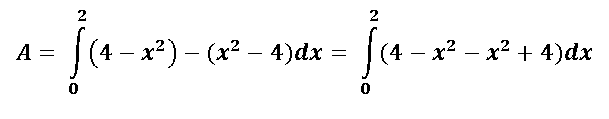
Cuando se realiza la sustitución del límite superior y del inferior y se multiplican los signos, finalmente nos queda la siguiente expresión:
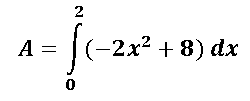
Ya para resolver la integral definida que se mostró simplemente integramos como si fuera una integral sencilla y aplicamos el teorema fundamental del cálculo para integrales definidas:
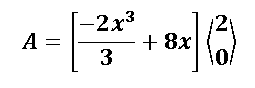
Tal y como se mostró, ya se resolvió la integral indefinida, solo falta aplicar el teorema fundamental del cálculo para terminar de saber el área de la mitad de la región limitada por la intersección de las dos curvas:
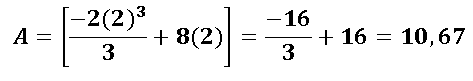
Como se pudo observar no se sustituyó el cero como límite inferior, ya que de igual manera entonces había que restarle cero, de manera tal que la mitad del área de la región limitada por la intersección de las dos curvas es 10,67 unidades de área, pero como necesitamos calcular toda el área completa multiplicamos este resultado por 2, lo que implica que el área de la región limitada por la intersección de las dos parábolas es:
A = 21,34 unidades de área
Observaciones
Las imágenes de los gráficos mostrados en este post son de mi autoría y fueron elaborados utilizando el software geogebra 5.0 y las herramientas de diseño de Microsoft Power Point.
Todas las ecuaciones fueron elaboradas utilizando las herramientas de inserción de ecuaciones de Microsoft Word.
Referencia recomendada
Cálculo (completo) Vol 1 y 2 9na Edición Ron Larson & Bruce H. Edwards
Su post ha sido valorado por @ramonycajal
Gracias por el apoyo a @ramonycajal y cervantes. Saludos
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app app and including @stemsocial as a beneficiary to get a stronger support.
Gracias por el apoyo. Saludos
como olvidar precisamente este problema donde el area a calcular tiene forma de huevo jajajaja... Gracias por compartir este contenido @carlos84
Jejejejeje, claro así es la intersección de dos parábolas, una que abre hacia arriba y la otra que abre hacia abajo, la intersección genera una región que tiene forma de un huevo, así mismo es amiga. Gracias por el comentario. Saludos.