Un Universo con Forma de Donut / A Universe Shaped Like Donut
Fuente / Source

Español

Un Universo con Forma de Donut
Algo que parecería salido de la imaginación de Homero Simpson, es a lo que apuntan nuevas observaciones sobre la forma que a gran escala tendría nuestro universo, según investigadores de la universidad de Lyon.
Una de las grandes incógnitas a resolver por la astrofísica es la forma que tendría nuestro universo, esta duda no se referiría en si a la forma desde un punto de vista práctico como lo concebimos cuando nos referimos a la forma de un objeto puntual, como un libro, un balón o una mesa. En el caso del universo este concepto se formula desde un punto de vista de su curvatura y topológica, a pequeña y gran escala, respectivamente. [1][4]
A pequeña escala o escala local, el concepto de forma se referiría a la curvatura del universo observable, que se puede definir como la curvatura generada por cualquier punto del espacio visible, del cual, el Fondo Cósmico de Microondas (acrónimo en inglés CMB) ha probado que tiene una estructura bastante homogénea e isotrópica, además de estarse expandiendo aceleradamente. Estas características, conducen a interpretar una geometría o curvatura constante, bajo la cual y como resultado de la teoría de la relatividad y la métrica de Friedmann-Lemaitre-Robertson-Walker, se obtiene el parámetro de densidad Ω el cual permite estimar la curvatura del espacio.[1]
Ω es el resultado de dividir la densidad promedio de materia en el universo observable entre la energía necesaria para que el universo sea plano. En el caso de Ω=1 la geometría del espacio sería plana y para magnitudes cosmológicas el teorema de Pitágoras se cumpliría, sin embargo, en los casos de Ω<1 y Ω>1 las geometría o curvatura sería abierta o cerrada, respectivamente, y en ambos casos, el teorema de Pitágoras seria herrado en magnitudes cosmológicas. [1]
Consecuencia de estas tres posibles variantes de Ω, el universo observable, podría responder a tres geometrías o curvaturas que definirían su forma:
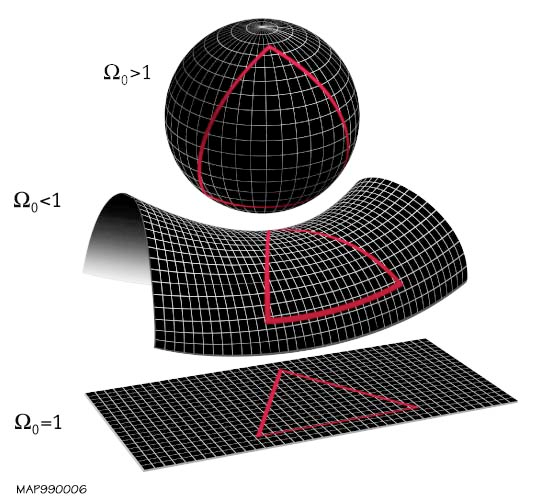
Gemetría local del universo Fuente
Geometría euclidiana de tres dimensiones, en la cual se cumpliría el teorema de Pitágoras y los ángulos internos de un triángulo de magnitudes cosmológicas siempre sumarían 180°, pues las líneas rectas se mantendrían siempre recta. [1][4]
Geometría esférica en tres dimensiones, en la cual el teorema de Pitágoras no se cumpliría pues los ángulos internos de un triángulo de magnitud cosmológica sumarían más de 180°, pues las rectas que formas sus lados se curvarían hacia afuera. [1][4]
Geometría hiperbólica en tres dimensiones, en la cual no se cumpliría el teorema de Pitágoras, pues los ángulos internos de un triángulo de magnitud cosmológica sumarían menos de 180°, al curvarse hacia adentro las rectas que forman sus lados. [1][4]
Desde el punto de vista de la forma global del universo, esta incluiría la de la partes observables y no observables de él. En general, en la forma global del universo se extiende la magnitud de la forma local, cobrando importancia su compacidad y si la conexión de sus puntos es simple o no-simple.
En consecuencia, de esto se deducen tres formas globales básicas para el universo:
Universo plano: en un universo plano, las geometrías locales también son planas, además del espacio euclídeo existen otras geometrías en las que esto es posible, lo que incluye al cilindro, el toro y la cinta de Möbius. En un universo plano, la topología puede ser o no compacta y finita. En el caso de un espacio euclídeo, cualquier línea recta proyectada desde un punto se prolongaría por siempre por lo que se trataría de un espacio infinito. Sin embargo, esto no ocurriría en geometrías como el cilindro o el toro, donde estas líneas podrían recorrer diferentes caminos en los que podrían llegar a cerrarse sobre si mismas o a sobreponerse, por lo que serían espacio compactos o finitos. [1][4]
Universo esférico: en un universo esférico las geometrías locales podrían aparecer como planas o curvas, dependiendo de la magnitud del universo observable. De ser la geometría local curva, podría deducirse una curvatura global pequeña, esto conduciría a la determinación de un espacio de forma esférica, en consecuencia, con una topología compacta, limitada. En este tipo de universo cualquier línea recta trazada partir de un punto podría llegar nuevamente a su punto de origen. [1][4]
Universo hiperbólico: un universo hiperbólico podría definirse como con la forma de una silla de montar, en el las geometrías locales podrían ser tanto planas como curvadas, dependiendo no sólo de la magnitud, sino de la ubicación del universo observable. En este tipo de universos las líneas rectas pueden proyectarse hasta el infinito, pudiendo llegar a sobre ponerse, pero sin regresar nunca a su origen, en consecuencia, se trataría de un espacio infinito. [1][4]
Un aspecto importante que puede deducirse de la forma del universo es que dependiendo de la cantidad de energía oscura que este podría tener diferentes fines, dada su característica de encontrarse en un estado de expansión acelerada. Así, si el universo fuese plano o hiperbólico, dependiendo de la cantidad de energía oscura que en el exista, su fin podría darse en un gran congelamiento, con un universo carente de materia y radiación en el que las temperaturas poco a poco llegarían a ser iguales al cero absoluto; o en un gran desgarramiento, en el cual la energía oscura llegaría a superar incluso a la fuerza nuclear fuerte, desgarrando la materia a niveles atómicos. Mientras que si el universo fuese esférico su final estaría dado por una gran colisión, en la que la expansión llegaría a un punto en la que se revertiría llevando al universo a ser comprimido como un todo en una singularidad similar a la del big-bang. [1]
Hasta la fecha las evidencias proporcionadas por el estudio de las supernovas lejanas y del fondo cósmico de microondas, parecen dar prueba de un universo plano e infinito, sin embargo resientes trabajos, dados a conocer por el astrofísico Thomas Buchert de la universidad de Lyon, parecen llevar a la conclusión de que el universo podría no ser infinito y estar cerrado sobre si mismo con múltiples conexiones, por lo que tendría una forma de donut o toro en tres dimensiones, lo cual, aunque correspondería aún a una geometría plana, a diferencia de la euclidiana, seria finita o compacta. [2][3]
Como consecuencia de esto, podríamos partir de un punto y viajando en línea recta, eventualmente regresar al punto de partida, con lo que podríamos determinar el tamaño exacto del mismo, sin embargo, esto no sería posible debido a la expansión del espacio, que sería superior a la velocidad de la luz, por lo que en viaje se prolongaría por siempre. [2][3]
Para llegar a esta hipótesis, Buchert y sus colegas, estudiaron las diferencias de temperatura que se presentan en el CMB, manifestadas como interrupciones en su homogeneidad o anisotropías, buscando replicar su distribución, a través de la simulación, partiendo de diferentes geometrías para el universo actual, llegando a resultados que les permitieron concluir, que para obtener tal configuración del CMB, el universo debe ser finito y cerrarse sobre si mismo, lo que aunado a las observaciones de la geometría local, conduce a especular que su forma puede ser similar a la de un donut o toro en tres dimensiones, y que su tamaño total, sería menor que el estimado, pudiendo ser de unas cuatro veces el universo observable. [2][3]
Buchest también aclara que estos resultados son preliminares y requieren más evidencia, pues pueden ser explicados por efectos, atribuibles a los instrumentos usados en las mediciones.
Una consecuencia directa de un universo compacto en forma de toro o donut y cuyas dimensiones fueran las previstas por Buchest y su equipo, seria la de un final en forma de gran colapso o choque, al igual que en un universo esférico, pero dado las dimensiones previstas, este podría suceder mucho antes de los sugerido para una geometría esférica.

English

A Universe Shaped Like Donut
Something that would seem to come out of the imagination of Homer Simpson, is what new observations point to on the form that on great scale would have our universe, according to investigators of the university of Lyon.
One of the great unknowns to solve by the astrophysics is the form that would have our universe, this doubt would not refer in if to the form from a practical point of view as we conceive it when we refer to the form of a punctual object, like a book, a ball or a table. In the case of the universe this concept is formulated from a point of view of its curvature and topology, on a small and large scale, respectively. [1][4]
On a small or local scale, the concept of shape would refer to the curvature of the observable universe, which can be defined as the curvature generated by any point in visible space, of which the Cosmic Microwave Background (CMB) has proven to have a fairly homogeneous and isotropic structure, as well as to be expanding rapidly. These characteristics, lead to interpret a constant geometry or curvature, under which and as a result of the theory of relativity and the Friedmann-Lemaitre-Robertson-Walker metric, the density parameter Ω is obtained, which allows estimating the curvature of space.[1] Ω is the result of dividing the density parameter Ω into two parts.
Ω is the result of dividing the average density of matter in the observable universe by the energy required for the universe to be flat. In the case of Ω=1 the geometry of space would be flat and for cosmological magnitudes the Pythagorean theorem would be fulfilled, however, in the cases of Ω<1 and Ω>1 the geometry or curvature would be open or closed, respectively, and in both cases, the Pythagorean theorem would be wrong in cosmological magnitudes. [1]
Consequence of these three possible variants of Ω, the observable universe, could respond to three geometries or curvatures that would define its shape:

Local gemmetry of the universe. Source
Euclidean geometry of three dimensions, in which the Pythagorean theorem would be fulfilled and the internal angles of a triangle of cosmological magnitudes would always add up to 180°, since the straight lines would always remain straight. [1][4]
Spherical geometry in three dimensions, in which the Pythagorean theorem would not be fulfilled because the internal angles of a triangle of cosmological magnitude would add up to more than 180°, since the straight lines that form its sides would curve outward. [1][4]
Hyperbolic geometry in three dimensions, in which the Pythagorean theorem would not be fulfilled, since the internal angles of a triangle of cosmological magnitude would add up to less than 180°, since the straight lines that form its sides would curve inward. [1][4]
From the point of view of the overall shape of the universe, this would include that of the observable and unobservable parts of it. In general, in the global form of the universe extends the magnitude of the local form, gaining importance its compactness and whether the connection of its points is simple or non-simple.
Consequently, three basic global forms for the universe can be deduced from this:
Flat universe: in a flat universe, the local geometries are also flat, in addition to Euclidean space there are other geometries in which this is possible, which includes the cylinder, the torus and the Möbius ribbon. In a flat universe, the topology may or may not be compact and finite. In the case of a Euclidean space, any straight line projected from a point would extend forever so it would be an infinite space. However, this would not occur in geometries such as the cylinder or the torus, where these lines could travel different paths in which they could close on themselves or overlap, so they would be compact or finite space. [1][4]
Spherical universe: in a spherical universe the local geometries could appear as flat or curved, depending on the magnitude of the observable universe. If the local geometry is curved, a small global curvature could be deduced, this would lead to the determination of a spherical shaped space, consequently, with a compact, limited topology. In this type of universe any straight line drawn from a point could arrive again at its point of origin. [1][4]
Hyperbolic universe: a hyperbolic universe could be defined as having the shape of a saddle, in which the local geometries could be either flat or curved, depending not only on the magnitude but also on the location of the observable universe. In this type of universes the straight lines can be projected to infinity, being able to overlap, but without ever returning to its origin, consequently, it would be an infinite space. [1][4]
An important aspect that can be deduced from the form of the universe is that depending on the amount of dark energy that this could have different ends, given its characteristic of being in a state of accelerated expansion. Thus, if the universe were flat or hyperbolic, depending on the amount of dark energy that exists in it, its end could occur in a great freezing, with a universe devoid of matter and radiation in which the temperatures would gradually become equal to absolute zero; or in a great tearing, in which the dark energy would overcome even the strong nuclear force, tearing the matter to atomic levels. Whereas if the universe were spherical its end would be given by a great collision, in which the expansion would reach a point where it would be reversed leading the universe to be compressed as a whole in a singularity similar to that of the big-bang [1].
To date the evidence provided by the study of distant supernovae and the cosmic microwave background, seem to give evidence of a flat and infinite universe, however recent work, released by the astrophysicist Thomas Buchert of the University of Lyon, seem to lead to the conclusion that the universe might not be infinite and be closed on itself with multiple connections, so it would have a donut or torus shape in three dimensions, which, although it would still correspond to a flat geometry, unlike the Euclidean, would be finite or compact. [2][3]
As a consequence of this, we could start from a point and traveling in a straight line, eventually return to the starting point, with which we could determine the exact size of the same, however, this would not be possible due to the expansion of space, which would be greater than the speed of light, so that the trip would be prolonged forever. [2][3]
To arrive at this hypothesis, Buchert and his colleagues, studied the temperature differences that occur in the CMB, manifested as interruptions in its homogeneity or anisotropies, seeking to replicate its distribution, through simulation, starting from different geometries for the current universe, reaching results that allowed them to conclude, that to obtain such a configuration of the CMB, the universe must be finite and closed on itself, which together with the observations of the local geometry, leads to speculate that its shape may be similar to that of a donut or torus in three dimensions, and that its total size would be smaller than the estimated, and could be about four times the observable universe. [2][3]
Buchest also clarifies that these results are preliminary and require further evidence, as they may be explained by effects attributable to the instruments used in the measurements.
A direct consequence of a compact universe in the shape of a torus or donut, and whose dimensions were those predicted by Buchest and his team, would be that of an end in the form of a large collapse or shock, as in a spherical universe, but given the predicted dimensions, this could happen much earlier than suggested for a spherical geometry.

Referencias / Sources
[1] Wikipedia. Forma del universo. Wikipedia.
[2] Romero, Sarah. El universo podría tener la forma de un dónut. Muy Interesante
[3] DW. Astrofísicos dicen que el universo podría ser en realidad un gigantesco donut en 3D. DW
[4] Rivero, Alex. ¿Qué forma tiene el universo?. Astrobitácora.
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.
Su post ha sido valorado por @goya
Yay! 🤗
Your content has been boosted with Ecency Points, by @francyrios75.
Use Ecency daily to boost your growth on platform!
Support Ecency
Vote for new Proposal
Delegate HP and earn more