Vectors and the Geometry of Space: Vectors

avatar
(Edited)

In this video I go over the second section in my Vectors and the Geometry of Space calculus book chapter and this time go over Vectors. Vectors are mathematical objects that describe both magnitude and direction. These are very useful in physics and science in general as it can simplify the mathematical description of 3D-dimensional space. I go over an introduction on Vectors as well as their properties and corresponding vector algebra.

The topics covered as well as their timestamps are listed below.

  • Introduction: 0:00
  • Sections in Calculus Book Chapter: 0:58
  • Topics to Cover: 2:16
  1. Vectors: 3:01
  2. Combining Vectors: 5:46
    • Definition of Vector Addition: 7:03
      • Triangle Law: 7:54
      • Parallelogram Law: 8:40
    • Example 1: 11:21
    • Definition of Scalar Multiplication: 14:50
    • Example 2: 21:01
  3. Components: 22:27
    • Equation 1: 35:36
    • Example 3: 36:11
    • Magnitude or Length of a Vector: 37:48
    • Vector Algebra: 39:42
    • Example 4: 50:08
    • Note on n-Dimensional Vectors: 56:31
    • Properties of Vectors: 58:57
    • Standard Basis Vectors: 1:08:20
    • Example 5: 1:20:56
    • Historical Note: 1:25:04
    • Unit Vectors: 1:27:15
    • Example 6: 1:31:44
  4. Applications: 1:35:00
    • Example 7: 1:35:45

Watch video on:

Download video notes: https://1drv.ms/b/s!As32ynv0LoaIiZ8ud7u3FkR_HvBmTQ?e=zaylf8

View video sections playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0EiRECLVkBCcFhSpbSz8XIw

View the full Vectors and Geometry of Space video series: https://www.youtube.com/playlist?list=PLai3U8-WIK0FjJpwnxwdrOR7L8Ul8VZoZ

View Video Notes Below!

Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate
Buy MES merchandise! https://mes.fm/store
More links: https://linktr.ee/matheasy
Follow my research in real-time on my MES Links Telegram: https://t.me/meslinks
Subscribe to MES Truth: https://mes.fm/truth

Reuse of my videos:

  • Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.

Fight back against censorship:

  • Bookmark sites/channels/accounts and check periodically
  • Remember to always archive website pages in case they get deleted/changed.

Recommended Books:

Join my forums!

Follow along my epic video series:

NOTE #1: If you don't have time to watch this whole video:

Browser extension recommendations:

Vectors and the Geometry of Space: Vectors

Calculus Book Reference

Note that I mainly follow along the following calculus book:

  • Calculus: Early Transcendentals 7th Edition by James Stewart
  • Note: In the earlier videos I used the 6th edition.

Sections in Calculus Book Chapter

I have made a list of the sections in this particular chapter with links to the Hive post of the videos I have already finished.

Vectors and the Geometry of Space

  1. 3-D Coordinate Systems
  2. Vectors (Current Video)
  3. The Dot Product
  4. The Cross Product
    • Discovery Project: The Geometry of a Tetrahedron
  5. Equations of Lines and Planes
    • Laboratory Project: Putting 3D in Perspective
  6. Cylinders and Quadric Surfaces
  7. Review
    • True-False Quiz
  8. Problems Plus

Topics to Cover

Note that timestamps will be included in the video description for each topic listed below.

  1. Vectors
  2. Combining Vectors
    • Definition of Vector Addition
      • Triangle Law
      • Parallelogram Law
    • Example 1
    • Definition of Scalar Multiplication
    • Example 2
  3. Components
    • Equation 1
    • Example 3
    • Magnitude or Length of a Vector
    • Vector Algebra
    • Example 4
    • Note on n-Dimensional Vectors
    • Properties of Vectors
    • Standard Basis Vectors
    • Example 5
    • Historical Note
    • Unit Vectors
    • Example 6
  4. Applications
    • Example 7

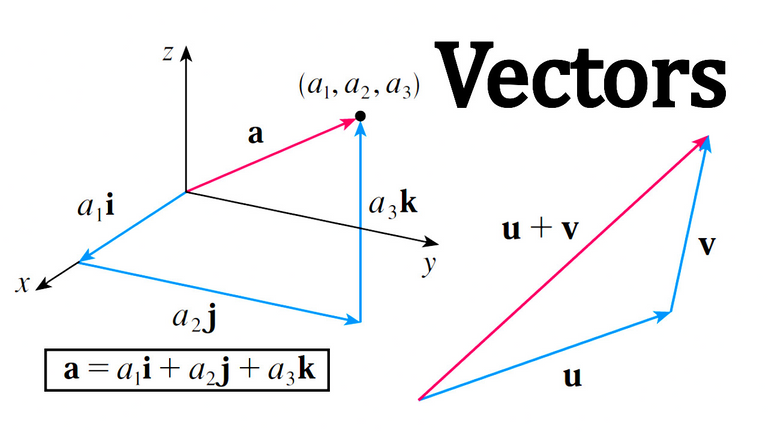
Vectors

The term vector is used by scientists to indicate a quantity (such as displacement or velocity or force) that has both magnitude and direction.

A vector is often represented by an arrow or a directed line segment.

The length of the arrow represents the magnitude of the vector and the arrow points in the direction of the vector.

We denote a vector by printing a letter in boldface (v) or by putting an arrow above the letter image.png.

MES Note: In my earlier videos I would bold every equation or symbol since there were no vectors involved. For this video I will only bold vectors.

Hive Note: Note that the current websites that I use to post on the Hive blockchain don't have the ability, that I know of at least, to post symbols with arrows on top such as vectors. Thus, I will resort to pasting images instead.

For instance, suppose a particle moves along a line segment from point A to point B.

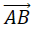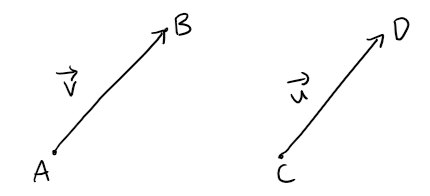
The corresponding displacement vector v, shown in the figure below, has initial point A (the tail) and terminal point B (the tip) and we indicate this by writing v = image.png.

image.png

Notice that the vector

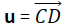
image.png

has the same length and the same direction as v even though it is in a different position.

We say that u and v are equivalent (or equal) and we write u = v.

The zero vector, denoted by 0, has length 0.

It is the only vector with no specific direction.

Combining Vectors

Suppose a particle moves from A to B, so its displacement is

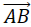
image.png

Then the particle changes direction and moves from B to C, with displacement vector

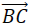
image.png

as in the figure below.

image.png

The combined effect of these displacements is that the particle has moved from A to C.

The resulting displacement vector

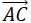
image.png

is called the sum of image.png and we write:

image.png

In general, if we start with vectors u and v, we first move v so that its tail coincides with the tip of u and define the sum of u and v as follows.

Definition of Vector Addition

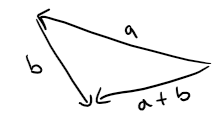
If u and v are vectors positioned so the initial point of v is at the terminal point of u, then the sum u + v is the vector from the initial point of u to the terminal point of v.

Triangle Law

The definition of vector addition is illustrated in the figure below.

image.png

You can see why this definition is sometimes called the Triangle Law.

Parallelogram Law

In the figure below, we start with the same vectors u and v as in the above figure and draw another copy of v with the same initial point as u.

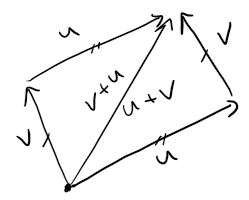
image.png

Completing the parallelogram, we see that u + v = v + u.

This also gives another way to construct the sum:

If we place u and v so they start at the same point, then u + v lies along the diagonal of the parallelogram with u and v as sides.

This is called the Parallelogram Law.

Note that a parallelogram is quadrilateral (4-sided polygon) with parallel opposite sides.

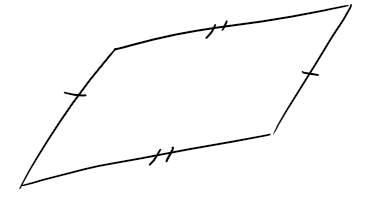
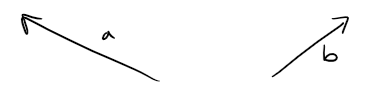
image.png

Example 1

Draw the sum of the vectors a and b shown in the figure below.

image.png

Solution:

First we translate b and place its tail at the tip of a, being careful to draw a copy of b that has the same length and direction.

Then we draw the vector a + b starting at the initial point of a and ending at the terminal point of the copy of b.

image.png

Alternatively, we could place b so it starts where a starts and construct a + b by the Parallelogram Law.

image.png

It is possible to multiply a vector by a real number c.

In this context we call the real number c a scalar to distinguish it from a vector.

For instance, we want 2v to be the same vector as v + v, which has the same direction v but is twice as long.

In general, we multiply a vector by a scalar as follows.

Definition of Scalar Multiplication

If c is a scalar and v is a vector, then the scalar multiple cv is the vector whose length is |c| times the length of v and whose direction is the same as v if c > 0 and is opposite to v if c < 0.

If c = 0 or v = 0, then cv = 0.

This definition is illustrated in the figure below.

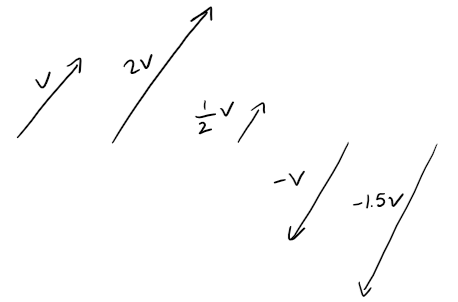
image.png

We see that real numbers work like scaling factors here; that's why we call them scalars.

Notice that two nonzero vectors are parallel if they are scalar multiples of one another.

In particular, the vector -v = (-1)v has the same length as v but points in the opposite direction.

We call it the negative of v.

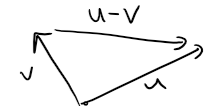
By the difference u - v of two vectors we mean:

u - v = u + (-v)

So we can construct u - v by first drawing the negative of v, -v, and then adding it to u by the Parallelogram Law as in the figure below.

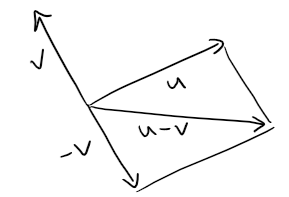
image.png

Alternatively, since v + (u - v) = u, the vector u - v, when added to v, gives u.

So we could construct u - v as in the figure below by means of the Triangle Law.

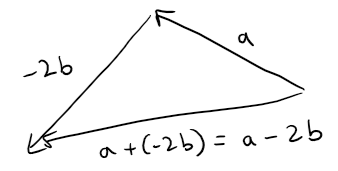
image.png

Example 2

If a and b are the vectors shown below, draw a - 2b.

image.png

Solution:

We first draw the vector -2b pointing in the direction opposite to b and twice as long.

We place it with its tail at the tip of a and then use the Triangle Law to draw a + (-2b) as in the figure below.

image.png

Components

For some purposes it's best to introduce a coordinate system and treat vectors algebraically.

If we place the initial point of a vector a at the origin of a rectangular coordinate system, then the terminal point of a has coordinates of the form (a1,a2) or (a1, a2, a3), depending on whether our coordinate system is two- or three-dimensional (see figure below).

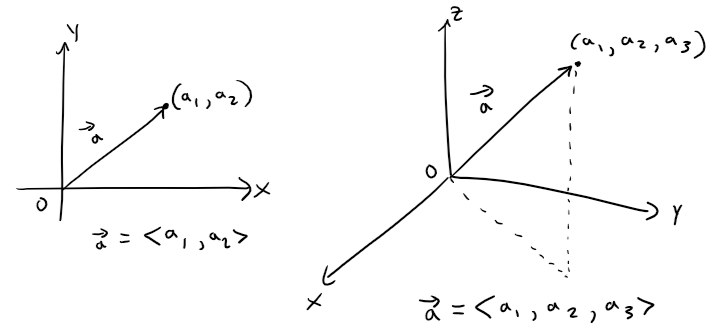
image.png

These coordinates are called the components of a and we write:

a = <a1, a2>

or

a = <a1, a2, a3>

We use the notation <a1, a2> for the ordered pair that refers to a vector so as not to confuse it with the ordered pair (a1, a2) that refers to a point in the plane.

For instance, the vectors in the figure below are all equivalent to the vector

image.png

whose terminal point is P(3, 2).

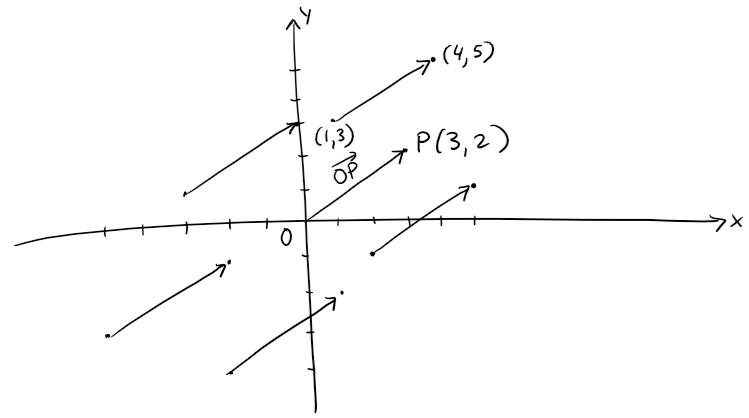
image.png

What they have in common is that the terminal point is reached from the initial point by a displacement of three units to the right and two upward.

We can think of all these geometric vectors as representations of the algebraic vector b = <3, 2>.

The particular representation 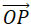image.png from the origin to the point P(3, 2) is called the position vector of the point P.

In three dimensions, the vector a = 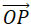image.png = <a1, a2, a3> is the position vector of the point P(a1, a2, a3) (see figure below).

image.png

Let's consider any other representation (AB) ⃗ of a, where the initial point is A(x1, y1, z1) and the terminal point is B(x2, y2, z2).

Then we must have:

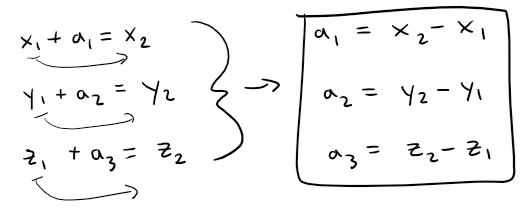
image.png

Thus we have the following result.

Equation 1

Given the points A(x1, y1, z1) and B(x2, y2, z2), the vector a with representation AB is:

a = <x2 - x1, y2 - y1, z2 - z1>

Example 3

Find the vector represented by the directed line segment with initial point A(2, -3, 4) and terminal point B(-2, 1, 1).

Solution:

By Equation 1, the vector corresponding to image.png is:

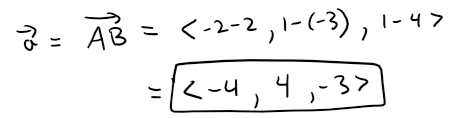
image.png

Magnitude or Length of a Vector

The magnitude or length of the vector v is the length of any of its representations and is denoted by the symbol |v| or ǁvǁ.

By using the distance formula to compute the length of a segment OP (from the first video in this chapter), we obtain the following formulas.

The length of the two-dimensional vector a = <a1, a2> is:

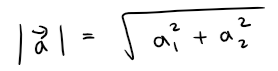
image.png

The length of the three-dimensional vector a = <a1, a2, a3> is:

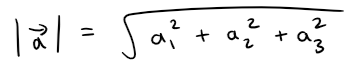
image.png

Vector Algebra

How do we add vectors algebraically?

The figure below shows that if a = <a1, a2> and b = <b1, b2>, then the sum is a + b = <a1 + b1, a2 + b2>, at least for the case where the components are positive.

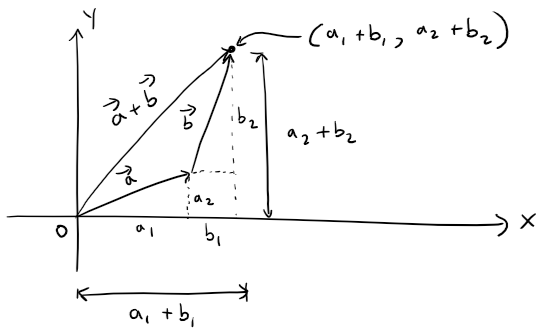
image.png

In other words, to add algebraic vectors we add their components.

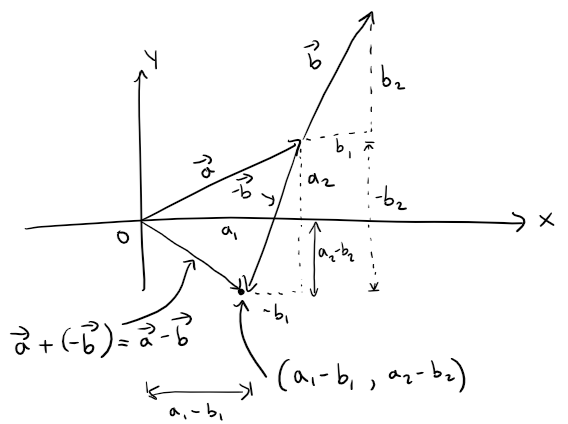
Similarly, to subtract vectors we subtract components.

image.png

From the similar triangles in the figure below, we see that the components of ca are ca1 and ca2.

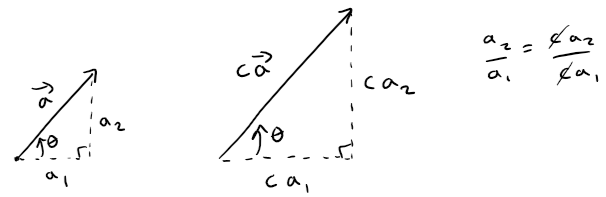
image.png

So to multiply a vector by a scalar we multiply each component by that scalar.

If a = <a1, a2> and b = <b1, b2>, then:

a + b = <a1 + b1, a2 + b2>
a - b = <a1 - b1, a2 - b2>
ca = <ca1, ca2>

Similarly for three-dimensional vectors:

<a1, a2, a3> + <b1, b2, b3> = <a1 + b1, a2 + b2, a3 + b3>
<a1, a2, a3> - <b1, b2, b3> = <a1 - b1, a2 - b2, a3 - b3>
c<a1, a2, a3> = <ca1, ca2, ca3>

Example 4

If a = <4, 0, 3> and b = <-2, 1, 5>, find |a| and the vectors a + b, a - b, 3b, and 2a + 5b.

Solution:

image.png

We denote by V2 the set of all two-dimensional vectors and by V3 the set of all three-dimensional vectors.

More generally, we will later need to consider the set Vn of all n-dimensional vectors.

An n-dimensional vector is an ordered n-tuple:

a = <a1, a2, … , an>

where a1, a2, … , an are real numbers that are called the components of a.

Addition and scalar multiplication are defined in terms of components just as for the case n = 2 and n = 3.

Note on n-Dimensional Vectors

Vectors in n dimensions are used to list various quantities in an organized way.

For instance the components of a six-dimensional vector:

p = <p1, p2, p3, p4, p5, p6>

might represent the prices of six different ingredients required to make a particular product.

Four-dimensional vectors <x, y, z, t> are used in relativity theory, where the first three components specify a position in space and the fourth represents time.

Properties of Vectors

If a, b, and c are vectors in Vn and c and d are scalars, then:

  1. a + b = b + a
  2. a + (b + c) = (a + b) + c
  3. a + 0 = a
  4. a + (-a) = 0
  5. c(a + b) = ca + cb
  6. (c + d)a = ca + da
  7. (cd)a = c(da)
  8. 1a = a

These eight properties of vectors can be readily verified either geometrically or algebraically.

For instance, Property 1 can be seen from the earlier figure for the Parallelogram Law or as follows for the case n = 2:

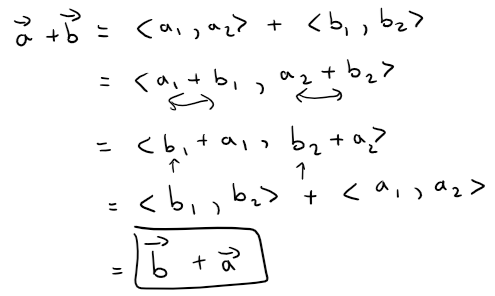
image.png

We can see why Property 2 (the associative law) is true by looking at the figure below and applying the Triangle Law several times:

The vector

image.png

is obtained either by first constructing a + b and then adding c or by adding a to the vector b + c.

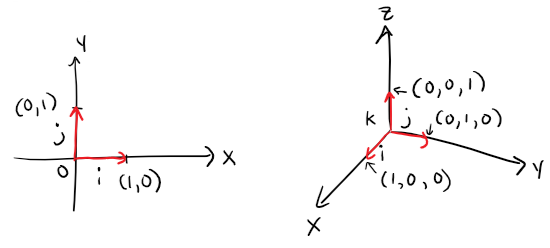
image.png

Standard Basis Vectors

Three vectors in V3 play a special role.

Let:

i = <1, 0, 0>
j = <0, 1, 0>
k = <0, 0, 1>

These vectors i, j, and k are called the standard basis vectors.

They have length 1 and point in the directions of the positive x-, y-, and z-axes.

Similarly, in two dimensions we define:

i = <1, 0>
j = <0, 1>

image.png

If a = <a1, a2, a3>, then we can write:

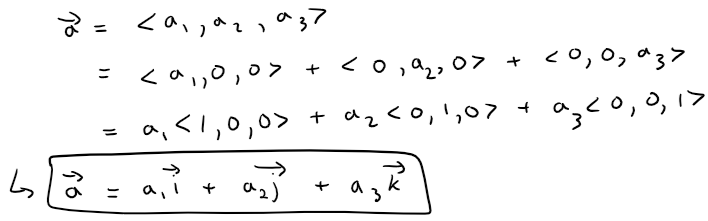
image.png

Thus any vector in V3 can be expressed in terms of i, j, and k.

For instance:

<1, -2, 6> = i - 2j + 6k

Similarly, in two dimensions, we can write:

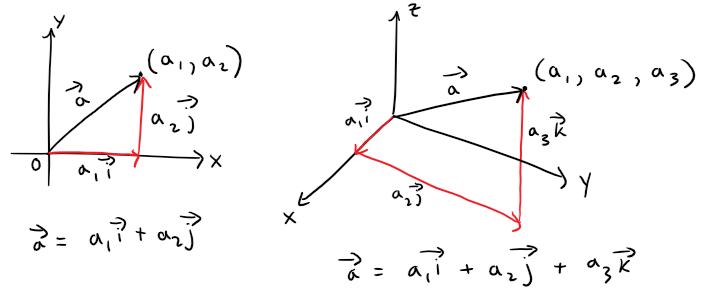
a = <a1, a2> = a1i + a2j

See the figure below for the geometric interpretation for the above equations and compare with the earlier figures for the standard basis vectors.

image.png

Example 5

If a = i + 2j - 3k and b = 4i + 7k, express the vector 2a + 3b in terms of i, j, and k.

Solution:

Using Properties 1, 2, 5, 6, and 7 of vectors, we have:

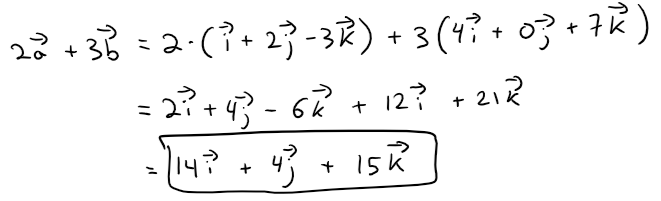
image.png

Historical Note

Josiah Willard Gibbs (11 February 1839 - 28 April 1903), a professor of mathematical physics at Yale College, published the first book on vectors, Vector Analysis, in 1881.

More complicated objects, called quaternions, had earlier been invented by William Rowan Hamilton ( 3/4 August 1805 - 2 September 1865) as mathematical tools for describing space, but they weren't easy for scientists to use.

Quaternions have a scalar part and a vector part, and are generally written in the form:

a + bi + cj + dk

where a, b, c, and d are real numbers; and i, j, and k are the basic quaternions.

Gibb's idea was to use the vector part separately.

James Clerk Maxwell (13 June 1831 - 5 November 1879) and Oliver Heaviside (18 May 1850 - 3 February 1925) had similar ideas, but Gibb's approach has proved to be the most convenient way to study space.

Unit Vectors

A unit vector is a vector whose length is 1.

For instance, i, j, and k are all unit vectors.

In general, if a ≠ 0, then the unit vector that has the same direction as a is:

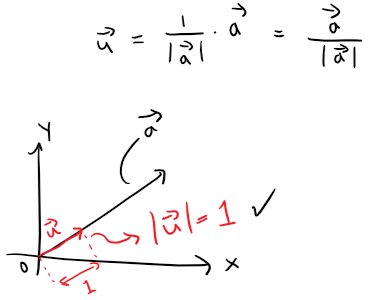
image.png

In order to verify this, we let c = 1/|a|.

Then u = ca and c is a positive scalar, so u has the same direction as a.

Also:

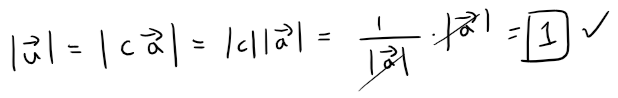
image.png

Example 6

Find the unit vector in the direction of the vector 2i - j - 2k.

Solution:

The given vector has length:

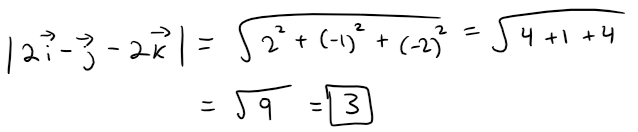
image.png

Thus, by the earlier equation for a unit vector, the unit vector with the same direction is:

image.png

Applications

Vectors are useful in many aspects of physics and engineering.

In future videos, we will see how they describe the velocity and acceleration of objects moving in space.

Here we look at forces.

A force is represented by a vector because it has both a magnitude (measured in pounds or newtons) and a direction.

If several forces are acting on an object, the resultant force experienced by the object is the vector sum of these forces.

Example 7

A 100-lb weight hangs from two wires as shown in the figure below.

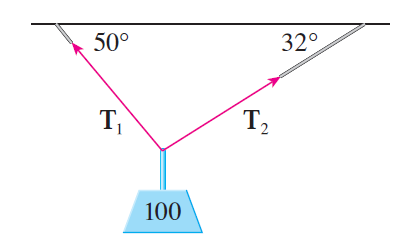
image.png

Find the tensions (forces) T1 and T2 in terms of their horizontal and vertical components.

Solution:

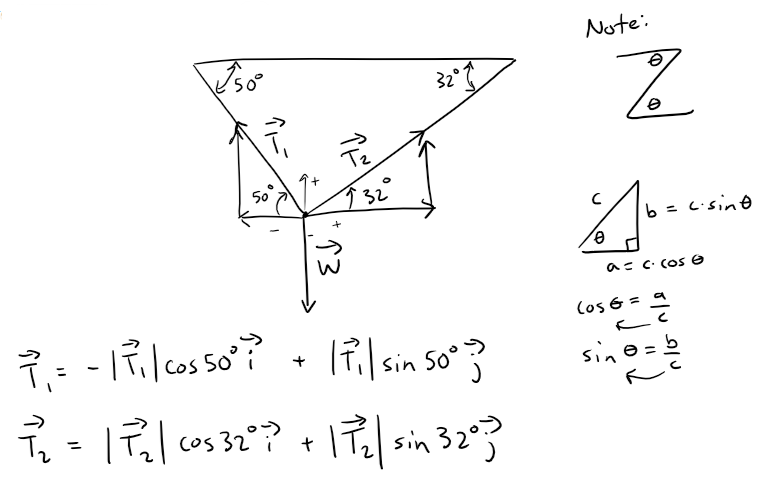
We first express T1 and T2 in terms of their horizontal and vertical components.

From the figure below, we see that:

image.png

The resultant T1 + T2 of the tensions counterbalances the weight w and we must have:

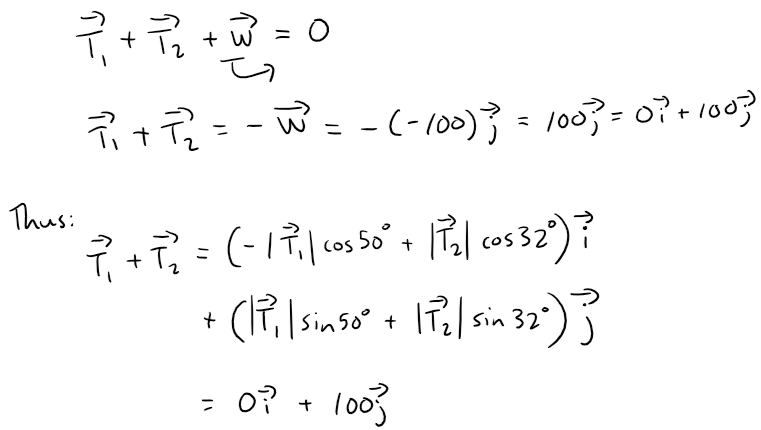
image.png

Equating components and solving for |T1| and |T2| we get the magnitudes of the tensions:

image.png

Calculation check:

|T1| = 100/(sin(50) + tan(32)*cos(50)) = 85.63823503206792 lb

|T2| = 85.63823503206792 * cos(50) / cos(32) = 64.91046515348027 lb

Substituting these values in the earlier vector representation, we obtain the tension vectors:

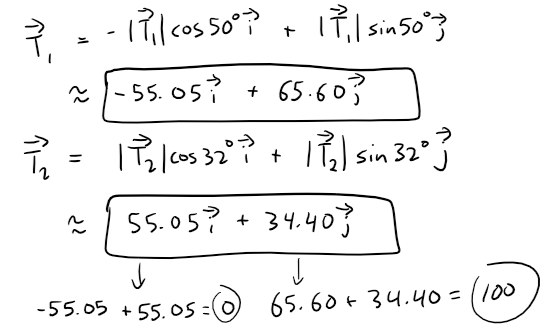
image.png

Calculation check:

-|T1|cos 50° = - 85.63823503206792 * cos(50) = -55.04719639403698
|T1|sin 50° = 85.63823503206792 * sin(50) = 65.6026940648326

|T2|cos 32° = 64.91046515348027 * cos(32) = 55.04719639403697
|T2|sin 32° = 64.91046515348027 * sin(32) = 34.39730593516734

-55.04719639403698 + 55.04719639403697 = -1.0E-14
65.6026940648326 + 34.39730593516734 = 99.99999999999994

mathematics calculus science stemgeeks palnet proofofbrain education math stem vectors
0
0
0.000
1 comments
avatar

Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!

Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).

You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support. 
 

0
0
0.000
Reply