Vectors and the Geometry of Space: 3D Coordinate Systems
In this video I go over a new chapter in my calculus book and cover Vectors and the Geometry of Space. More specifically, I cover the first section of that chapter which is on Three Dimensional Coordinate Systems. This section defines the terminology and conventions for 3D coordinates which I will be using throughout this chapter. Several examples are included such as the equations for a sphere and the distance between points in 3D.
The topics covered in this video are listed below with their time stamps.
- Introduction: 0:00
- Topics to Cover: 1:01
- Vectors and the Geometry of Space: 1:31
- Three-Dimensional Coordinate Systems: 3:02
- Example 1: 22:00
- Note on Context: 26:32
- Equations of Vertical or Horizontal Planes: 27:30
- Example 2: 32:03
- Example 3: 36:47
- Distance Formula in 2D: 39:43
- Distance Formula in Three Dimensions: 41:32
- Example 4: 52:11
- Example 5: 54:33
- Equation of a Sphere: 57:40
- Example 6: 58:45
- Example 7: 1:06:23
Watch Video On:
- 3Speak: https://3speak.tv/watch?v=mes/vdmsfims
- Odysee: https://odysee.com/@mes:8/vector-space-and-geometry-3d-coordinate:7
- BitChute: https://www.bitchute.com/video/8FSwQ9pBvz8a/
- Rumble: https://rumble.com/v1owz23-vector-space-and-geometry-3d-coordinate-systems.html
- DTube:
- YouTube: https://youtu.be/xJ-qPJFf2gE
Download Video Notes: https://1drv.ms/b/s!As32ynv0LoaIiZtLKWAWmO-eeJizjQ?e=gbHcyw
View video sections playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0GiAJeLMzhOsrMliibfce5m
View the full Vectors and Geometry of Space video series: https://www.youtube.com/playlist?list=PLai3U8-WIK0FjJpwnxwdrOR7L8Ul8VZoZ
View Video Notes Below!
Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate
Buy MES merchandise! https://mes.fm/store
More links: https://linktr.ee/matheasy
More links: https://linktr.ee/matheasyReuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Recommended Books:
- "Where Did the Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
MES Links Telegram channel: https://t.me/meslinks
Subscribe to MES Truth: https://mes.fm/truthJoin my forums!
- Hive community: https://peakd.com/c/hive-128780
- Reddit: https://reddit.com/r/AMAZINGMathStuff
- Discord: https://mes.fm/chatroom
Follow along my epic video series:
- #MESScience: https://mes.fm/science-playlist
- #MESExperiments: https://peakd.com/mesexperiments/@mes/list
- #AntiGravity: https://peakd.com/antigravity/@mes/series
-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept!- #FreeEnergy: https://mes.fm/freeenergy-playlist
- #PG (YouTube-deleted series): https://peakd.com/pg/@mes/videos
NOTE #1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website- Download and read video notes.
- Read notes on the Hive blockchain #Hive
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations:
- Increase video speed: https://mes.fm/videospeed-extension
- Increase video audio: https://mes.fm/volume-extension
- Text to speech: https://mes.fm/speech-extension
--Android app: https://mes.fm/speech-android
Calculus Book Reference
Note that I mainly follow along the following calculus book.
- Calculus: Early Transcendentals 7th Edition by James Stewart
- Note: The previous videos I used the 6th edition.
Topics to Cover
- Vectors and the Geometry of Space
- Three-Dimensional Coordinate Systems
- Example 1
- Note on Context
- Equations of Vertical or Horizontal Planes
- Example 2
- Example 3
- Distance Formula in 2D
- Distance Formula in Three Dimensions
- Example 4
- Example 5
- Equation of a Sphere
- Example 6
- Example 7
Vectors and the Geometry of Space
In this chapter we introduce vectors and coordinate systems for three-dimensional space.
This will be the setting for our study of the calculus of functions of two variables in future videos because the graph of such a function is a surface in space.
In this chapter we will see that vectors provide particularly simple descriptions of lines and planes in space.
Examples of the surfaces and solids we study in this chapter are paraboloids (used for satellite dishes) and hyperboloids (used for cooling towers of nuclear reactors).


https://grimstad.uia.no/perhh/phh/fag/matem/MA209/formel/MA209_Formel_conic.pdf
Retrieved: 1 October 2022
Archive: https://web.archive.org/save/https://grimstad.uia.no/perhh/phh/fag/matem/MA209/formel/MA209_Formel_conic.pdf
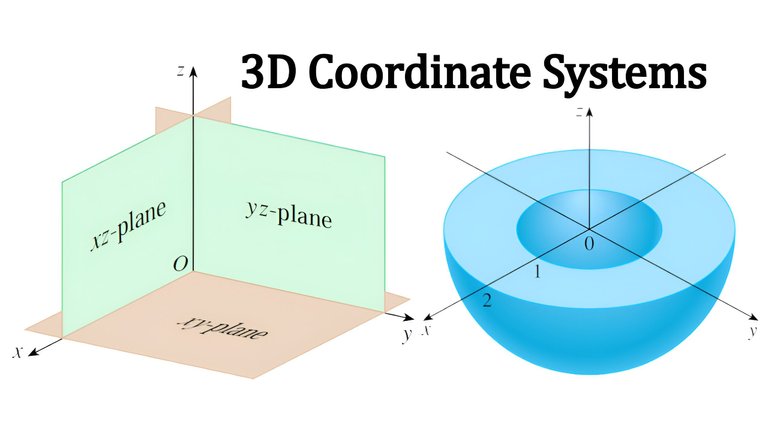
Three-Dimensional Coordinate Systems
To locate a point in a plane, two numbers are necessary.
We know that any point in the plane can be represented as an ordered pair (a, b) of real numbers, where a is the x-coordinate and b is the y-coordinate.
For this reason, a plane is called two-dimensional.
To locate a point in space, three numbers are required.
We represent any point in space by an ordered triple (a, b, c) of real numbers.
In order to represent points in space, we first choose a fixed point O (the origin) and three directed lines through O that are perpendicular to each other, called the coordinate axes and labeled the x-axis, y-axis, and z-axis.
Usually we think of the x- and y-axes as being horizontal and the z-axis being vertical, and we draw the orientation of the axis as in the figure below.
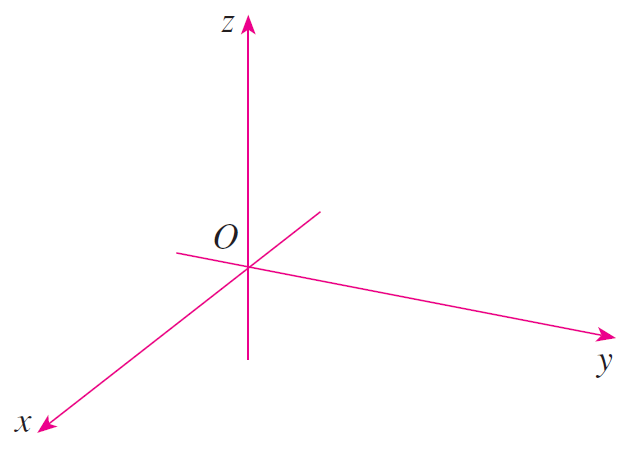
Coordinate axes
The direction of the z-axis is determined by the right-hand rule as illustrated below.
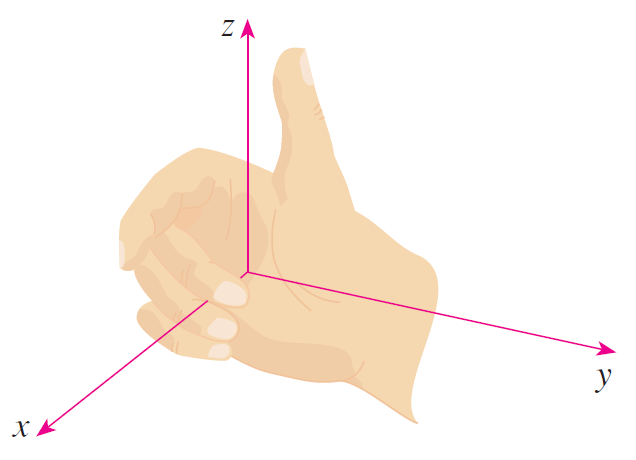
Right-hand rule
If you curl the fingers of your right hand around the z-axis in the direction of a 90° counterclockwise rotation from the positive x-axis to the positive y-axis, then your thumb points in the positive direction of the z-axis.
The three coordinate axes determine the three coordinate planes illustrated in the figure (a) below.
The xy-plane is the plane that contains the x- and y-axes; the yz-plane contains the y- and z-axes; the xz-plane contains the x- and z-axes.
These three coordinate planes divide space into eight parts, called octants.
The first octant, in the foreground, is determined from the positive axes.
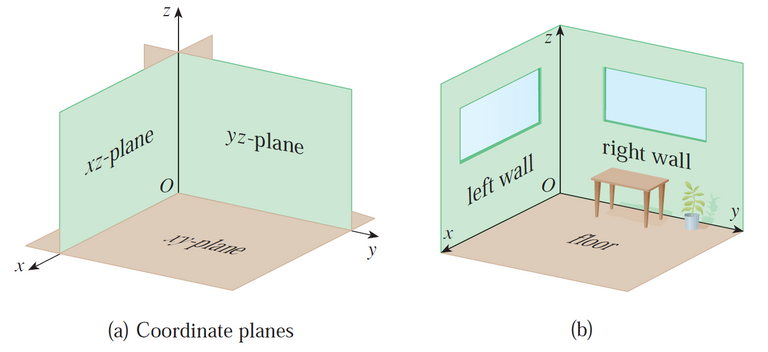
Because many people have some difficulty visualizing diagrams of three-dimensional figures, you may find it helpful to do the following (see figure (b) above).
Look at the bottom corner of a room and call the corner the origin.
The wall on your left is in the xz-plane, the wall on your right is in the yz-plane, and the floor is in the xy-plane.
The x-axis runs along the intersection of the floor and the left wall.
The y-axis runs along the intersection of the floor and the right wall.
The z-axis runs up from the floor toward the ceiling along the intersection of the two walls.
You are situated in the first octant, and you can now imagine seven other rooms situated in the other seven octants (three on the same floor and four on the floor below), all connected by the common corner point O.
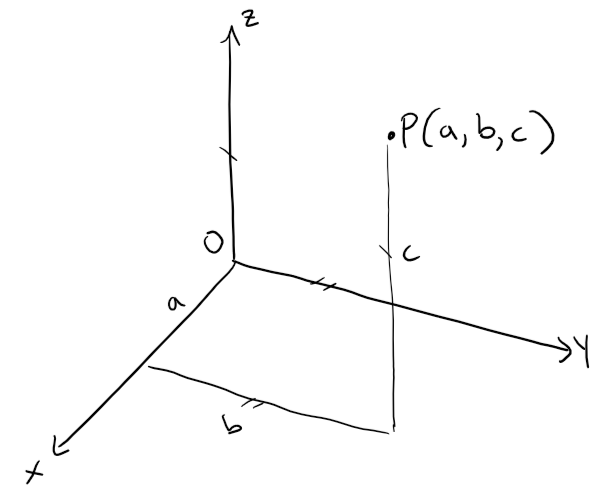
Now if P is any point in space, let a be the (directed) distance from the yz-plane to P, let b be the distance from the xz-plane to P, and let c be the distance from the xy-plane to P.
We present the point P by the ordered triple (a, b, c) of real numbers and we call a, b, and c the coordinates of P; a is the x-coordinate, b is the y-coordinate, and c is the z-coordinate.
Thus, to locate the point (a, b, c), we can start at the origin O and move a units along the x-axis, then b units parallel to the y-axis, then c units parallel to the z-axis as in the figure below.
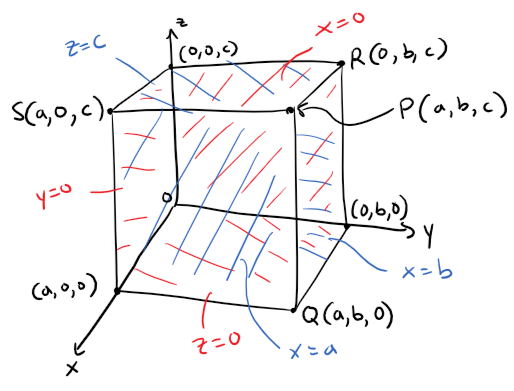
The point P(a, b, c) determines a rectangular box as in the figure below.
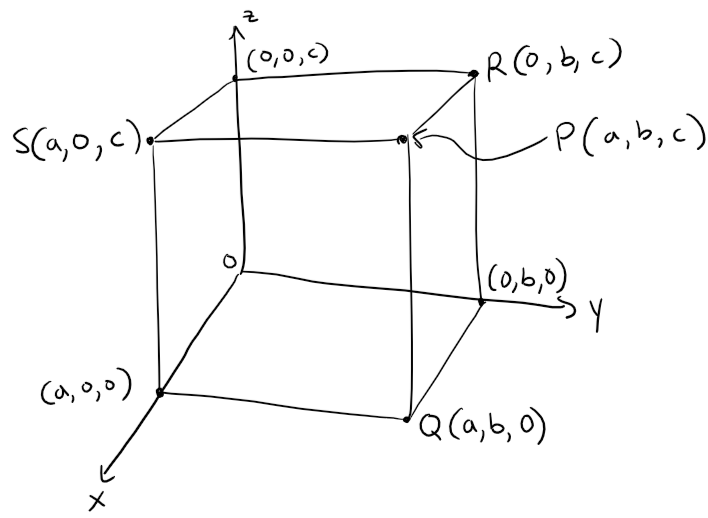
If we drop the vertical perpendicular line from P to the xy-plane, we get a point Q with coordinates (a, b, 0) called the projection of P onto the xy-plane.
Similarly, R(0, b, c) and S(a, 0, c) are the projections of P onto the yz-plane and xz-plane, respectively.
As numerical illustrations, the points (-4, 3, -5) and (3, -2, -6) are plotted in the figures below.

The following Cartesian product is the set of all ordered triples of real numbers and is denoted by ℝ3 (Latin capital R), which I sometimes just use R3 instead.
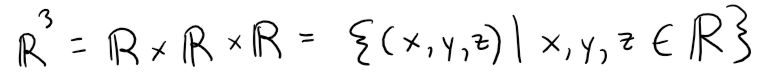
We have given a one-to-one correspondence between points P in space and ordered triples (a, b, c) in R3.
It is called a dimensional rectangular coordinate system.
Notice that, in terms of coordinates, the first octant can be described as the set of points whose coordinates are all positive.
In two-dimensional analytic geometry, the graph of an equation involving x and y is a curve in R2.
In three-dimensional analytic geometry, an equation in x, y, and z represents a surface in R3.
Example 1
What surfaces in R3 are represented by the following equations?
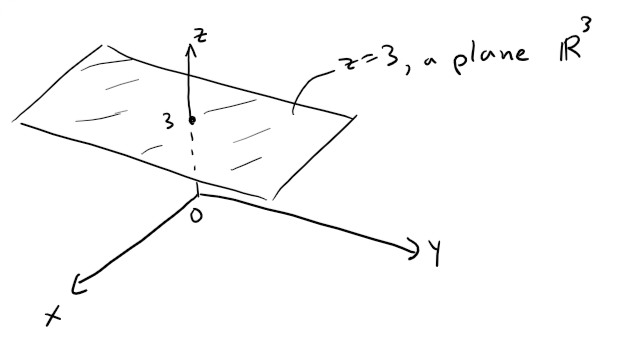
(a) z = 3
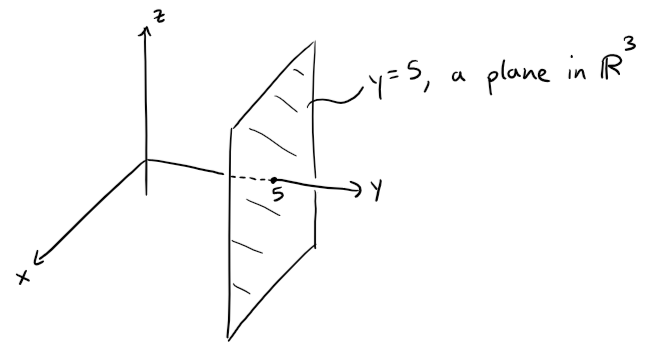
(b) y = 5
Solution to (a):
The equation z = 3 represents the set {(x, y, z) | z = 3}, which is the set of all points in R3 whose z-coordinate is 3.
This is the horizontal plane that is parallel to the xy-plane and three units above it as in the figure below.
Solution to (b):
The equation y = 5 represents the set of all points in R3 whose y-coordinate is 5.
This is the vertical plane that is parallel to the xz-plane and five units to the right of it as in the figure below.
Note on Context
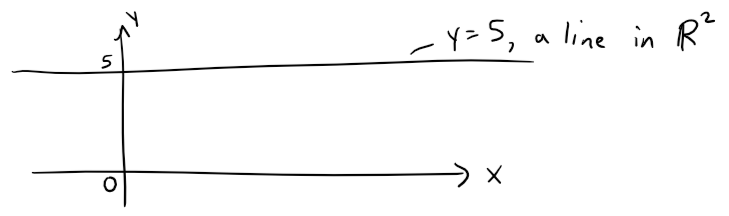
When an equation is given, we must understand from the context where it represents a curve in R2 or a surface in R3.
In Example 1, y = 5 represents a plane in R3, but of course y = 5 can also represent a line in R2 if we are dealing with two-dimensional analytic geometry, as in the figure below.
Equations of Vertical or Horizontal Planes
In general, if k is a constant, then:
x = k represents a vertical plane parallel to the yz-plane,
y = k is a vertical plane parallel to the xz-plane,
z = k is a horizontal plane parallel to the xy-plane.
In the earlier rectangular box figure above (copied below too), the faces of the rectangular box are formed by the three coordinate planes:
x = 0 (the yz-plane)
y = 0 (the xz-plane)
z = 0 (the xy-plane)and
x = a
y = b
z = c
Example 2
(a) Which points (x, y, z) satisfy the equations:
x2 + y2 = 1 and z = 3.
(b) What does the equation x2 + y2 = 1 represent as a surface in R3?
Solution to (a):
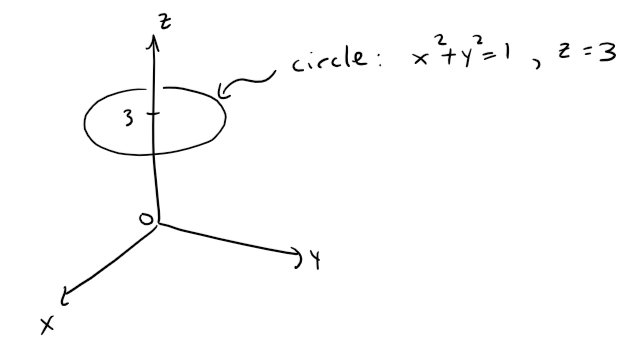
Because z = 3, the points lie in the horizontal plane z = 3, from Example 1(a).
Because x2 + y2 = 1, the points lie on the circle with radius 1 and center on the z-axis, as shown in the figure below.
Solution to (b):
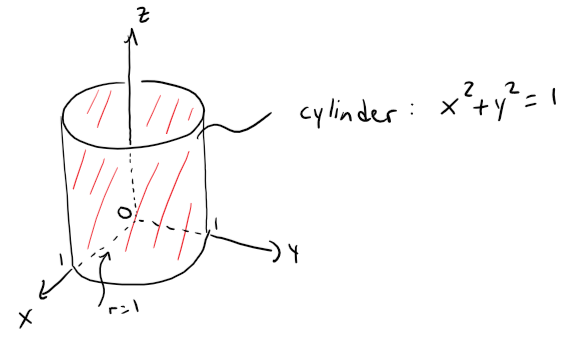
Given that x2 + y2 = 1, with no restrictions on z, we see that the point (x, y, z) could lie on a circle in any horizontal plane z = k.
So the surface x2 + y2 = 1 in R3 consists of all possible horizontal circles x2 + y2 = 1, z = k, and is therefore the circular cylinder with radius 1 whose axis is the z-axis.
Example 3
Describe and sketch the surface in R3 represented by the equation y = x.
Solution:
The equation represents the set of all points in R3 whose x- and y-coordinates are equal, that is:
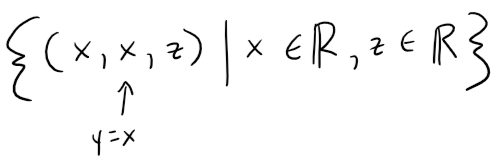
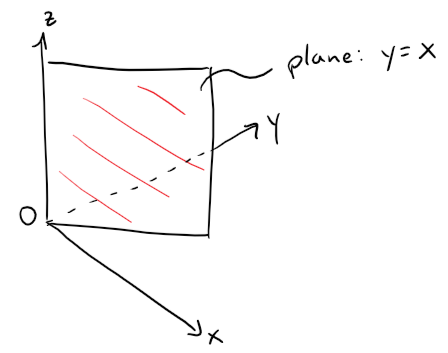
This is a vertical plane that intersects the xy-plane in the line y = x, z = 0.
The portion of this plane that lies in the first octant is sketched in the figure below.
Distance Formula in 2D
Recall the 2D distance formula between 2 points.
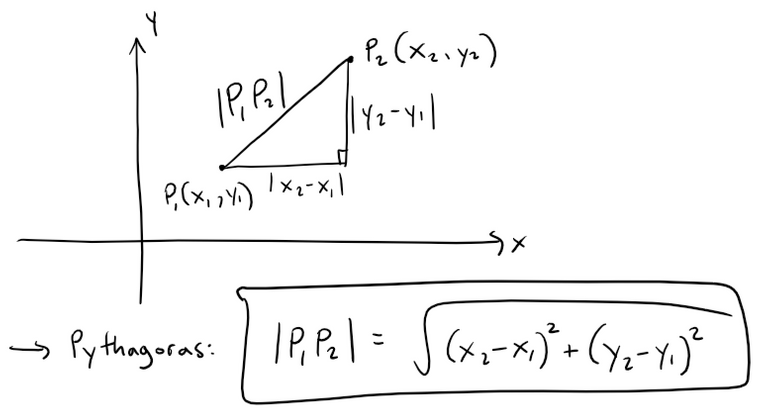
The familiar formula for the distance between two points in a plane is easily extended to the following three-dimensional formula:
Distance Formula in Three Dimensions
The distance |P1P2| between the points P1(x1, y1, z1) and P2(x2, y2, z2) is:
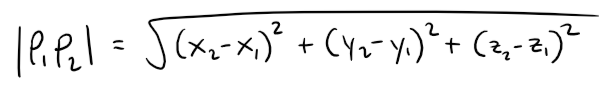
Proof:
To see why this formula is true, we construct a rectangular box as in the figure below, where P1 and P2 are opposite vertices and the faces of the box are parallel to the coordinate planes.
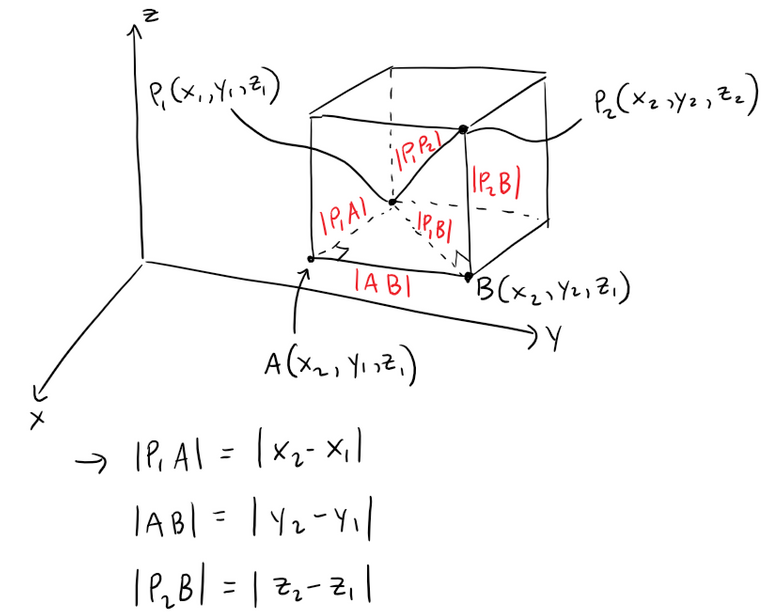
Because triangles P1BP2 and P1AB are both right-angled, two applications of the Pythagorean Theorem give:
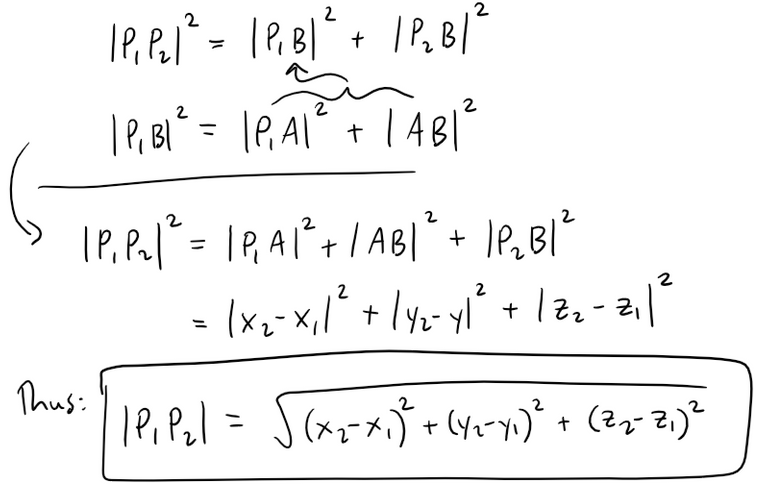
Example 4
The distance from the point P(2, -1, 7) to the point Q(1, -3, 5) is:

Example 5
Find an equation of a sphere with radius r and center C(h, k, L).
Solution:
By definition, a sphere is the set of all points P(x, y, z) whose distance from C is r, see figure below.
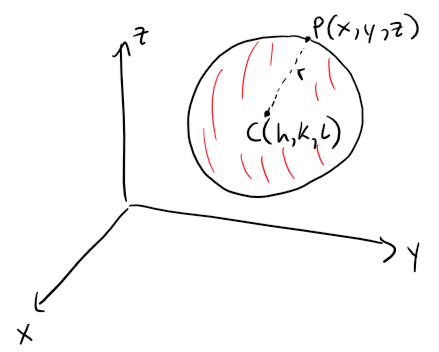
Thus P is on the sphere if and only if the distance |PC| = r.
Squaring both sides, we have:
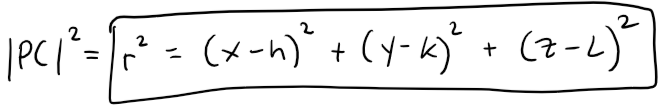
The result of Example 5 is worth remembering.
Equation of a Sphere
An equation of a sphere with center C(h, k, L) and radius r is:
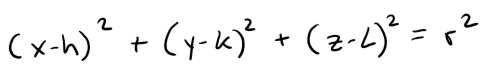
In particular, if the center is the origin O, then an equation of the sphere is:
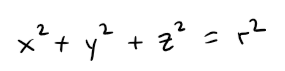
Example 6
Show that the following is the equation of a sphere, and find its center and radius.
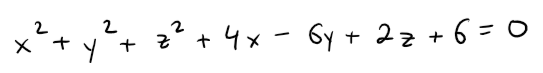
Solution:
We can rewrite the given equation in the form of an equation of a sphere if we complete squares:
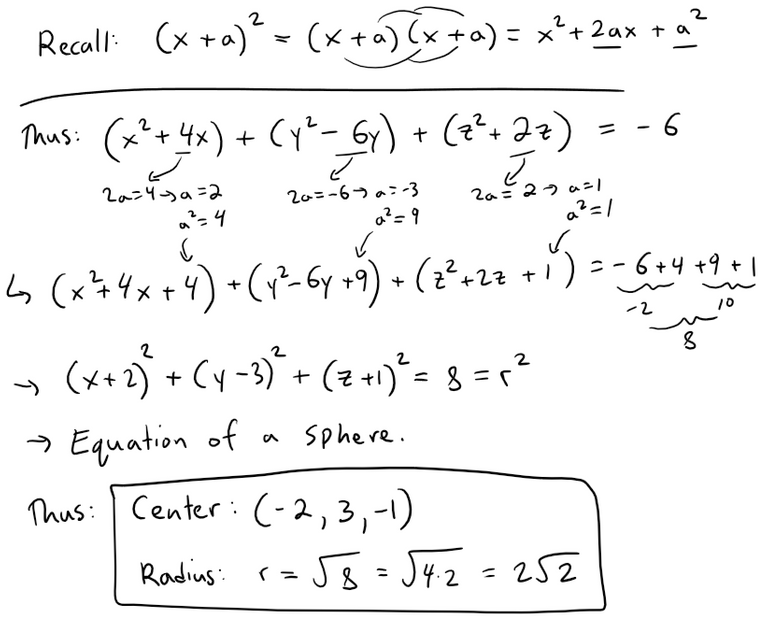
Here's a graph of the sphere using the GeoGebra 3D graphing calculator:
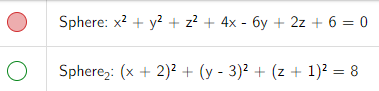

Example 7
What region in R3 is represented by the following inequalities?
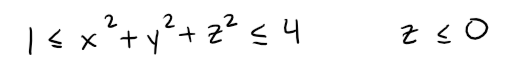
Solution:
The inequalities can be rewritten as:
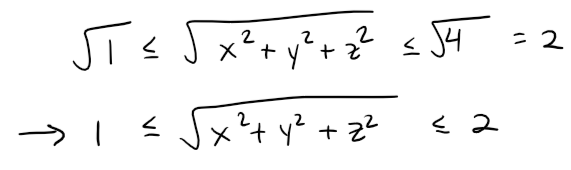
These represent the points (x, y, z) whose distance from the origin is at least 1 and at most 2.
But we are also given that z ≤ 0, so the points lie on or below the xy-plane.
Thus the given inequalities represent the solid region that lies beneath (or on) the xy-plane and between (or on) the spheres:

Let's double check our work using the GeoGebra 3D graphing calculator:

