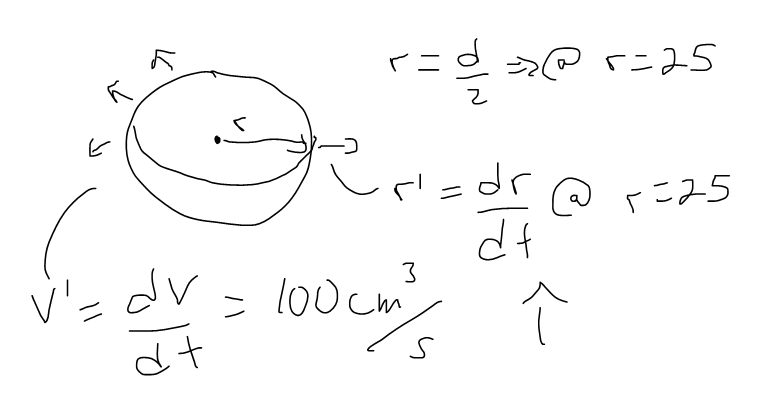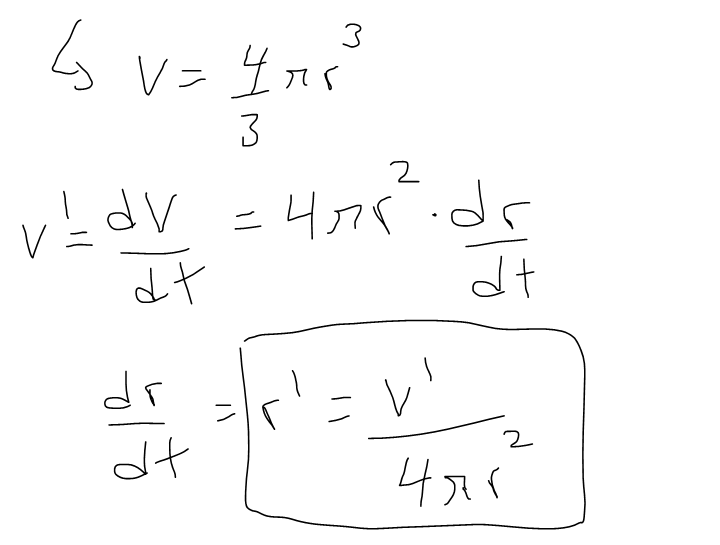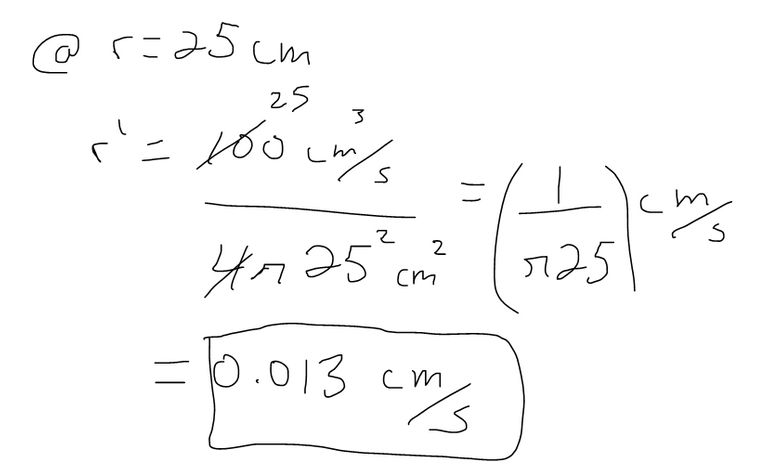Related Rates: Introduction + Balloon Problem
In this video I go over a brief introduction on related rates and then solve an example inflating a spherical balloon to help further illustrate the basic concepts of related rates.
Watch video on:
- BitChute: https://www.bitchute.com/video/6qJYpZ39vvIK/
- DTube: https://d.tube/#!/v/mes/QmbsMSRNSgmEJPiisSNyYF6wPAg1to9EfFUPnLVygUKSv4
- YouTube: https://youtu.be/oYU51dBqWo0
Download video notes: https://1drv.ms/b/s!As32ynv0LoaIg4ZnNkruAlXggAHVIA?e=Ao6OZT
View Video Notes Below!
Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donateReuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Join my private Discord chat room: https://mes.fm/chatroom
Check out my Reddit and Voat math forums:
Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Follow along my epic video series:
- #MESScience: https://mes.fm/science-playlist
- #MESExperiments: https://peakd.com/mesexperiments/@mes/list
- #AntiGravity: https://peakd.com/antigravity/@mes/series
-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept!- #FreeEnergy: https://mes.fm/freeenergy-playlist
NOTE #1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed. (#Try2xSpeed)
-- Try 4X+ speed by browser extensions or modifying source code.
-- Browser extension recommendation: https://mes.fm/videospeed-extension
-- See my tutorial to learn more: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website- Download and read video notes.
- Read notes on the Hive blockchain #Hive
- Watch the video in parts.
NOTE #2: If video volume is too low at any part of the video:
- Download this browser extension recommendation: https://mes.fm/volume-extension
Related Rates: Intro + Balloon Example

Introduction
- If we are pumping air into a balloon both the volume and the radius are increasing and their rates of increase are related to each other.
- But it is much easier to measure directly the rate of increase of the volume than the rate of increase of the radius.
- This is because we can easily pump a known volume of air, for example, without worrying about the geometry (which we would need if measuring the radius)
- In a related rates problem the idea is to compute the rate of change of one quantity in terms of the rate of change of another quantity (which may be more easily measured).
- The procedure is to find an equation that relates the two quantities and then use the Chain Rule to differentiate both sides with respect to time.
Example
Air is being pumped into a spherical balloon so that its volume increases at a rate of 100 cm3/s. How fast is the radius of the balloon increasing when the diameter is 50 cm?
Solution