Leibniz’s Rule: Generalization of the Product Rule for Derivatives

avatar
(Edited)

In this video I go over Leibniz’s rule which is the generalization of the product rule for derivatives and extends it for all derivatives and not just the first one. I had covered the product rule in my earlier video and showed that the derivative of the product (f·g)’ = f’g + fg’. We can use this same product rule, along with mathematical induction, to prove the general Leibniz rule for the n-th derivative of the product (f·g) (n).

Leibniz’s rule makes use of the binomial coefficient which I had briefly discussed in a prior video as well. After I prove the rule, I manually derive consecutive derivatives using the product rule, as well as comparing the result with the binomial theorem. I do this to show the amazing synchronicity or similarity between the powers of a binomial (x + y)n and the derivative of a product (f·g) (n).

The topics covered in this video are listed below with their time stamps.

  • @ 0:42 - Topics to Cover
  1. @ 1:14 - Recap on the Product Rule for Derivatives
  2. @ 2:51 - Leibniz's Rule: Generalization of the Product Rule for Derivatives
    • @ 8:00 - Proof of Leibniz's Rule
    • @ 45:17 - Manually Determining the n-th Derivative Using the Product Rule
    • @ 59:27 - Synchronicity with the Binomial Theorem

Watch video on:

Download Video Notes: https://1drv.ms/b/s!As32ynv0LoaIiLYb3IimifHz3HfzeQ?e=rch7UF

View Video Notes Below!

Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate

Reuse of my videos:

  • Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.

Fight back against censorship:

  • Bookmark sites/channels/accounts and check periodically
  • Remember to always archive website pages in case they get deleted/changed.

Join my private Discord chat room: https://mes.fm/chatroom

Check out my Reddit and Voat math forums:

Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Follow along my epic video series:

NOTE #1: If you don't have time to watch this whole video:

NOTE #2: If video volume is too low at any part of the video:

Leibniz's Rule: Generalization of the Product Rule for Derivatives

General Leibniz Product Rule.jpeg

Topics to Cover

  1. Recap on the Product Rule for Derivatives
  2. Leibniz's Rule: Generalization of the Product Rule for Derivatives
    • Proof of Leibniz's Rule
    • Manually Determining the n-th Derivative Using the Product Rule
    • Synchronicity with the Binomial Theorem

Recap on the Product Rule for Derivatives

Recall from my earlier video in which I covered the product rule for derivatives.

https://youtu.be/EIjvGJhDAOk

Retrieved: 7 August 2020
Video notes archive: https://archive.vn/tbpU2

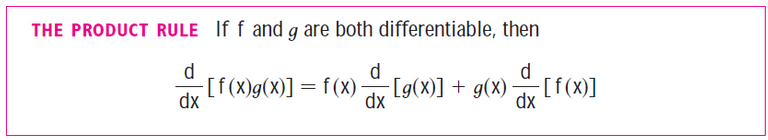
image.png

Note that we can also write the product rule in the following equivalent notation:

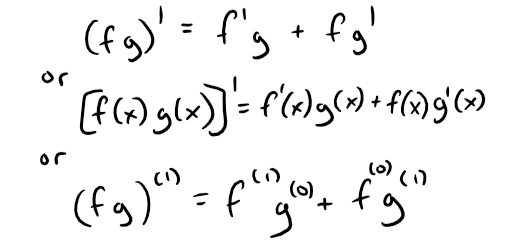
image.png

Leibniz's Rule: Generalization of the Product Rule for Derivatives

The following generalization of the product rule is known as the Leibniz's rule or general Leibniz rule, named after Gottfried Wilhelm Leibniz, and the proof is taken from Wikipedia:

https://en.wikipedia.org/wiki/General_Leibniz_rule

Retrieved: 8 August 2020
Archive: https://archive.vn/wip/c2TDz

General Leibniz Rule

In calculus, the general Leibniz rule,[1] named after Gottfried Wilhelm Leibniz, generalizes the product rule (which is also known as "Leibniz's rule"). It states that if f and g are n-times differentiable functions, then the product f·g is also n-times differentiable and its n-th derivative is given by

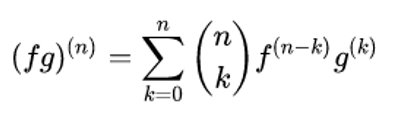
image.png

where

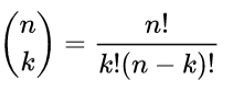
image.png

is the binomial coefficient and f(j) denotes the j-th derivative of f (and in particular f(0) = f).

The rule can be proved by using the product rule and mathematical induction.

Note again the different equivalent derivative notations.

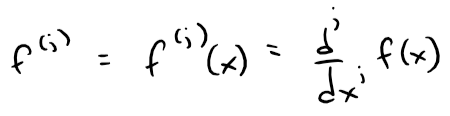
image.png

Thus we can write Leibniz's rule in the more formal derivative notation as well as in an equivalent alternative form.

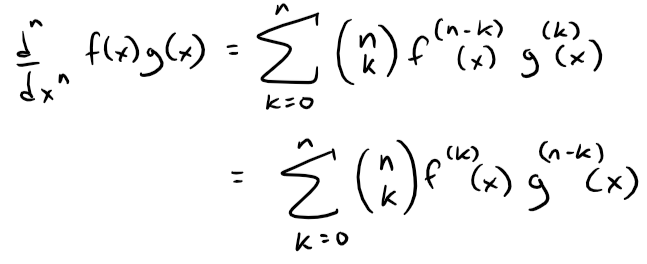
image.png

Proof of Leibniz's Rule

The proof involves the principle of mathematical induction, referenced from my earlier video.

https://youtu.be/WdIr_onvUtE

Retrieved: 2 July 2019
Archive: http://archive.fo/4lslc

image.png

When n = 1, the Leibniz Rule becomes just the product rule for derivatives.

image.png

Note that 0! is defined as equal to 1.

Thus we know that the Leibniz' rule is true for n = 1, i.e. the product rule.

Let's assume it is true for a fixed n-th derivative where n ≥ 1:

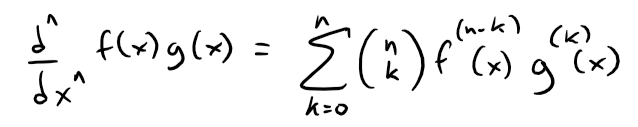
image.png

The next step in mathematical induction is to prove it is true for n + 1 which we will do so using the product rule.

Thus, taking the derivative we have:

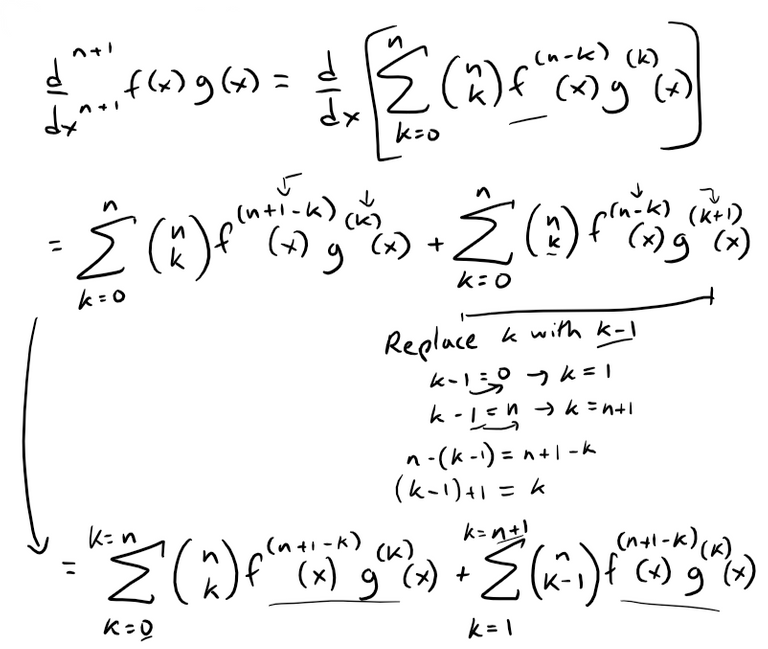
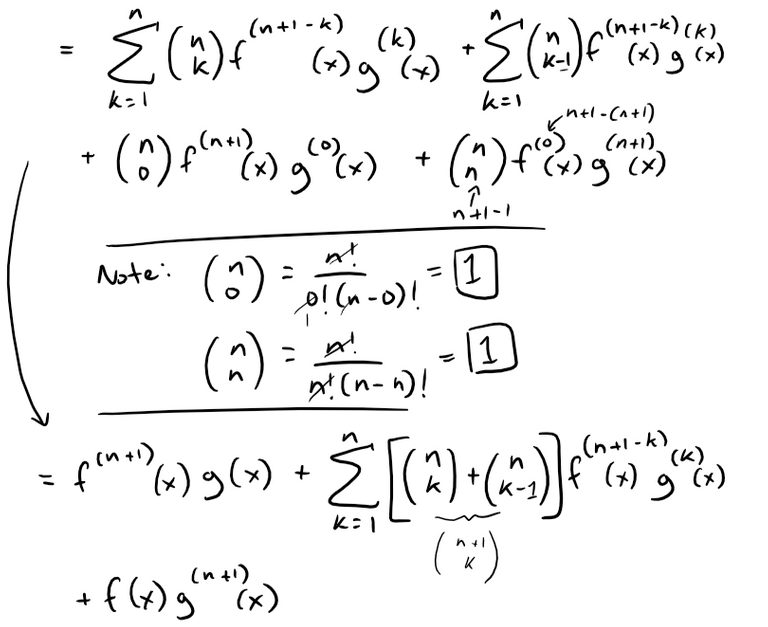
image.png

image.png

Note we can simplify the binomial coefficients by expanding and adding together.

image.png

Thus, we can continue simplifying our derivative.

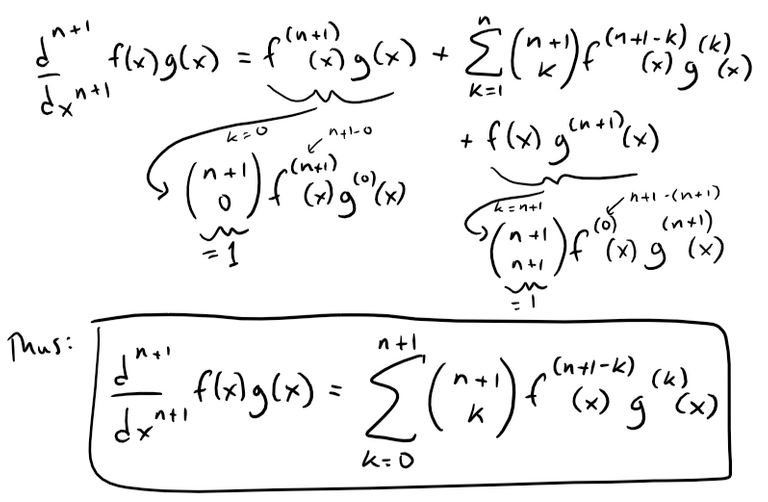
image.png

This is the result if we had just used Leibniz's rule and replaced n with n + 1.

Thus, our mathematical induction is complete and Leibniz's rule is true for all derivatives or for all n ≥ 1.

Manually Determining the n-th Derivative Using the Product Rule

We can see the pattern that arises when we manually derive the consecutive derivatives of the product of functions f and g.

Note that I will be using the short form derivative notation:

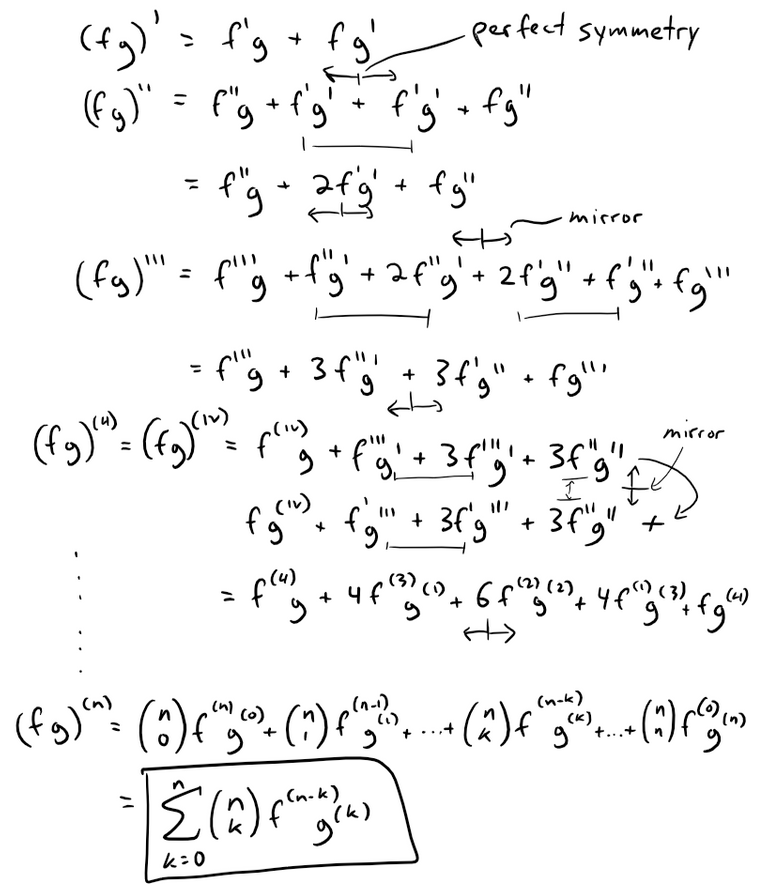
image.png

The pattern extends as expected based on Leibniz's rule.

Synchronicity with the Binomial Theorem

The Leibniz's rule is almost identical in appearance with the binomial theorem.

The binomial theorem involves the n-th power of a binomial (which is sum of two monomials or single termed polynomials) while Leibniz's rule involves the n-th derivative of a product of two functions.

And the binomial coefficients (or Leibniz's rule coefficients) can be determined easily by using Pascal's triangle as explained in my earlier video.

https://peakd.com/@mes/infinite-sequences-and-series-representations-of-functions-as-power-series
Retrieved: 6 August 2020
Archive: https://archive.vn/wip/JsH4l

https://en.wikipedia.org/wiki/Binomial_theorem

Retrieved: 26 December 2019
Archive: https://archive.ph/7hDUV

Binomial theorem

In elementary algebra, the **binomial theorem **(or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial (x + y)n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b + c = n, and the coefficient a of each term is a specific positive integer depending on n and b. For example (for n = 4),

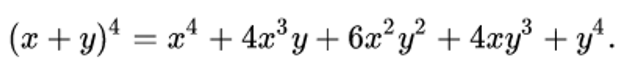
image.png

The coefficient a in the term of axbyc is known as the binomial coefficient:

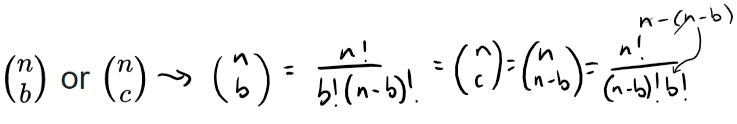
image.png

(the two have the same value). These coefficients for varying n and b can be arranged to form Pascal's triangle. These numbers also arise in combinatorics, where (nb) gives the number of different combinations of b elements that can be chosen from an n-element set. Therefore (nb) is often pronounced as "n choose b".

image.png

The binomial coefficient (nb) appears as the bth entry in the nth row of Pascal's triangle (counting starts at 0). Each entry is the sum of the two above it.

…

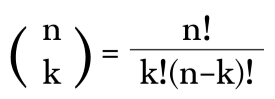
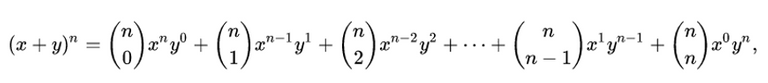
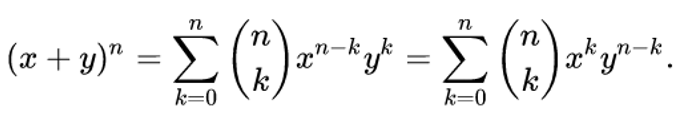
image.png

…

image.png

…

image.png

MES Note: Note the symmetry in the formula and terms.

As a comparison we have:

image.png

mathematics calculus science messcience math stem education hiveeducation leibniz tutorial
0
0
0.000
0 comments