Laboratory Project: An Elusive Limit

avatar
(Edited)

In this video I go over the Laboratory Project titled An Elusive Limit. Laboratory Projects are interesting math projects at the end of some sections of my calculus book, and in this case at the end of the section on Taylor and Maclaurin Series. The project I cover involves solving the limit of a function that has a difference in the numerator and denominator; and both include trigonometric sine and tangent functions, as we well as inverse trigonometric sine and tangent functions.

The interesting part of all of these functions is that as x approaches 0, then they all approach 0 in about the same rate so that their values are near identical to a high level of digits precision. This makes the resulting differences in the numerator and denominator of the function cancel out most of the digits and thus we are left with only a few correct decimal places. This makes the resulting calculations highly dependent on the level of precision of the calculator being used, and in most cases the calculator won’t be able to brute force calculate the function at values very close to x = 0.

In this case we can still solve the limit in several ways, either by using a computer algebra system (CAS) to solve derivatives or power series of the numerator and denominator, and thus be able to use methods such as l’Hospital’s Rule or other limit laws and algebra manipulation. This effectively means that if we can’t compute the function directly we can instead focus on simplifying or transforming the numerator and denominator into their equivalent but different formulations, which may allow for the limit to be solved through algebraic or calculus means.

This is a very interesting tutorial involving the use of calculators and understanding the levels of precision to be certain that the calculations are correct, so make sure to watch this video!

The topics covered in this video are listed below with their time stamps.

  • @ 1:12 - Topics to Cover
  1. @ 1:33 - Laboratory Project: An Elusive Limit
    • 6 Questions
  2. Solutions
    • @ 3:13 - Solution to Question 1
    • @ 19:51 - Solution to Question 2
    • @ 21:14 - Solution to Question 3
    • @ 28:40 - Solution to Question 4
    • @ 41:12 - Solution to Question 5
    • @ 43:13 - Solution to Question 6

Watch Video On:

Download Video Notes: https://1drv.ms/b/s!As32ynv0LoaIiL8FaIRCuICnLYyMZg?e=o1tMub

View Video Notes Below!

Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate
Buy MES merchandise! https://mes.fm/store
More links: https://linktr.ee/matheasy

Reuse of my videos:

  • Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.

Fight back against censorship:

  • Bookmark sites/channels/accounts and check periodically
  • Remember to always archive website pages in case they get deleted/changed.

Recommended Books:

Subscribe to MES Truth: https://mes.fm/truth
MES Links Telegram channel: https://t.me/meslinks

Join my forums!

Follow along my epic video series:

NOTE #1: If you don't have time to watch this whole video:

Browser extension recommendations:

Laboratory Project: An Elusive Limit

Laboratory Project An Elusive Limit.jpeg

Calculus Book Reference

Note that I mainly follow along the following calculus book:

Calculus: Early Transcendentals Sixth Edition by James Stewart

Note that "Laboratory Projects" are interesting math projects at the end of several sections in my calculus book, and in this case it is at the end of the section on Taylor and Maclaurin Series.

Topics to Cover

  1. Laboratory Project: An Elusive Limit
    • 6 Questions
  2. Solutions
    • Solution to Question 1
    • Solution to Question 2
    • Solution to Question 3
    • Solution to Question 4
    • Solution to Question 5
    • Solution to Question 6

Laboratory Project: An Elusive Limit

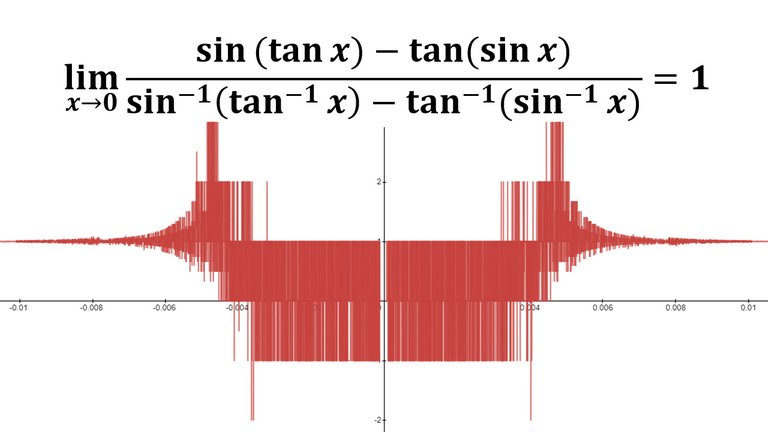
This project deals with the function:

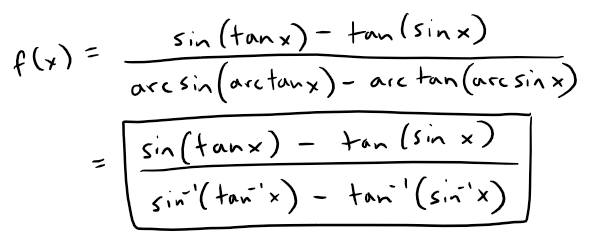
image.png

Question 1

Use your computer algebra system (CAS) to evaluate f(x) for x = 1, 0.1, 0.01, 0.001, and 0.0001.

Does it appear that f has a limit as x → 0?

Question 2

Use the CAS to graph f near x = 0.

Does it appear that f has a limit as x → 0?

Question 3

Try to evaluate limx→0 f(x) with l'Hospital's Rule, using the CAS to find derivatives of the numerator and denominator.

What do you discover?

How many applications of l'Hospital's Rule are required?

Question 4

Evaluate limx→0 f(x) by using the CAS to find sufficiently many terms in the Taylor series of the numerator and denominator.

Use the command "taylor" in Maple or "Series" in mathematica.

Question 5

Use the limit command on your CAS to find limx→0 f(x) directly.

Most computer algebra systems use the method of Question 4 to computer to compute limits.

Question 6

In view of the answers to Questions 4 and 5, how do you explain the results in Questions 1 and 2?

Solution to Question 1

The Calculus book solutions manual states it used the Maple mathematics or CAS software program, which has 10 digits of precision, to calculate the following table of values for f(x).

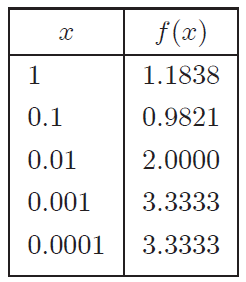
image.png

The results of this project will vary depending on the CAS and precision level.

In this case, it appears that as x → 0+, then f(x) → 10/3.

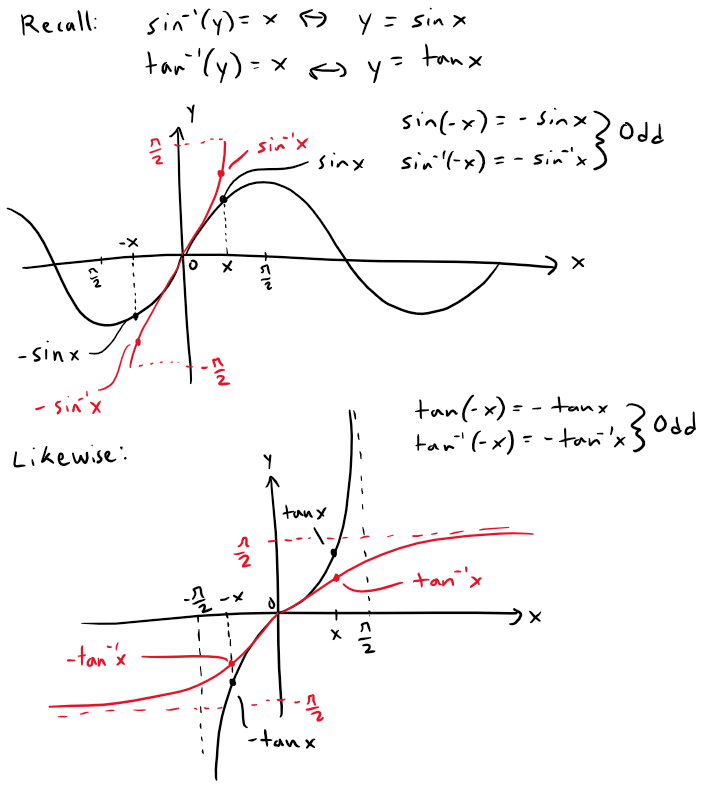
Note that f is an even function, thus f(x) → 10/3 as x → 0- and thus as x → 0.

We can show that f is an even function, that is f(-x) = f(x), as follows:

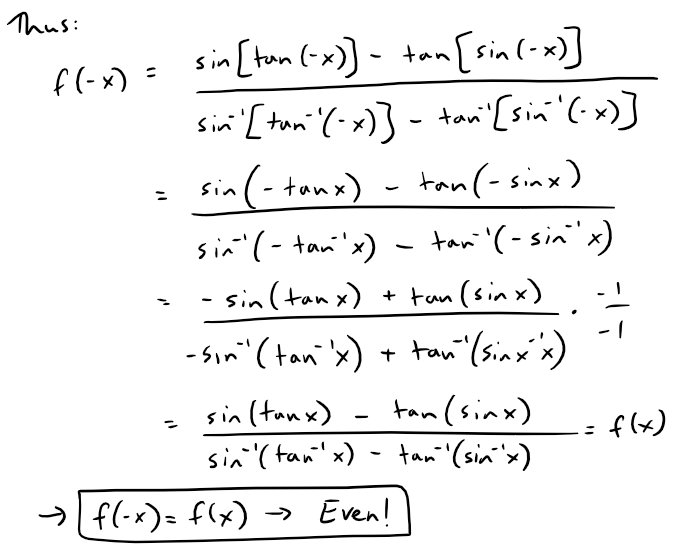
image.png

image.png

When I did the same calculations using Microsoft Excel, I get the following table of values.

https://1drv.ms/x/s!As32ynv0LoaIiL5bYefBaVp2LGff5Q?e=cJkUr1
Retrieved: 15 October 2020
Archive: Not available

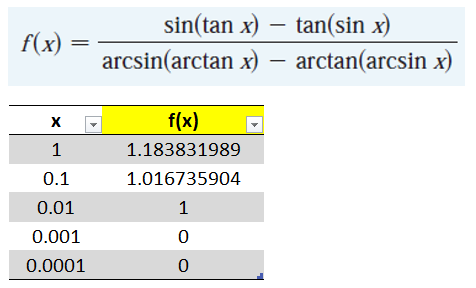
image.png

Note that Excel uses 15 digits of precision.

Using the Desmos calculator, we get the following.

https://www.desmos.com/calculator/vhwpqsail1
Retrieved: 17 October 2020
Archive: https://archive.vn/wip/IIUpm

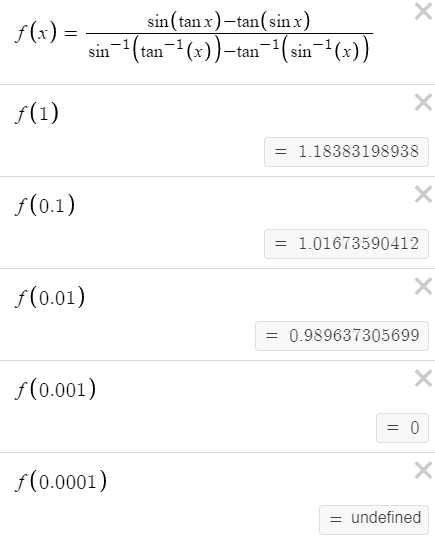
image.png

Note that Desmos uses a dynamic system between 15 and *178 digits of precision.

We can summarize below the different calculation methods:

Maple, 10 digits of precision: f(x) → 10/3 as x → 0.

Excel, 15 digits of precision: f(x) → 0 as x → 0.

Desmos, 15 to 17 digits of precision: f(x) → undefined as x → 0.

Thus, it is not clear if f has a limit or not as x → 0.

Solution to Question 2

The graph of f near x = 0, from the solutions manual, is shown below.

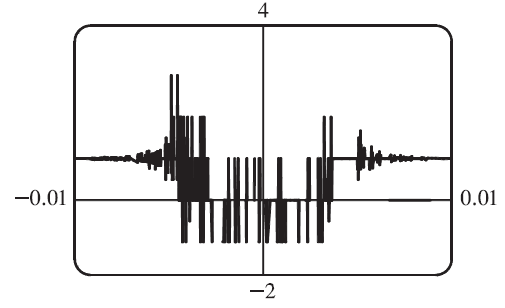
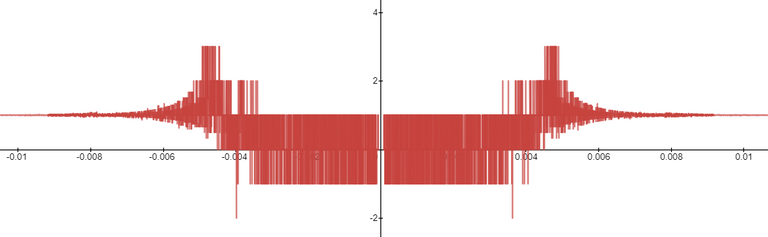
image.png

The graph is inconclusive about the limit of f as x → 0.

Likewise, the graph of f using the Desmos calculator is also unclear.

https://www.desmos.com/calculator/vhwpqsail1

image.png

Solution to Question 3

If we take the limit as x → 0 we get the indeterminate form 0/0.

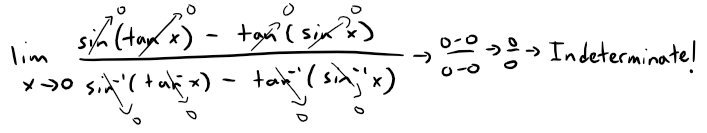
image.png

Thus we can apply l'Hospital's rule, referenced from my earlier video.

https://youtu.be/FhFWfVUBXC4
Retrieved: 3 October 2020
Video notes archive: https://archive.vn/qiZ5r

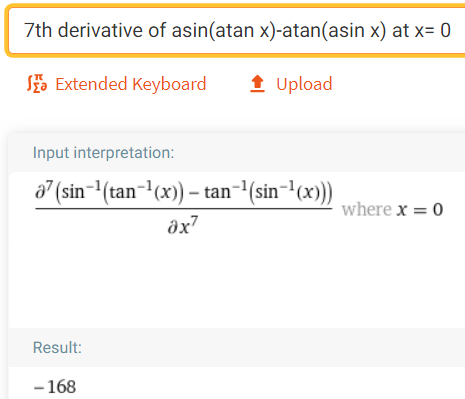
image.png

Since the Laboratory Project asks us to use a CAS to solved the derivatives of the numerator and denominator, we can use the amazing Wolfram Alpha website.

The first 6 derivatives all yield a limit of the indeterminate form 0/0.

Finally, on the seventh application of l'Hospital's Rule we obtain non-zero values!

https://www.wolframalpha.com/input/?i=7th+derivative+of+sin%28tan+x%29-tan%28sin+x%29+at+x%3D+0
Retrieved: 17 October 2020
Archive: https://archive.vn/wip/fSor5

image.png

https://www.wolframalpha.com/input/?i=7th+derivative+of+asin%28atan+x%29-atan%28asin+x%29+at+x%3D+0
Retrieved: 17 October 2020
Archive: https://archive.vn/wip/QGgUI

image.png

Thus the limit is:

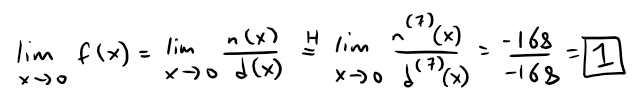
image.png

Note that n(x) and d(x) are the numerator and denominator, respectively, of f(x).

Solution to Question 4

We are now asked to solve the limit using a CAS to determine the Taylor series of the numerator and denominator.

Using our trusty Wolfram Alpha calculator, we can determine the Taylor series centered at x = 0, i.e. the Maclaurin series, for both the numerator and denominator.

https://www.wolframalpha.com/input/?i=Taylor+series+of+sin%28tan+x%29+-+tan%28sin+x%29
Retrieved: 17 October 2020
Archive: https://archive.vn/wip/E5VUH

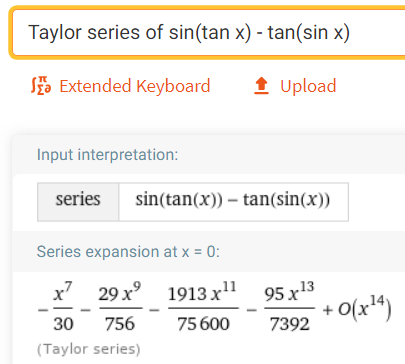
image.png

https://www.wolframalpha.com/input/?i=Taylor+series+of+asin%28atan+x%29+-+atan%28asin+x%29
Retrieved: 17 October 2020
Archive: https://archive.vn/wip/5atb2

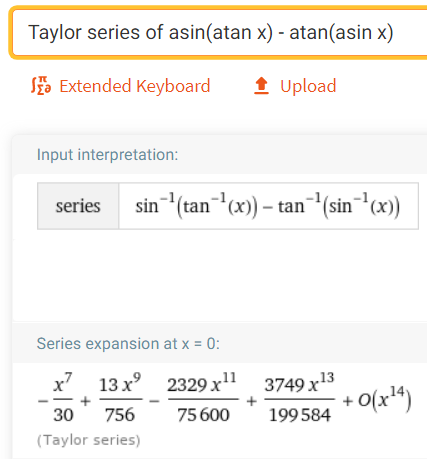
image.png

Note that the O is termed the "Big O Notation" and used to indicate that the series has a maximum absolute value beyond the evaluated terms.

In our case O(x14) indicates the series sum of the remaining terms has a maximum value at of a constant multiplied by |x14| when x is close to 0.

Learn more on here: https://en.wikipedia.org/wiki/Big_O_notation

Thus, evaluating the limit of the Taylor series, we have:

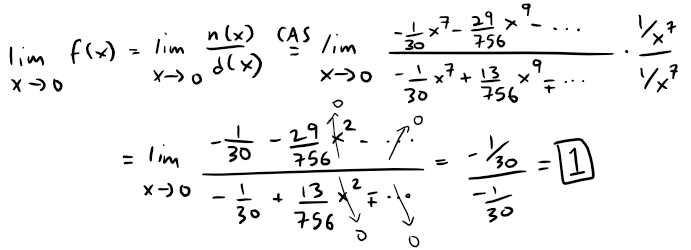
image.png

Note that we could've also applied l'Hospital's Rule to the Taylor series 7 times to obtain the same result as Question 3.

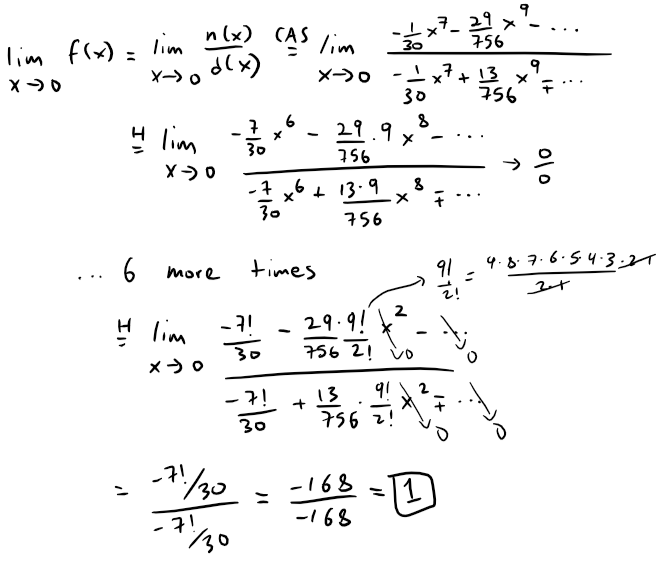
image.png

Calculation check:

7! = 5,040
-7!/30 = -168

This result agrees with the result in Question 3.

Solution to Question 5

If we calculate the limit directly using Wolfram Alpha we get the correct answer.

https://www.wolframalpha.com/input/?i=limit+of+%28sin%28tan%28x%29%29+-+tan%28sin+x%29%29%2F%28asin%28atan+x%29+-+atan%28asin+x%29%29+as+x+approaches+0
Retrieved: 17 October 2020
Archive: https://archive.vn/18SGs

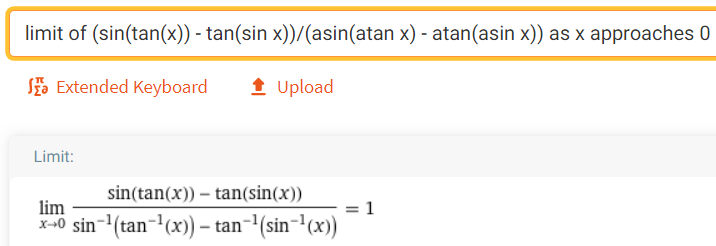
image.png

Solution to Question 6

The strange results (with only 10 to 17 digits of precision) from Question 1 and 2 must be due to the fact that the terms being subtracted in the numerator and denominator are very close in value when |x| is small.

Thus, the differences are imprecise (have few correct digits).

We can see this is the case by comparing the graphs of the terms in the numerator as well as comparing the terms in the denominator.

When we zoom in near x = 0 we see that the values of the terms are almost identical and to any level of zoom we get to.

https://www.desmos.com/calculator/vhwpqsail1

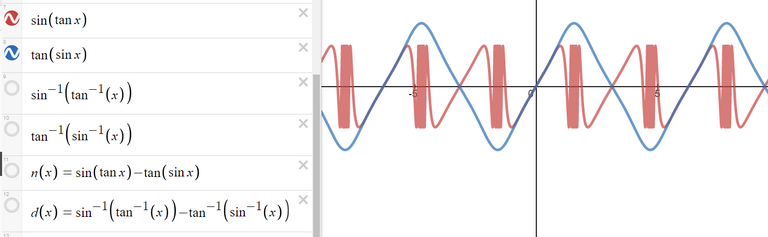
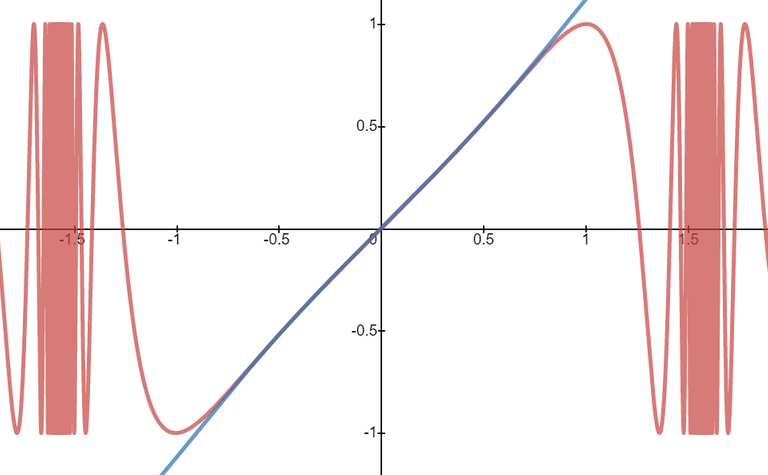
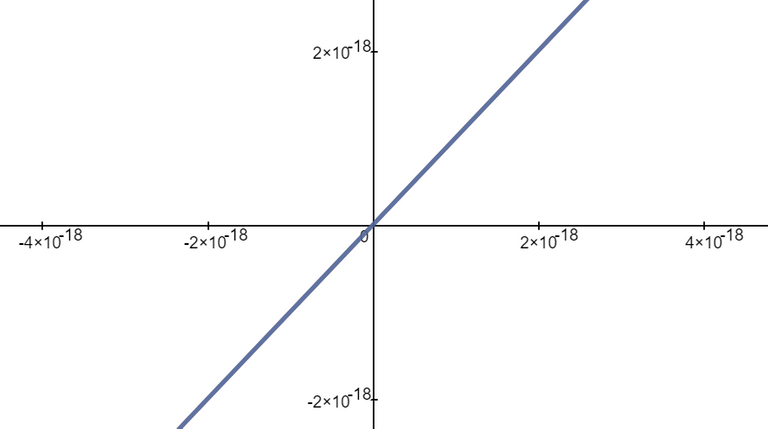
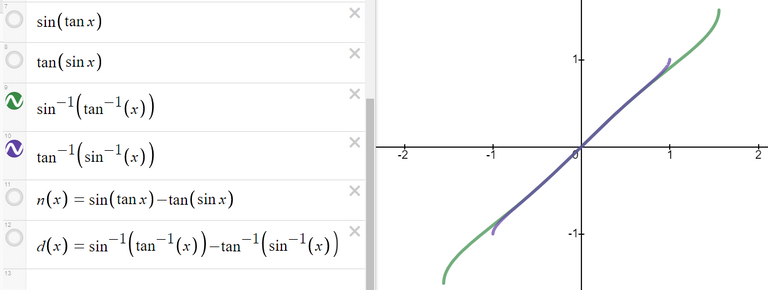
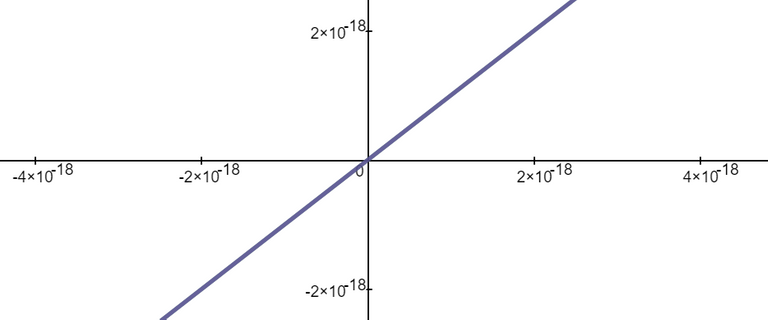
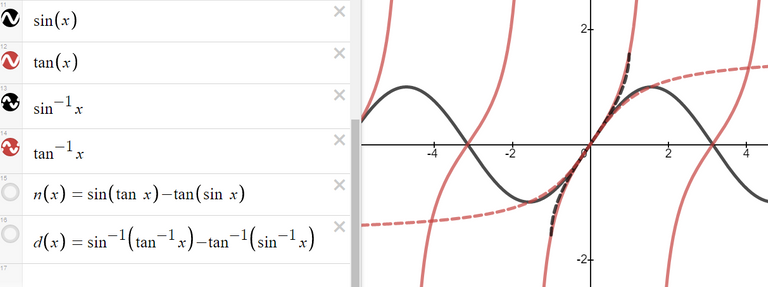
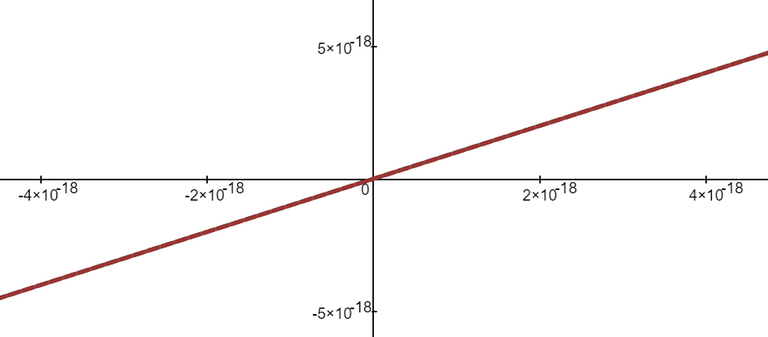
image.png

image.png

image.png

image.png

image.png

image.png

image.png

Thus, the terms themselves are near identical when zooming in beyond even the level of precision of most calculators.

To illustrate what this means, consider the following calculations of 10 digits of precision:

Division:

Exact:

0.000012345279
÷ 0.000012345111
= 1.000013608626

Calculator:

0.000012345
÷ 0.000012345
= 1.000000000

Difference:

Exact:

0.000012345279
- 0.000012345111
= 0.000000000168

Calculator:

0.000012345
- 0.000012345
= 0.000000000

And dividing differences that are rounded to 0 is undefined, i.e. get the indeterminate form 0/0.

#InterestingStuff

mathematics calculus science messcience math stem education hiveeducation algebra tutorial
0
0
0.000
2 comments
avatar

Congratulations @mes! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :

You published more than 2000 posts. Your next target is to reach 2100 posts.

You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word STOP

Do not miss the last post from @hivebuzz:

October 2020 is the World Mental Heath Month
0
0
0.000
Reply