Infinite Sequences and Series: Kummer’s Test, Raabe’s Test, and Convergence of Binomial Series
In this video I go over more advanced tests for convergence in order to determine the convergence or divergence of the Binomial Series at the endpoints. In particular, I first derive Kummer’s Test, which is a generalization of both the Ratio Test, covered in my earlier video, and Raabe’s Test, which I cover in this video. I also show that Raabe’s Test is essentially a test that compares series to the p-series, which I had covered before.
In my earlier video, I had covered the Binomial Series and showed using the Ratio Test that the radius of convergence was less than 1 but the test was inconclusive at the endpoints. This is where I use Raabe’s Test to overcome the shortcomings of the Ratio Test and show that at the endpoints, the Binomial Series may converge or diverge depending on the value of k. This is a pretty epic and extensive proof video, and likely far more thorough than any other proof found online, so make sure to watch it!
Note that Kummer’s Test was first obtained by German mathematician Ernst Eduard Kummer, while Raabe’s Test was obtained by Swiss mathematician Joseph Ludwig Raabe, and both during the mid-1800s.
Also note, that I obtained the proofs for Kummer’s Test and Raabe’s Test from a paper by Sarah Fix from Whitman College, USA. As for the Binomial Series proof, I used mainly the lecture PDF by John Labute from McGill University, Canada.
The topics covered in this video are listed below with their time stamps.
- @ 1:29 - Topics to Cover
- @ 3:21 - Recap on the Ratio Test for Convergence
- @ 5:18 - Advanced Tests for Convergence
- @ 6:06 - Kummer's Test
- @ 36:02 - Ratio Test is Kummer's Test with Bn = 1
- @ 43:07 - Note on Kummer's Test
- @ 43:38 - Raabe's Test: Kummer's Test with Bn = n
- @ 51:45 - Raabe's Test Compares Series to the p-Series
- @ 1:02:05 - Corollary of Raabe's Test
- @ 1:23:01 - Note on Raabe's Test and Kummer's Test
- @ 6:06 - Kummer's Test
- @ 1:24:04 - Recap on Power Series
- @ 1:26:40 - Taylor and Maclaurin Series
- @ 1:27:32 - Recap on the Binomial Theorem
- @ 1:29:59 - Recap on the Binomial Series
- @ 1:32:32 - Convergence at the Endpoints Depends on the Value of k
- @ 1:34:48 - Important Note on the Binomial Coefficients
- @ 1:36:43 - Convergence of the Binomial Series
- @ 1:44:58 - Endpoint x = -1: Using Raabe's Test
- Converges when k > 0
- Diverges when k < 0
- @ 2:01:43 - Endpoint x = 1: Alternating Series
- @ 2:07:37 - Using Raabe's Test: Absolute Convergence when k > 0
- @ 2:12:34 - Using Alternating Series Test: Converges when -1 < k < 0
- @ 2:42:53 - Pi Production Notation for Factorials
- @ 2:48:14 - Using Comparison Test: Diverges when k ≤ -1
- @ 2:58:30 - Can Also Use the Test for Divergence
- @ 2:59:12 - Trivial Case k = 0: Converges for all x
- @ 2:59:29 - Summary
- @ 1:44:58 - Endpoint x = -1: Using Raabe's Test
Watch Video On:
- 3Speak: https://3speak.tv/watch?v=mes/cfcjcodb
- Odysee: https://odysee.com/@mes:8/1031-Kummer-Raade-Binomiol-Series-Convergence:2
- BitChute: https://www.bitchute.com/video/lsmOLZgcIHva/
- Rumble: https://rumble.com/v1rcb60-infinite-sequences-and-series-kummers-test-raabes-test-and-convergence-of-b.html
- DTube:
- YouTube: https://youtu.be/LOiRMhv6z8I
Download Video Notes: https://1drv.ms/b/s!As32ynv0LoaIiL4occLuFG9lN_2stg?e=jdv8Up
View Video Notes Below!
Download these notes: Link is in video description.
View these notes as an article: https://peakd.com/@mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate
Buy MES merchandise! https://mes.fm/store
More links: https://linktr.ee/matheasyReuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Recommended Books:
- "Where Did the Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Subscribe to MES Truth: https://mes.fm/truth
MES Links Telegram channel: https://t.me/meslinksJoin my forums!
- Hive community: https://peakd.com/c/hive-128780
- Reddit: https://reddit.com/r/AMAZINGMathStuff
- Discord: https://mes.fm/chatroom
Follow along my epic video series:
- #MESScience: https://mes.fm/science-playlist
- #MESExperiments: https://peakd.com/mesexperiments/@mes/list
- #AntiGravity: https://peakd.com/antigravity/@mes/series
-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept!- #FreeEnergy: https://mes.fm/freeenergy-playlist
- #PG (YouTube-deleted series): https://peakd.com/pg/@mes/videos
NOTE #1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial: https://peakd.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website- Download and read video notes.
- Read notes on the Hive blockchain #Hive
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations:
- Increase video speed: https://mes.fm/videospeed-extension
- Increase video audio: https://mes.fm/volume-extension
- Text to speech: https://mes.fm/speech-extension
--Android app: https://mes.fm/speech-android
Infinite Sequences and Series: Kummer's Test, Raabe's Test, and Convergence of Binomial Series

Calculus Book Reference
Note that I mainly follow along the following calculus book:
- Calculus: Early Transcendentals Sixth Edition by James Stewart
Topics to Cover
- Recap on the Ratio Test for Convergence
- Advanced Tests for Convergence
- Kummer's Test
- Ratio Test is Kummer's Test with Bn = 1
- Note on Kummer's Test
- Raabe's Test: Kummer's Test with Bn = n
- Raabe's Test Compares Series to the p-Series
- Corollary of Raabe's Test
- Note on Raabe's Test and Kummer's Test
- Kummer's Test
- Recap on Power Series
- Taylor and Maclaurin Series
- Recap on the Binomial Theorem
- Recap on the Binomial Series
- Convergence at the Endpoints Depends on the Value of k
- Important Note on the Binomial Coefficients
- Convergence of the Binomial Series
- Endpoint x = -1: Using Raabe's Test
- Converges when k > 0
- Diverges when k < 0
- Endpoint x = 1: Alternating Series
- Using Raabe's Test: Absolute Convergence when k > 0
- Using Alternating Series Test: Converges when -1 < k < 0
- Pi Production Notation for Factorials
- Using Comparison Test: Diverges when k ≤ -1
- Can Also Use the Test for Divergence
- Trivial Case k = 0: Converges for all x
- Summary
- Endpoint x = -1: Using Raabe's Test
Recap on the Ratio Test for Convergence
Recall from my earlier video in which I went over the Ratio Test to determine convergence of a series.
https://peakd.com/@mes/infinite-sequences-and-series-absolute-convergence-and-the-ratio-root-tests
Retrieved: 29 September 2020
Archive: https://archive.vn/wip/Cw0Oy



When the limit in the Ratio Test is equal to 1, the test is inconclusive thus we would need to conduct other tests to determine convergence.
Advanced Tests for Convergence
To go beyond the limitations of the Ratio Test, and other convergence tests that I had covered in my earlier videos, we will have to consider more "advanced" tests.
I will be going over the Kummer Test and the Raabe Test from the following very well written paper by Sarah Fix from Whitman College in Walla Walla, Washington State, USA.
https://www.whitman.edu/documents/Academics/Mathematics/2019/Fix-Gordon.pdf
Retrieved: 2 October 2020
Archive: https://web.archive.org/web/20200606232505/https://www.whitman.edu/documents/Academics/Mathematics/2019/Fix-Gordon.pdf
Local PDF download: https://1drv.ms/b/s!As32ynv0LoaIiL1MaqSTZlFh95e2vw?e=kLCwuIAdvanced Tests for Convergence
Sarah Fix
May 8, 2019
The first convergence test I will go over is Kummer's Test and which was developed by the German mathematician Ernst Eduard Kummer (29 January 1810 – 14 May 1893).
Kummer's Test
Let ∑∞n=1 an be a series of positive terms and let {Bn} be as sequence of positive constants.
Assume that the following limit exists (is a finite value):
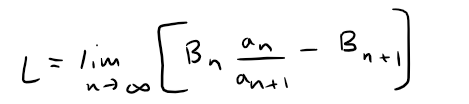
(i) If L > 0, then the series ∑ an converges.
(ii) If L < 0 and **∑∞n=1 1/Bn diverges then the series ∑∞n=1 an diverges.
Proof:
We begin considering the case where L > 0.
Choose a number r such that 0 < r < L.
Then there must exist some integer N > 0 such that, for all n ≥ N:
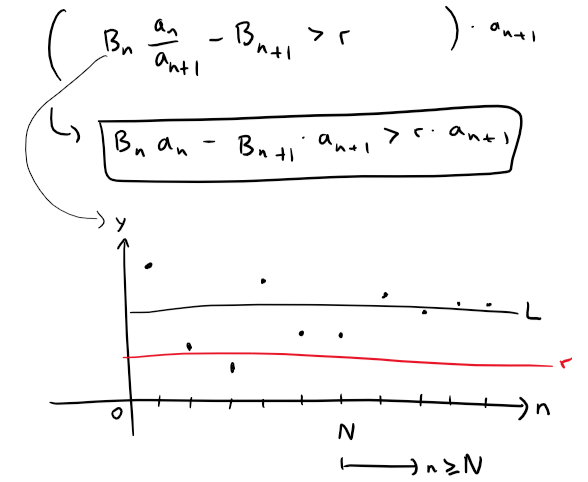
Given any positive integer m, and starting from n = N, we have:
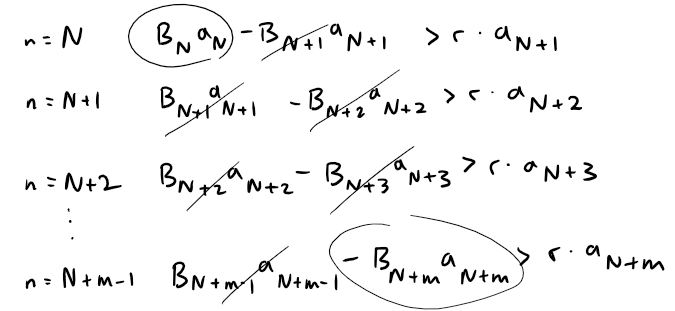
And then adding these inequalities together, we get cancellations of all of the terms on the left side of the inequality except the first and last; thus we have:
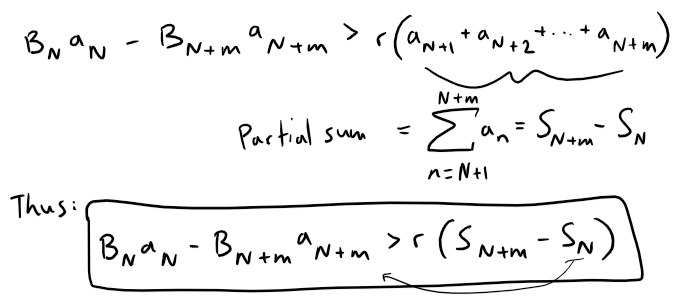
It follows that:

Thus, the sequence of the partial sums {Sn} of the series ∑∞n=1 an is bounded, and increasing (because all of the terms are positive), and therefore the series converges by the Monotonic Sequence Theorem referenced below from my earlier video.
Retrieved: 9 October 2020
Archive: https://archive.vn/wip/BQQuH



Essentially, if a sequence is always increasing (or decreasing), hence monotonic, and is bounded above (or below) then it will approach a number or limit L ≤ M (or L ≥ m if the sequence is decreasing).

Now let's consider the case where L < 0.
This means that there exists an integer N > 0 such that, for all n ≥ N:
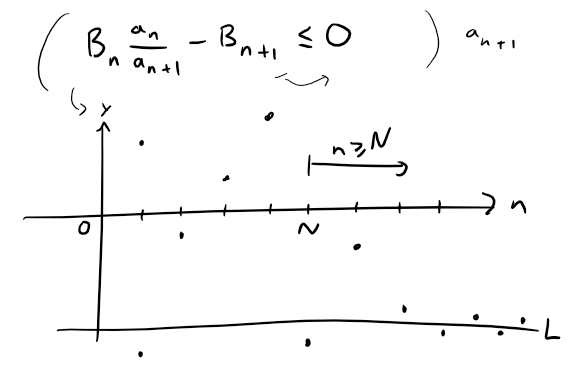
Rearranging this inequality gives us:
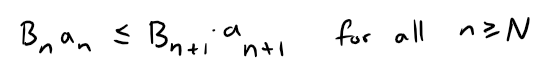
This implies that:
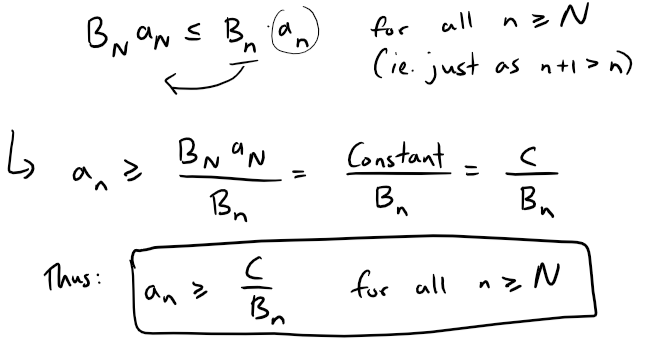
Since we are given the ∑∞n=1 1/Bn diverges then the series ∑∞n=1 an diverges by the Comparison Test, referenced below from my earlier video.
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-the-comparison-tests
Retrieved: 3 October 2020
Archive: https://archive.vn/wip/WWa1E

Ratio Test is Kummer's Test with Bn = 1
Using Kummer's Test, if we let the sequence {Bn} = {1}, then we get:
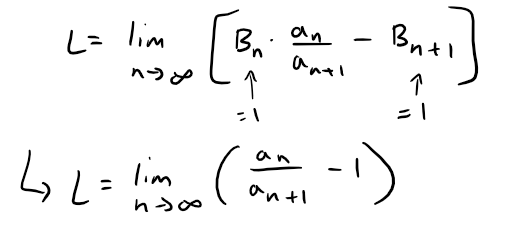
If the limit of the ratio is greater than 1 then L is positive:
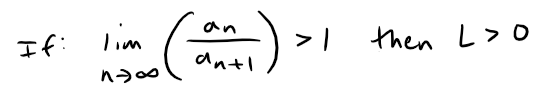
Thus the series converges by Kummer's Test.
And inverting the ratio we get:

Thus this series also converges by the Ratio Test.
https://peakd.com/@mes/infinite-sequences-and-series-absolute-convergence-and-the-ratio-root-tests

Similarly, if the limit of the ratio in Kummer's Test is less than 1 then L is negative.
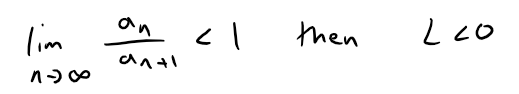
Thus the series diverges by Kummer's Test.
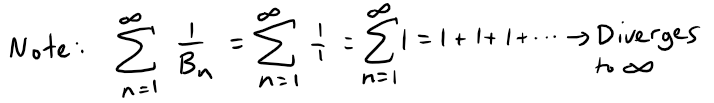
And the inversion of this limit yields:
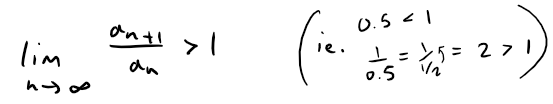
Likewise, this series diverges by the Ratio Test.
Therefore, we can conclude that the Ratio Test is simply Kummer's Test associated with the sequence {Bn} = {1}.
Note on Kummer's Test
Kummer's Test is inconclusive when L = 0, but when this happens it is possible to refine the sequence {Bn} to give a result, which is why the case when L = 0 is not included in the definition of the test.
But because there is no specific strategy for choosing {Bn} this can become a tedious and time-consuming task in order to find a sequence that yields a result when used in Kummer's Test.
This is where Raabe's Test comes in.
Raabe's Test is simply a specific case of Kummer's Test where we let Bn = n, therefore we do not have to go through the process of trying to find a suitable Bn.
Raabe's Test was formulated by the Swiss mathematician Joseph Ludwig Raabe (15 May 1801 to 22 January 1859) and is stated below.
Raabe's Test: Kummer's Test with Bn = n
Let ∑∞n=1 an be a series with positive terms and assume that the following limit exists (is finite):
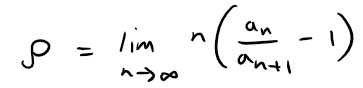
(i) If ρ > 1, then the series ∑∞n=1 an converges.
(ii) If ρ < 1, then the series ∑∞n=1 an diverges.
(iii) If ρ = 1, then ∑∞n=1 an may either converge or diverge and the test is inconclusive.
MES Note: ρ is the Greek letter "rho".
Proof:
Parts (i) and (ii) are consequences of Kummer's Test.
To demonstrate this, let Bn = n and compute:

If ρ > 1, then L > 0 and the series ∑∞n=1 an converges by Kummer's Test.
Similarly, if ρ < 1, then L < 0 and recall that **∑∞n=1 1/Bn = ∑∞n=1 1/n diverges as referenced below, thus the series ∑∞n=1 an diverges by Kummer's Test.
https://peakd.com/@mes/infinite-sequences-and-series-the-integral-test-and-estimate-of-sums
Retrieved: 3 October 2020
Archive: https://archive.vn/wip/Kb8Sn
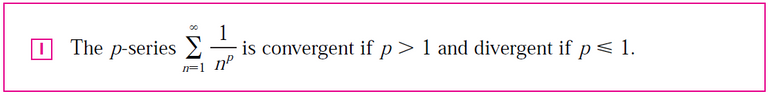
Note that when p = 1, it is often called the harmonic series.
If the result of Raabe's Test is ρ = 1, then the test is inconclusive.
Raabe's Test Compares Series to the p-Series
Applying Raabe's Test to the p-series gives us:
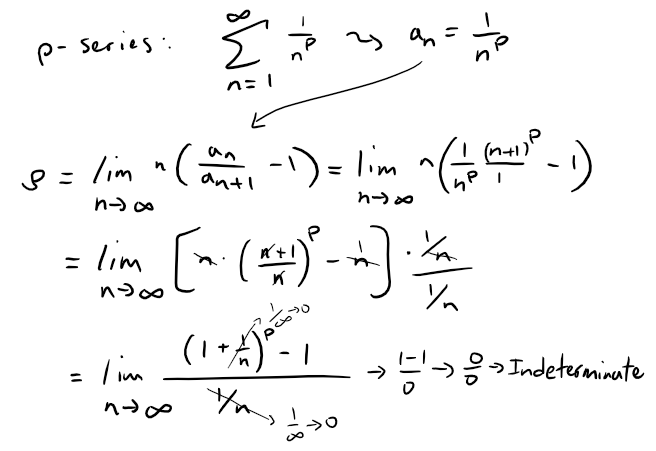
Recall L'Hospital's Rule for evaluating "indeterminate" limits.
Retrieved: 3 October 2020
Video notes archive: https://archive.vn/qiZ5r

Thus the limit becomes:

Thus, if ρ > 1, then the series converges by Raabe's Test.
This implies that p > 1 which indicates that the series is a convergent p-series.
On the other hand, if ρ < 1 then we know the series diverges by Raabe's Test, and this implies that p < 1 and therefore the series is a divergent p-series.
This demonstrates that Raabe's Test tests a series for convergence by comparing the series to the p-series where p = ρ.
Corollary of Raabe's Test
In general, when ρ > 0, the sequence {an} converges to 0.
MES Note: Corollary means a proposition or statement that directly follows from one that already proved.
Proof
When ρ > 0, there must exist some integer M such that, for all n ≥ M:
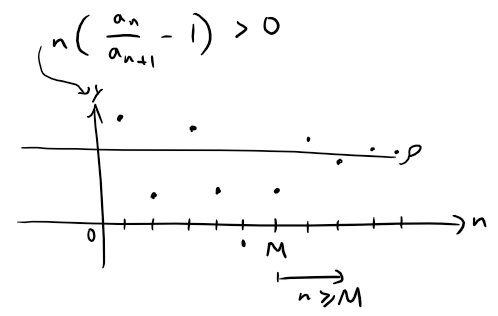
It follows that:
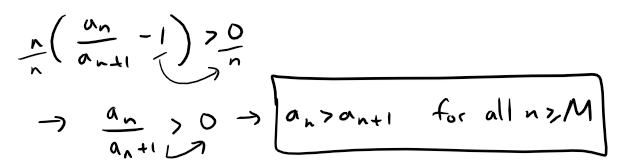
This tells us that {an is eventually decreasing, therefore {an converges to some number L.
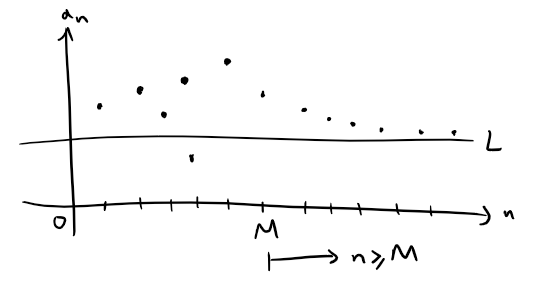
To show that L = 0, we use proof by contradiction and assume L > 0.
Similar to our above reasoning, because ρ > 0 there exists some integer N and a number ϵ > 0 such that, for all n ≥ N:
MES Note: ϵ is the Greek letter "epsilon".

From this, we see that:
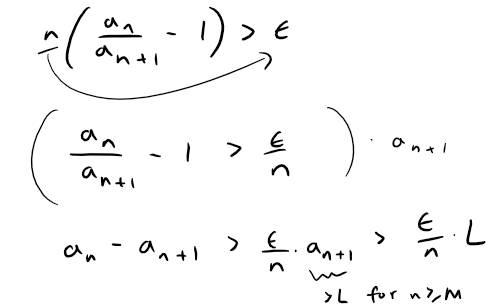
Now, "telescoping" (again) this difference gives us, whenever m > n ≥ N.
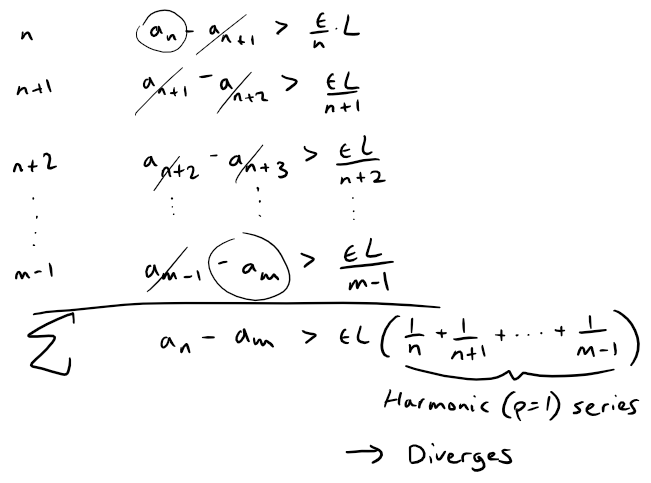
Since the sequence of partials sums for the harmonic series (p = 1 series) diverges and we know that {an converges, we have reached a contradiction.
Therefore, the sequence {an} converges to 0, that is L = 0.

Thus, we have proved the corollary.
Note on Raabe's Test and Kummer's Test
Raabe and Kummer had worked on power series at about the same time during the mid-1800s.
But it was Raabe's Test that chronologically preceded Kummer's Test, so instead of considering Raabe's Test to be a refinement of Kummer's Test, we could also consider Kummer's Test to be a generalized version of Raabe's Test.
Recap on Power Series
Here is a recap of power series, which are a specific type of series.
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-power-series
Retrieved: 6 August 2020
Archive: https://archive.vn/mpruy
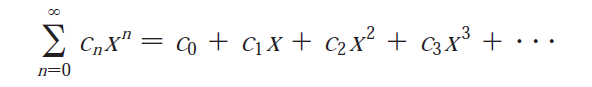
Power series centered at a:
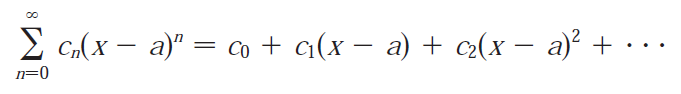
The convention (x - a)0 = 1 is used even when x = a.

Note that R is the radius of convergence; R = a for (i) and R = ∞ for (ii).
When |x - a| = R then the series may converge or may diverge, i.e. at the endpoints of the interval of convergence x = a ± R.
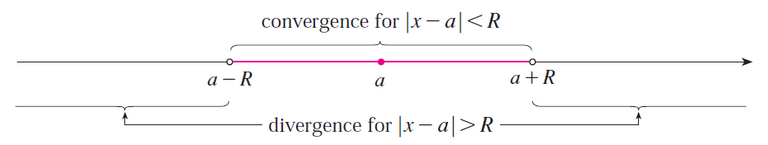
Taylor and Maclaurin Series
Recall that the Taylor series is just a power series in which the coefficients are determined from the function's derivatives.
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-taylor-and-maclaurin-series
Retrieved: 24 September 2020
Archive: https://archive.is/w3n31

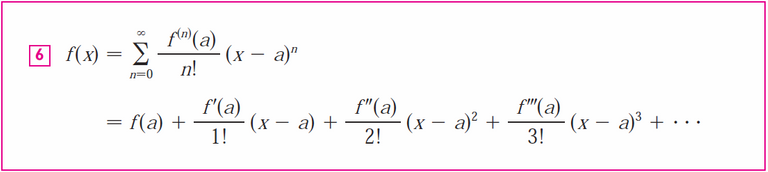
The Maclaurin series is a just a specific type of Taylor series with a = 0:
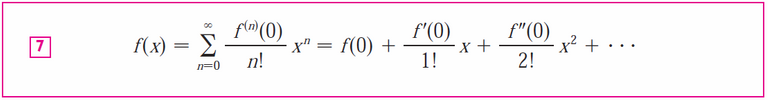
Recap on the Binomial Theorem
The binomial theorem (or binomial expansion) is the algebraic expansion the powers of a binomial, that is a polynomial consisting of just two terms or two monomials.
https://peakd.com/@mes/infinite-sequences-and-series-representations-of-functions-as-power-series
Retrieved: 6 August 2020
Archive: https://archive.vn/wip/JsH4l
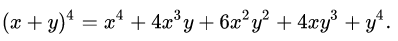

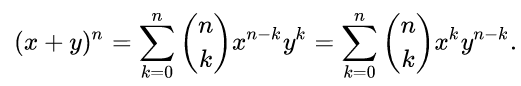
The term (nk) are the binomial coefficients and often pronounced "n choose k".
They can be determined in factorial form or via Pascal's triangle in which each entry is the sum of the two above it.


Recap on the Binomial Series
Recall that the binomial series is just the Maclaurin series for the function (1 + x)k.
In my earlier video I went over the derivation of the Binomial series and used the Ratio Test to determine that its interval of convergence is |x| < 1.
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-taylor-and-maclaurin-series
Retrieved: 5 October 2020
Archive: https://archive.vn/wip/Fkkz7


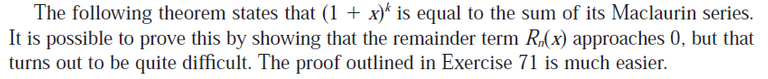
MES Note: I solved the proof in Exercise 3.

Convergence at the Endpoints Depends on the Value of k:

MES Note: It reduces to the ordinary Binomial Theorem with y = 1.
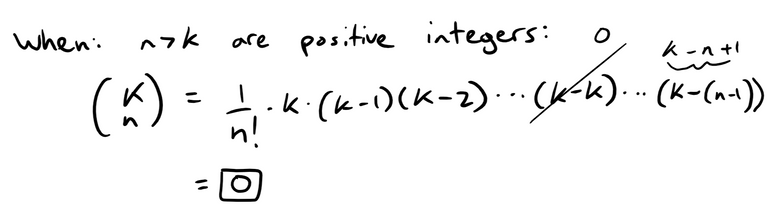
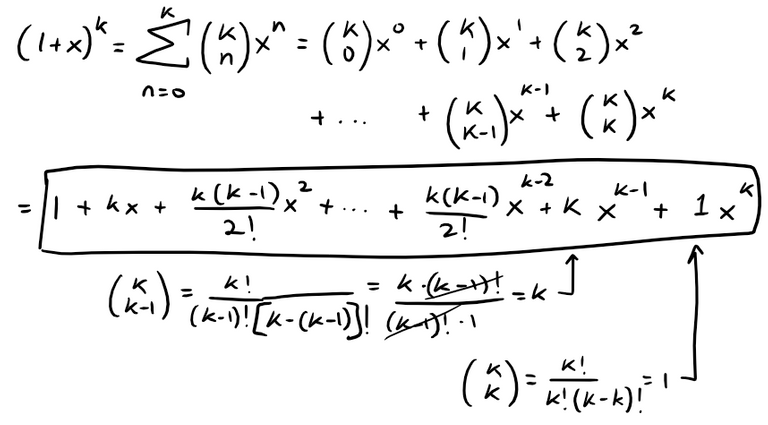
Important Note on the Binomial Coefficients
The binomial series is defined for when k is any real number and thus the binomial coefficients are written in the more general version below:
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-taylor-and-maclaurin-series
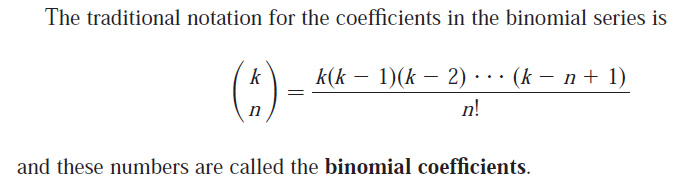
But if k is a positive integer, where k > n, then it is equivalent to the usual factorial form present in the binomial theorem.
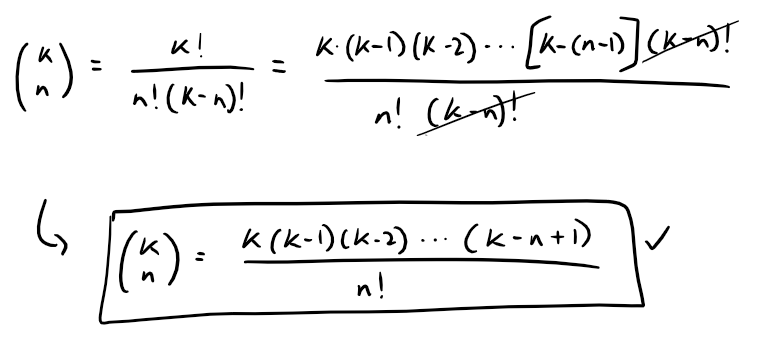
Note also that the terminology for the binomial coefficient is usually reversed for considering the binomial series vs. the binomial theorem.
Binomial series:
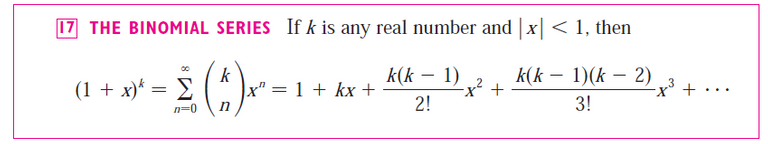
Binomial theorem:
https://peakd.com/@mes/infinite-sequences-and-series-representations-of-functions-as-power-series
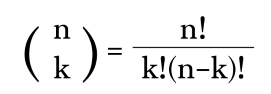
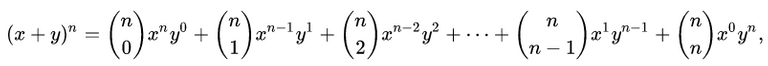
Convergence of the Binomial Series
I will be using the following PDF for the proof of the convergence at the end points for the binomial series.
It is by mathematics professor John Labute from McGill University in Montreal, Quebec, Canada.
MES Note: Unlike the very well written paper by Sarah Fix, this particular lecture PDF by John Labute was painfully hard to follow and much of the proof was skipped through.
https://www.math.mcgill.ca/labute/courses/255w03/L22.pdf
Retrieved: 1 October 2020
Archive: https://web.archive.org/web/20190819021224/http://www.math.mcgill.ca/labute/courses/255w03/L22.pdf
Local archive: https://1drv.ms/b/s!As32ynv0LoaIiIElPbnLoio_C3fWrA?e=Ghp92sMATH 255: Lecture 22
Power Series: The Binomial Series
MES Note: I will be using the term k instead of the α term used in the PDF lecture.
The binomial series is the Maclaurin power series for the function f(x) = (1 + x)k and is equal to f(x), that is:
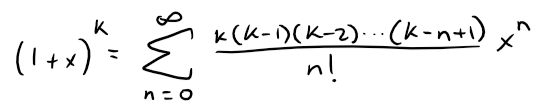
Let's go over the Ratio Test again, for completeness, to determine the radius of convergence.
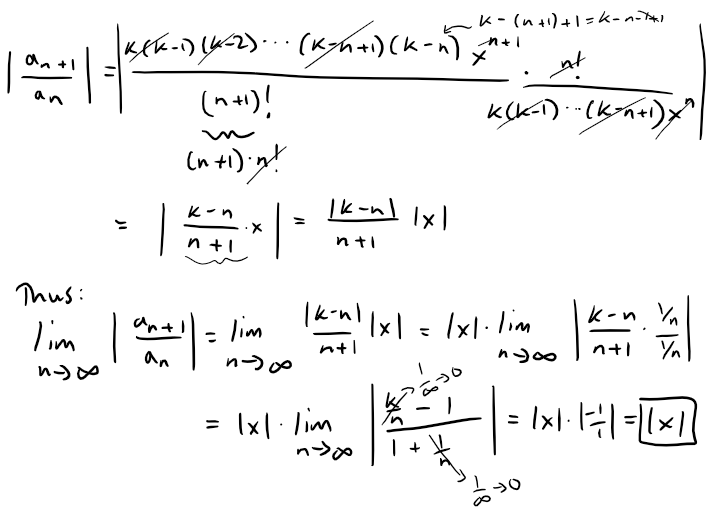
Thus, by the Ratio Test, the binomial series converges if |x| < 1 and diverges if |x| > 1.
Endpoint x = -1: Using Raabe's Test: Converges when k > 0 and Diverges when k < 0
When x = - 1 (or +1), the Ratio Test is equal to 1 and is thus inconclusive.

This is where we can use Raabe's Test discussed earlier and shown below:
https://www.whitman.edu/documents/Academics/Mathematics/2019/Fix-Gordon.pdf

When x = -1 and n > k, the sequence {an has a constant sign, thus we can apply Raabe's test.
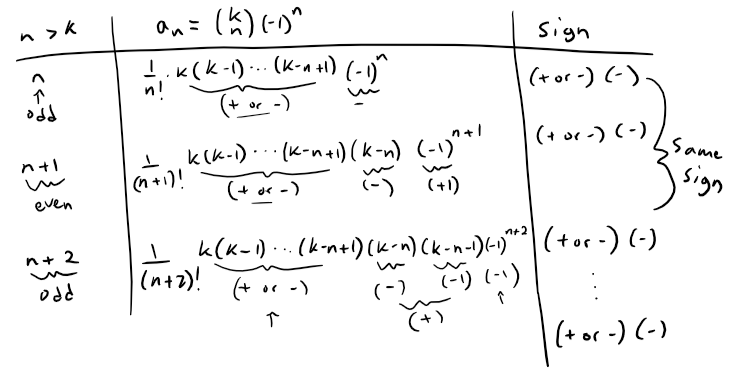
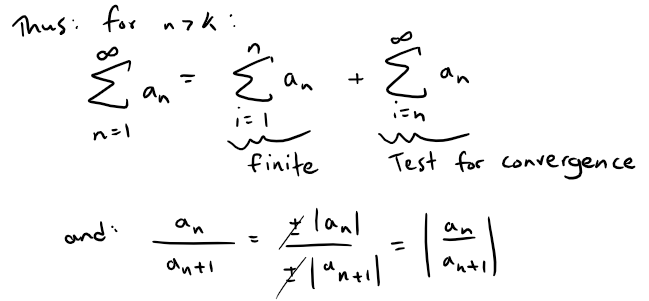
Applying Raabe's Test, and recalling the earlier derived ratio from the Ratio Test, we have:

Thus at the endpoint x = -1, the binomial series converges when k > 0 and diverges when k < 0.
Endpoint: x = 1: Alternating Series
If x = 1, the binomial series becomes alternating for n > k.

Using Raabe's Test: Absolute Convergence when k > 0
Since the series is an alternating series, we can nonetheless consider absolute convergence using Raabe's Test:
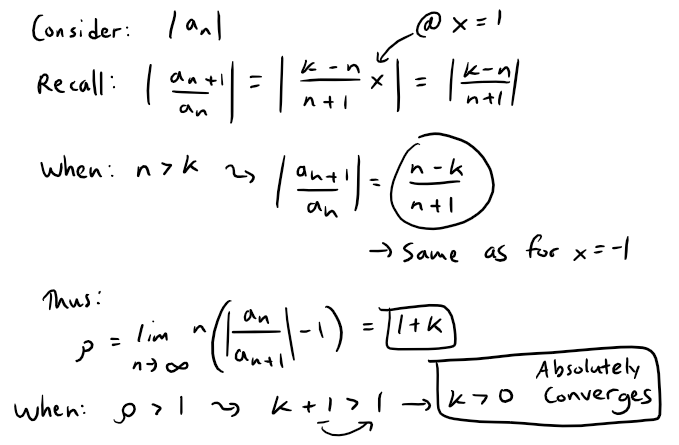
Thus by Raabe's Test, at the endpoint x = 1, the binomial series absolutely converges, and therefore converges, when k > 0.
Using Alternating Series Test: Converges when - 1 < k < 0
Note that we can't use the Raabe's test to check for divergence of the alternating series since absolute divergence does not necessarily mean divergence.
This is where we can apply the Alternating Series Test from my earlier video.
https://peakd.com/@mes/infinite-sequences-and-series-alternating-tests
Retrieved: 6 October 2020
Archive: https://archive.vn/wip/DDec8

In our case, at the endpoint x = 1 and when n > k, the series is alternating and we need to determine convergence when k < 0.
When -1 < k < 0, then:
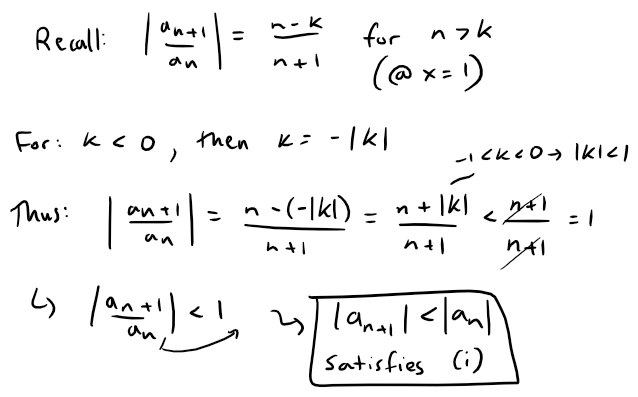
Thus the first condition |an+1| < |an| of the Alternating Series Test is satisfied so that we only have to show that |an| → 0 (and hence an → 0).
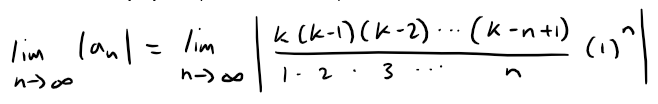
It is not clear how to determine the limit of this function but we can try converting this factorial multiplication into logarithmic summation, which often simplifies the equation, using the logarithms laws that I had covered in one of my earliest videos.
Retrieved: 7 October 2020
Archive: https://archive.vn/wip/F6LSV
Thus, taking the limit of the (natural) logarithm of the sequence |an|, we get:
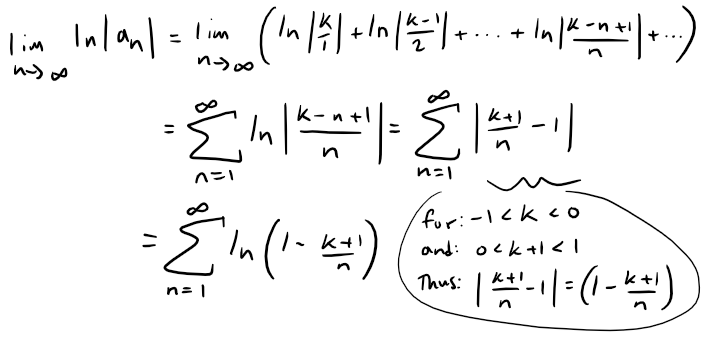
Thus the limit of the natural log of the sequence |an| is equal to the above series, #InteresetingStuff.
Note that the PDF lecture proof is not clear and skips most of their steps, so instead we will test for convergence or divergence of the series by the Limit Comparison Test also covered in my earlier video.
https://peakd.com/mathematics/@mes/infinite-sequences-and-series-the-comparison-tests
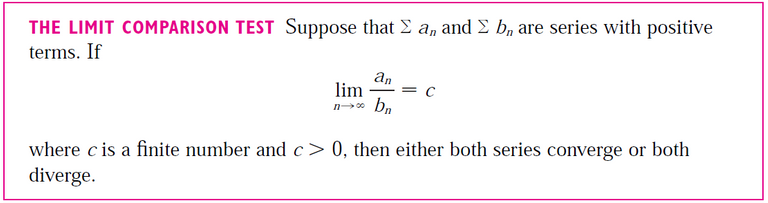
Note that in our case, our logarithmic series is always < 0 but this just means we have to ensure that bn is negative for all terms as well; like before, all that matters is that the sign for each term is the same as n → ∞ so that we aren't dealing with an alternating series.
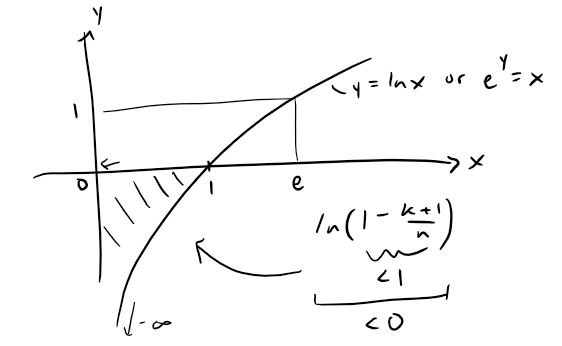
Setting u = k + 1 and choosing bn = -u/n, we can apply the Limit Comparison Test.
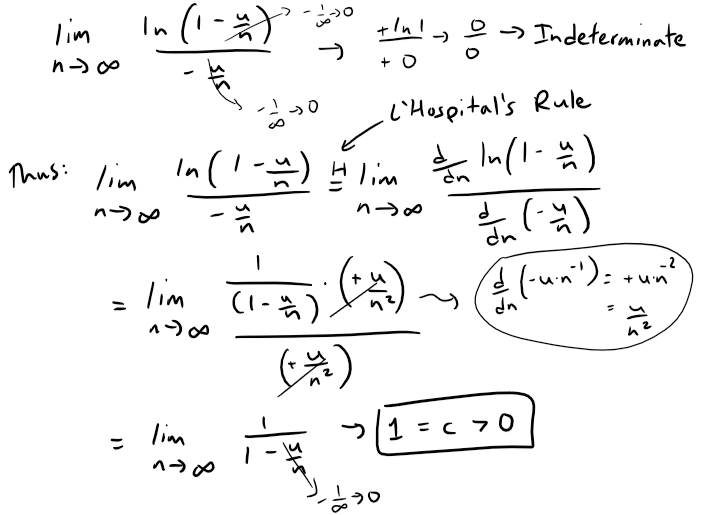
Since the limit is finite and greater than zero, we now just need to determine the convergence of ∑ bn, which in our case is just a constant multiple of the harmonic (p = 1) series, which diverges.
This means that our natural log series also diverges by the Limit Comparison Test.

Thus, by the Alternating Series Test, the binomial series converges for -1 < k < 0 at the endpoint x = 1.
Pi Product Notation for Factorials
Note that we can write the sequence an in "pi product notation" and which is a more generalized notation for the factorial function.
https://en.wikipedia.org/wiki/Factorial
Retrieved: 7 October 2020
Archive: https://archive.vn/wip/aCS4tThe factorial function is defined by the product
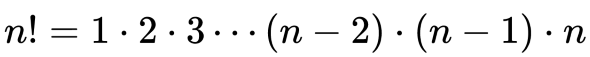
for integer n ≥ 1. This may be written in pi product notation as

Thus our sequence |an| becomes:
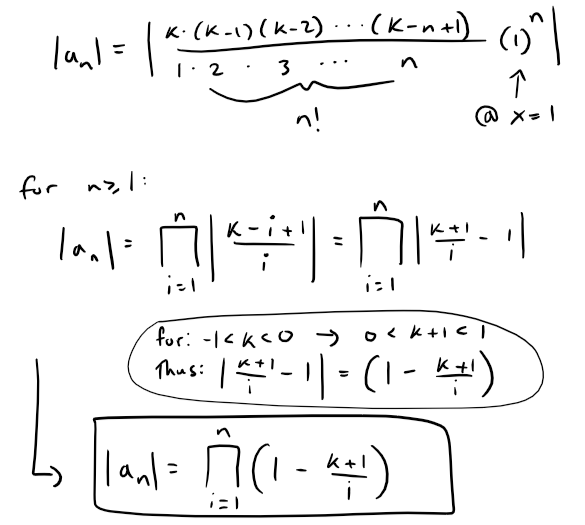
Using Comparison Test: Diverges when k ≤ -1
Starting back from our earlier absolute value ratio, at x = 1 and when k ≤ -1, we have:
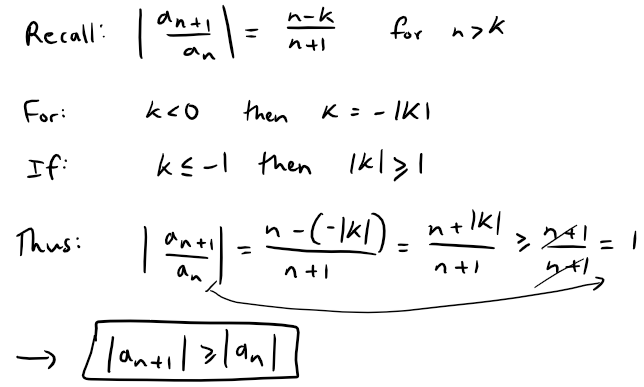
Note that this doesn't meet condition (i) in the Alternating Series Test, so we must use a different method.
MES Important Note: The Alternating Series Test does not explicitly state a series is divergent if the test's criteria are not met for convergence.
Nonetheless, I have not seen any scenario in which a series converges while the terms are increasing, that is when |an+1| > |an|.
In our case we can see that |an| ≥ 1 thus we can use the Comparison Test as follows:
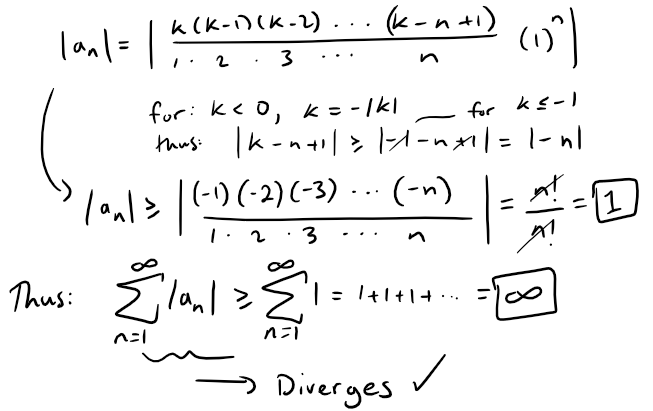
Note that we could have also used the Test for Divergence from my earlier video since |an| does not approach 0 as n → ∞.
https://peakd.com/@mes/infinite-series-definition-examples-geometric-series-harmonics-series-telescoping-sum-more
Retrieved: 8 October 2020
Archive: https://archive.vn/wip/RN1oe
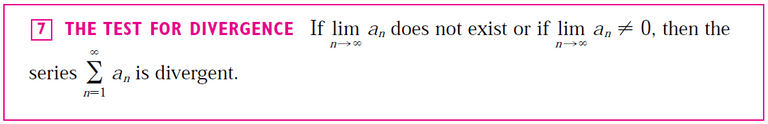
Trivial Case k = 0: Converges for all x
When k = 0, the binomial series reduces to 1 by convention.
Summary
The Binomial Series:
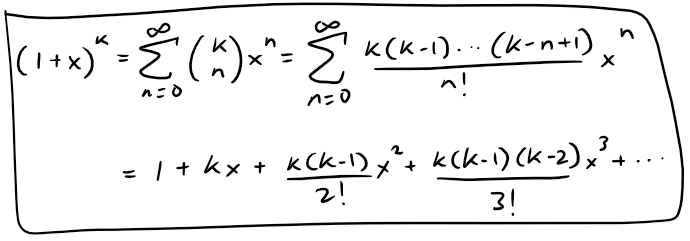
Converges on the following interval of convergence I, depending on the value of the real number k:
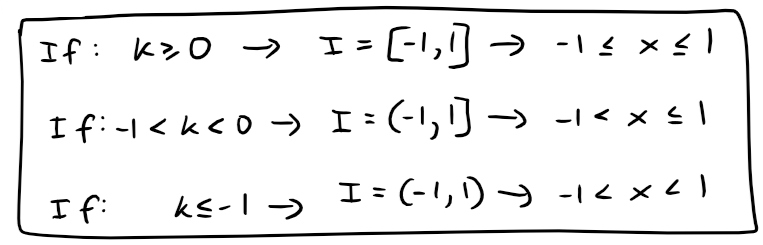
MES Note: This video took a lot of energy out of me in the making of it haha =P
https://twitter.com/MathEasySolns/status/1316114843649277953